反三角函数讲座
主题: 反三角函数
摘要
在这次讲座中,我将介绍反三角函数的概念:arcsinx, arccosx, arctgx, arcctgx。它们是三角函数的反函数。
讲座分为两个部分。第一部分我只是快速讲解如何计算反三角函数的值,不会深入探讨(这一部分附有视频,是我积分课程的一部分)。
第二部分我会更详细地描述反三角函数,展示它们的图像等等。
理解讲座需要具备以下知识:
- 三角函数(高中)
第一部分
反三角函数 – “速成版”
反三角函数简单来说就是三角函数的反函数。也就是说,arcsinx 是 sinx 的反函数。
所以如果我们知道 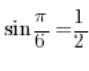 ,那就意味着
,那就意味着 ![]() 。
。
依此类推:
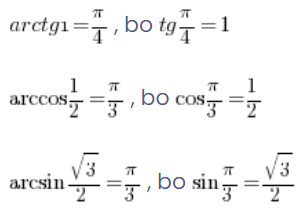
我们还有一些反三角函数的特性,这些特性使我们能够计算负数的值:
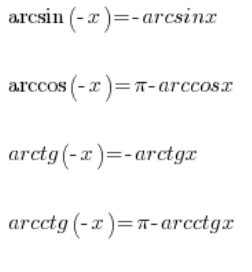
所以我们可以再计算这个:
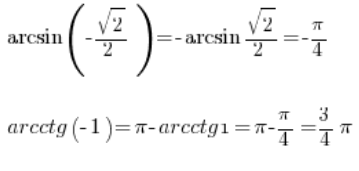
因此,有了三角函数表,我们可以从中轻松确定反三角函数的值,只需反过来读取即可。
我在视频中详细解释了这一点:
视频中的三角函数基本值表 – 下载这里。
第二部分
反三角函数 – 完整版
引言 – 为什么第一部分还不够
看起来在第一部分中,我们将每个反三角函数定义为对应三角函数的反函数。
让我们正式一点。我们说,例如,函数 ![]() 取值
取值 ![]() ,当函数
,当函数 ![]() 从
从 ![]() 得到的值为
得到的值为 ![]() 。
。
同样地:
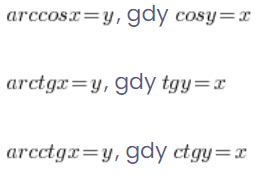
也就是说,如果我们想计算 ![]() ,我们会想,哪个角度的余弦是
,我们会想,哪个角度的余弦是 ![]() ,然后得出这个角度是
,然后得出这个角度是 ![]() ,结果是:
,结果是: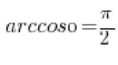 。
。
这就涵盖了反三角函数的所有值吗?
当然不是。
让我们再用具体的数字重新推导一下(也许传统地换到 arcsinx 上):
如果我们想计算  ,我们会想,哪个角度的正弦是
,我们会想,哪个角度的正弦是 ![]() ,然后得出这个角度是
,然后得出这个角度是 ![]() ,结果是:
,结果是: 。
。
问题出在哪里?在加粗的部分:
如果我们想计算  ,我们会想,哪个角度的正弦是
,我们会想,哪个角度的正弦是 ![]() ,然后得出这个角度是
,然后得出这个角度是 ![]() ,结果是:
,结果是: 。
。
不幸的是,不仅仅是角度 ![]() 的正弦等于
的正弦等于 ![]() 。
。
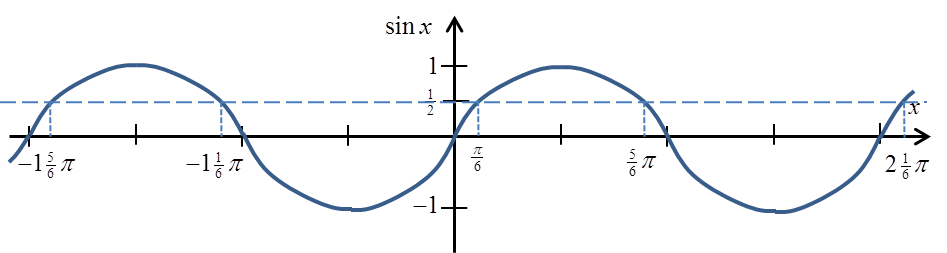
让我们回顾一下 sinx 的图像(我在图上标出了值 ![]() ):
):
我们知道并且在高中学过,正弦值为 ![]() 不仅在角度
不仅在角度 ![]() ,还有角度:
,还有角度: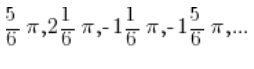
也就是说 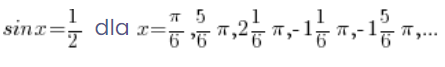
让我们再次回顾一下计算 arcsin 的方法:
如果我们想计算  ,我们会想,哪个角度的正弦是
,我们会想,哪个角度的正弦是 ![]() ,然后得出这个角度是
,然后得出这个角度是 ![]() ,结果是:
,结果是: 。
。
但现在我们已经知道,不只是 sin![]() 等于
等于 ![]() ,所以看起来:
,所以看起来:
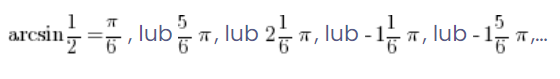
这意味着 arcsinx 根本不是函数,因为一个自变量对应多个值!
如果是这样的话,就无法给出 arcsin 某个值的明确答案。
我们也很容易想象,类似的问题适用于所有三角函数。
更专业地说,这些函数不是单值函数,因此它们的逆函数不存在。对于每个三角函数,每个值都有无限多个自变量(它们是周期性的,对吗?),因此在尝试求出它们的逆函数时,每个自变量都会有无限多个对应值。而函数不可能这样。
怎么办?
这相当简单,如果不说粗陋的话。可以剪切每个三角函数,从而得到一个单值函数。
那么,让我们正确地定义所有 4 个反三角函数:
arcsinx
回顾一下 sinx 的图像:
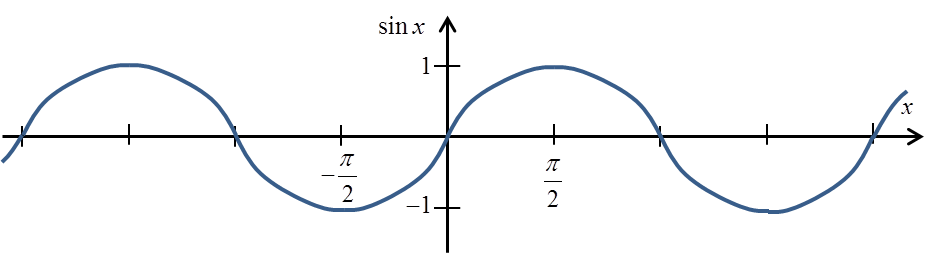
如果我们约定将其剪切到 ![]() 区间,我们将得到这样的图像:
区间,我们将得到这样的图像:
![Wykres sinx w przedziale [0,pi] Obraz3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
不幸的是,这不是我们想要的,因为它仍然不是单值函数的图像,并且 ![]() 的问题仍然存在:
的问题仍然存在:
![Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2 Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
因此,我们同意将 sinx 函数剪切到 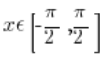 区间:
区间:
![Wykres funkcji sinx dla x należących do [-pi/2,pi/2] Wykres funkcji sinx dla x należących do [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
现在这是一个单值函数,并且有它的反函数 arcsinx。
arcsinx 的图像大致如下:

它的定义域是 ![]() 不存在。
不存在。
因此,arcsinx 的精确定义是:
![]() 。
。
arccosx
cosx 函数也不是单值函数:
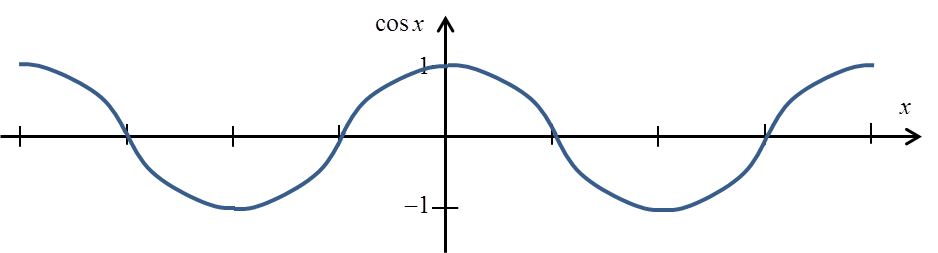
要得到单值函数,我们必须将其剪切到 ![]() 区间:
区间:
![Wykres funkcji cosx obciętej do przedziału [0,pi] Wykres funkcji cosx obciętej do przedziału [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
这样定义的函数是单值的,并且有反函数 arccosx。
它的图像大致如下:
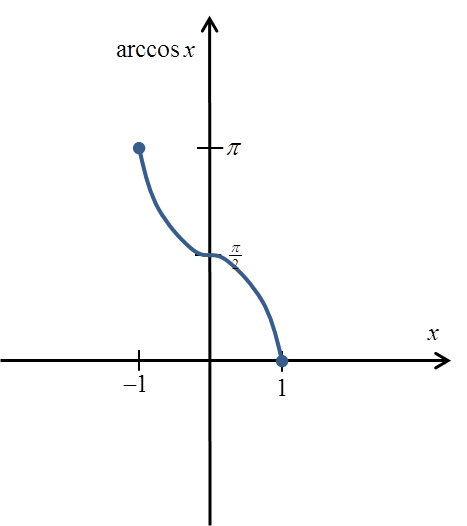
它的精确定义是:
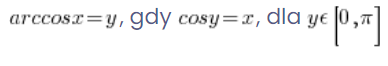 。
。
arctgx
tgx 函数的图像如下:

这也不是单值函数!我们可以将其剪切如下:
![Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2] Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
这样我们就得到了单值函数。
arctgx 函数的图像如下:

它的精确定义是:
![]() ,对于 y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right)。
,对于 y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right)。
我们还注意到,从图像中可以看出一些有趣的性质,例如:
- arctgx 函数的定义域是整个实数集(我们可以计算任何数的 arctg)


arcctgx
从 ctgx 函数的图像:

我们剪切出单值部分:
arcctgx 函数的图像如下:
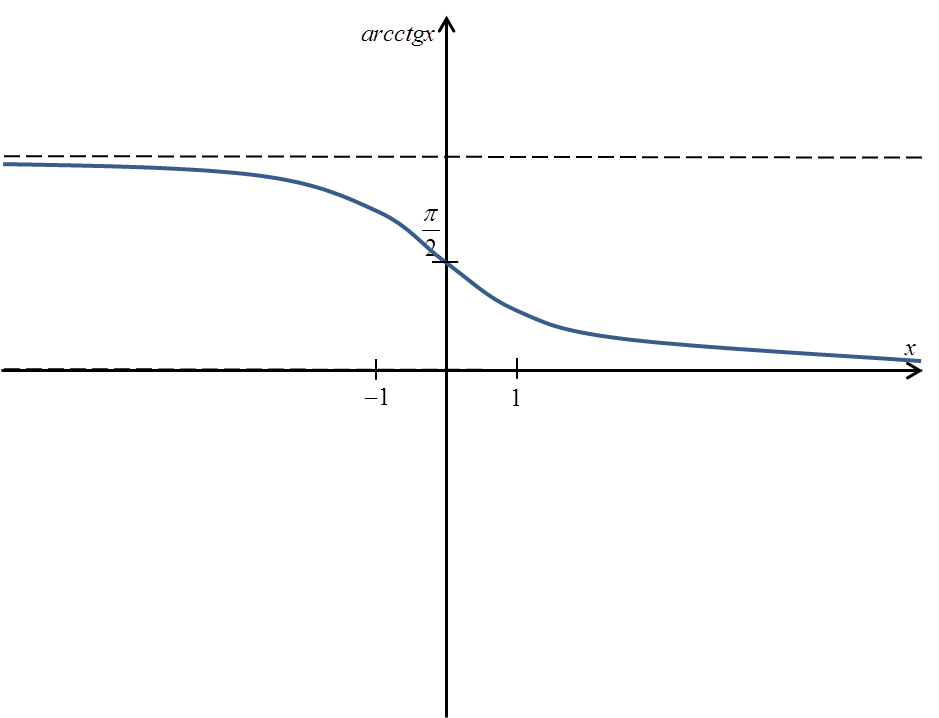
arcctgx 的精确定义是:
![]() 。
。
可以看到:
- arcctgx 函数的定义域是整个实数集(我们可以计算任何数的 arcctg)


注意
在许多计算器和一般数学表示法(尤其是西方)中,逆三角函数不是用“arcus”表示,而是用指数 -1。例如,arcsinx 写作 ![]() 。如果知道这是什么意思,就没有问题。但是可能会犯一个严重的错误,将 sinx 的逆函数与
。如果知道这是什么意思,就没有问题。但是可能会犯一个严重的错误,将 sinx 的逆函数与 ![]() 函数混淆 – 它与 arcsinx 是完全不同的函数。
函数混淆 – 它与 arcsinx 是完全不同的函数。