![]() 计算上面方程组中参数 ‘a’,已知它是矛盾的。
计算上面方程组中参数 ‘a’,已知它是矛盾的。
与其 系统地 开始计算主矩阵的 秩,我们来确定增广矩阵的 秩:
![]() …它等于二,因为在这个矩阵中可以提取出一个非零的二阶 行列式(更大的就不行了):
…它等于二,因为在这个矩阵中可以提取出一个非零的二阶 行列式(更大的就不行了):
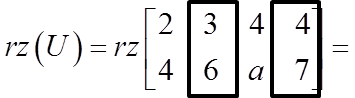
![]() 所以增广矩阵的秩等于2。
所以增广矩阵的秩等于2。
克罗内克-卡佩利定理的应用
那么主矩阵的秩应该是多少?
我们知道该方程组是矛盾的,根据 克罗内克-卡佩利定理 我们知道,当主矩阵的秩与增广矩阵的秩不同时,方程组是矛盾的。我们还知道,主矩阵的秩总是小于或等于增广矩阵的秩(主矩阵包含在增广矩阵中)。因此,主矩阵的秩应该是1或0(与增广矩阵的秩不同)。
主矩阵的秩为:
![]() 我们看到它绝对不会等于0(只有零矩阵的秩才等于0) – 因此它应该等于1。当第一行和第二行成比例时,秩将等于1(然后我们会删除其中一行)。可以看到,当a等于8时,第一行乘以二等于第二行。
我们看到它绝对不会等于0(只有零矩阵的秩才等于0) – 因此它应该等于1。当第一行和第二行成比例时,秩将等于1(然后我们会删除其中一行)。可以看到,当a等于8时,第一行乘以二等于第二行。
所以很快且无需大计算我们得出答案:
![]()


