函数极值 第7讲
主题：函数极值存在的充分条件（导数符号的变化）。
摘要
就像我们在上一讲中发现的，仅仅因为函数的导数在某点等于0，并不意味着该函数在这点达到极值。所以，我们在这里将讨论什么条件足够一个函数在某点达到极值。
极值存在的充分条件
假设在点 x_0 的某个邻域内，函数 f \left(x \right) 有有限导数 f' \left( x \right)：
- 如果在这个邻域内 x_0 的左侧导数值为正，右侧为负 – 那么 函数在点 x_0 处取得最大值
- 如果在这个邻域内 x_0 的左侧导数值为负，右侧为正 – 那么 函数在点 x_0 处取得最小值
实际上，根据上一讲中介绍的函数单调性引理，如果函数的导数
取正值，这意味着函数
是增加的。如果导数取负值，那么意味着函数是减少的。
因此，如果导数“变号”，这也意味着函数的单调性发生了变化，例如在情况1中：
导数在 
左边是正的，在右边是负的。这意味着函数 在 的左侧上升，在右侧下降。所以应该是这样的：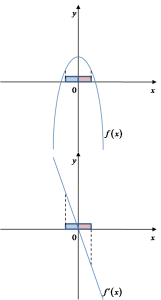
在上面的图表中，我们有函数 
（顶部）及其导数 
的图表。可以看到，在 
的“左侧”区域（标蓝）导数 是正的，函数 在增加。在 的“右侧”区域（标红）导数 是负的，函数 在减少。
这种变化总是意味着在 点存在一个最大值。
结束
编写此帖子时，我参考了…
1. “微分和积分计算。第一卷。” G.M. Fichtenholz。1966年版。