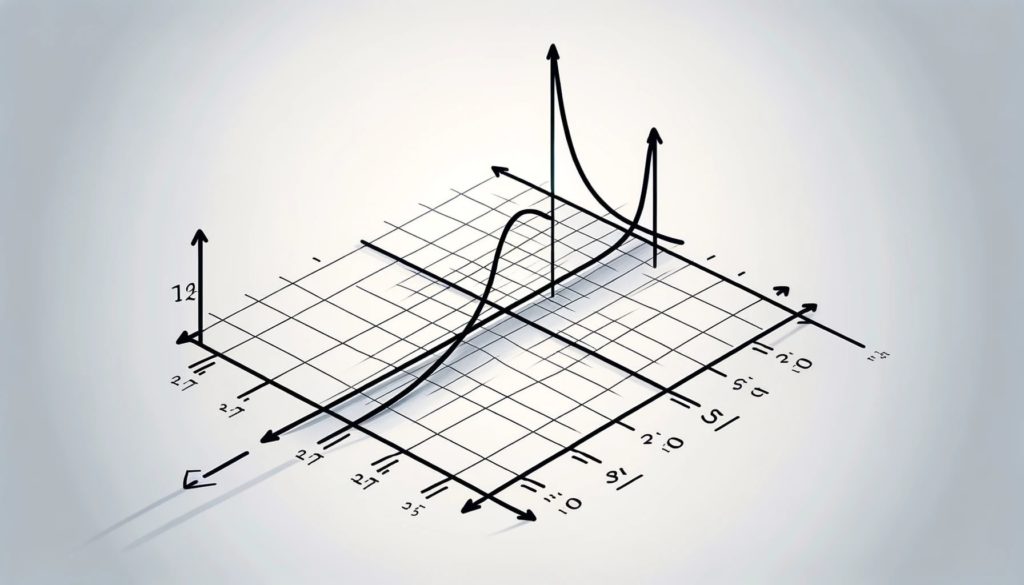
函数的水平和斜渐近线之间的关系如下:水平渐近线是特殊的斜渐近线。也就是说,每一个水平渐近线也是斜渐近线,但并不是每个斜渐近线都是水平的。
我们可以并且应该利用这一点来简化计算函数渐近线的过程。有两种主要的方法来处理这个话题:
1. 首先计算水平渐近线
这种方法在我的视频课程《函数行为研究》中有所展示。
函数存在水平渐近线的条件是:
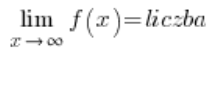 或者
或者 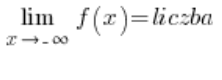
如果我们得到了水平渐近线,那么就不再计算斜渐近线了(因为就好像斜渐近线已经出现了一样 – 记住,水平的就是斜的)。但如果没有水平渐近线出现,那我们就有麻烦了 – 需要重新计算斜渐近线。
当然情况会更复杂一些:水平渐近线可能在 ![]() 出现,而在
出现,而在 ![]() 不出现。在这种情况下,我们不会在
不出现。在这种情况下,我们不会在 ![]() 研究斜渐近线的存在(因为它已经出现了),但我们需要在
研究斜渐近线的存在(因为它已经出现了),但我们需要在 ![]() 研究它的存在。
研究它的存在。
2. 首先计算斜渐近线
…然后水平渐近线可能会(或不会)自动出现,我们只需要正确解释答案。这种方法我没有在我的课程中展示。缺点是函数存在斜渐近线的条件稍微复杂一些:
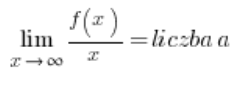 和
和 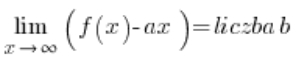
或:
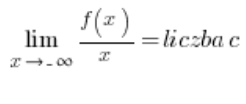 和
和 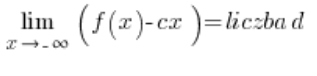
…而好处是,一旦计算完毕就不需要进一步计算了。如果条件得到满足,且根据斜渐近线存在的条件中的数值 ![]() (或
(或 ![]() )等于
)等于 ![]() ,这意味着斜渐近线实际上是水平渐近线。
,这意味着斜渐近线实际上是水平渐近线。
为了进一步简化工作,我们可以直接计算:
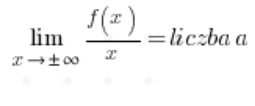 和
和 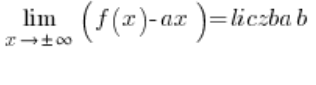
而只有在必要时(即当结果会因为 x 趋向于 ![]() 或
或 ![]() 而有所不同时),才分别计算
而有所不同时),才分别计算 ![]() 和
和 ![]() 的条件。
的条件。