No products in the cart.
Krystian Karczyński- 28 6 月 2024
- Komentarz 0
要回答标题中的问题，我们不需要回到斜渐近线的定义，只需要知道什么是函数。
像在数学中常见的情况一样，我们暂时假设函数图像在 
处有两条不同的斜渐近线，然后证明这个假设会导致矛盾，因此不能接受这个假设。
图像
在图像上，这些渐近线可能看起来像这样：
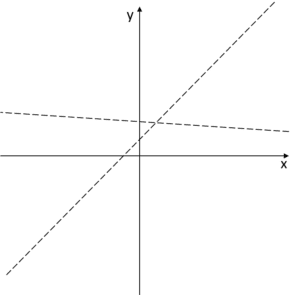而函数图像应在 处接近这些渐近线，因此它会看起来如下：
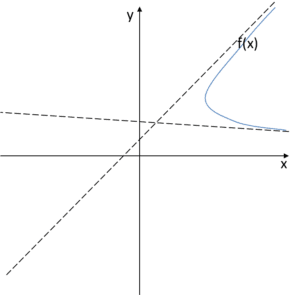怎么样？可以这样吗？函数图像可以这样吗？还是我们有问题？
问题
当然有问题。上述内容不能是函数图像。让我们回到定义，函数的定义是每个 x 对应仅一个 y 值。我们从图像中看到了什么？
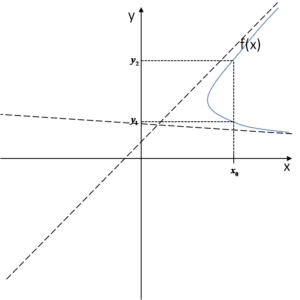我们看到参数 
对应两个值 – 
和 
。而函数图像中不能这样，因为每个 x 参数只能有一个 y 值。
因此，函数不能在 处有两条不同的斜渐近线。可以用同样的方法来证明对于 
🙂
