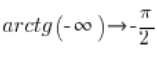Інверсні тригонометричні функції (Лекція)
Тема: Інверсні тригонометричні функції
Резюме
На цій лекції я введу поняття інверсних тригонометричних функцій: arcsinx, arccosx, arctgx, arcctgx. Це обернені функції до тригонометричних функцій.
Лекція складається з двох частин. У першій частині я показую, як швидко обчислити значення інверсних тригонометричних функцій, не вдаючись глибоко в тему (до цієї частини додається відео, фрагмент мого Курсу Інтегрального числення).
У другій частині я більш детально описую інверсні тригонометричні функції, показую їх графіки тощо.
Для розуміння лекції знадобляться:
- тригонометричні функції (середня школа)
Частина I
Інверсні тригонометричні функції – версія “ІНСТАНТ”
Інверсні тригонометричні функції простими словами – це обернені функції до тригонометричних функцій. Тобто arcsinx – це обернена функція до sinx.
Тобто, якщо ми знаємо, наприклад, що 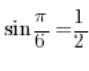 , це означає, що
, це означає, що ![]() .
.
І так далі:
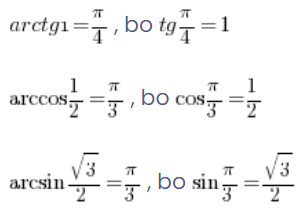
До того ж, у нас є кілька властивостей інверсних тригонометричних функцій, які дозволяють нам обчислювати їх значення навіть для негативних аргументів:
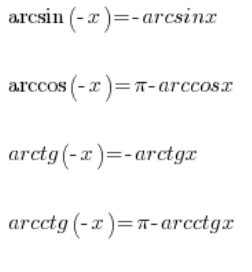
Тому ми можемо ще обчислити це:
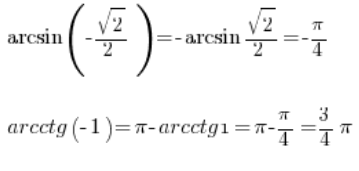
Отже, маючи таблицю тригонометричних функцій, ми можемо легко визначити значення інверсних тригонометричних функцій, просто читаючи її “навпаки”.
Я пояснюю це детальніше у відео тут:
Таблиця основних значень тригонометричних функцій з відео – завантажити тут.
Частина II
Інверсні тригонометричні функції – повна версія
Вступ – чому частина I недостатня
Виглядає на те, що у частині I ми визначили кожну інверсну тригонометричну функцію як обернену до відповідної тригонометричної функції.
Давайте формалізуємо це трохи. Ми сказали, що, наприклад, функція ![]() приймає значення
приймає значення ![]() , коли функція
, коли функція ![]() від цього
від цього ![]() дорівнює
дорівнює ![]() .
.
Відповідно:
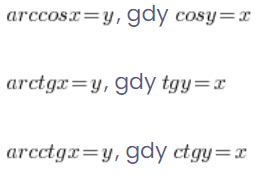
Тобто, якщо ми хочемо обчислити ![]() , ми задаємось питанням, косинус якого кута дає
, ми задаємось питанням, косинус якого кута дає ![]() , ми розуміємо, що це кут
, ми розуміємо, що це кут ![]() і отримуємо результат:
і отримуємо результат: 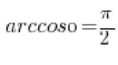 .
.
Чи це охоплює всі значення інверсних тригонометричних функцій?
Звичайно, НІ.
Давайте ще раз пройдемо весь процес міркування на конкретних числах (і, можливо, традиційно перейдемо до arcsinx):
Якщо ми хочемо обчислити  , ми задаємось питанням, синус якого кута дає
, ми задаємось питанням, синус якого кута дає ![]() , ми розуміємо, що це кут
, ми розуміємо, що це кут ![]() і отримуємо результат:
і отримуємо результат:  .
.
Де тут проблема? У виділеній частині:
Якщо ми хочемо обчислити  , ми задаємось питанням, синус якого кута дає
, ми задаємось питанням, синус якого кута дає ![]() , ми розуміємо, що це кут
, ми розуміємо, що це кут ![]() і отримуємо результат:
і отримуємо результат:  .
.
На жаль, не тільки синус ![]() дорівнює
дорівнює ![]() .
.
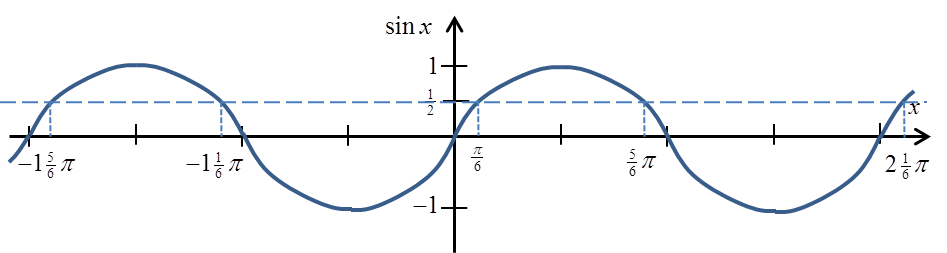
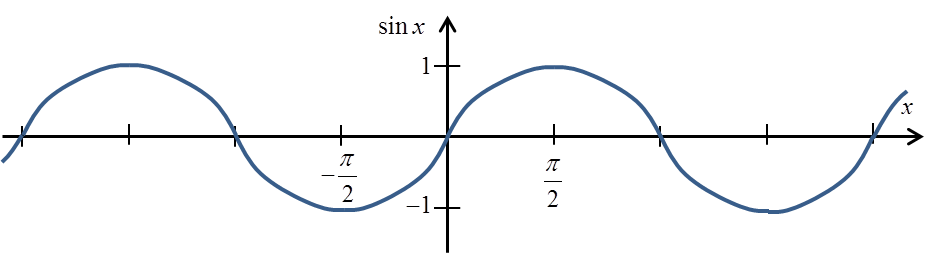
Згадаємо графік функції sinx (я на ньому відзначив значення ![]() ):
):
Ми бачимо і вже знаємо зі школи, що синус приймає значення ![]() не тільки для кута
не тільки для кута ![]() , але і для кутів:
, але і для кутів: 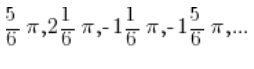
Тобто 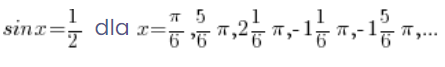
Згадаємо ще раз наш спосіб обчислення arcsin:
Якщо ми хочемо обчислити  , ми задаємось питанням, синус якого кута дає
, ми задаємось питанням, синус якого кута дає ![]() , ми розуміємо, що це кут
, ми розуміємо, що це кут ![]() і отримуємо результат:
і отримуємо результат:  .
.
Але тепер ми знаємо, що не тільки sin![]() дорівнює
дорівнює ![]() , тож виходить:
, тож виходить:
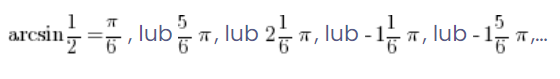
Це означало б, що arcsinx взагалі не є функцією, тому що одному аргументу відповідає кілька значень!
Надати чітку відповідь на питання, скільки дорівнює arcsin чогось, тоді було б зовсім неможливо.
Легко також уявити, що подібна проблема стосується будь-якої з тригонометричних функцій.
Професійніше кажучи: ці функції не є ін’єктивними, отже, їхні обернені функції не існують. У кожній тригонометричній функції кожне значення досягається для нескінченної кількості аргументів (вони є періодичними, правда?), тому при спробі визначити їхні обернені функції ми отримаємо нескінченну кількість значень для кожного аргументу. А в функціях так бути не може.
Що робити?
Це досить просто, не кажучи вже про примітивність. Кожну з тригонометричних функцій можна ОТРІЗАТИ так, щоб результатом була ін’єктивна функція.
Отже, визначимо правильно всі 4 циклометричні функції:
arcsinx
Пригадаймо графік функції sinx:
Якщо ми домовимося обрізати його, наприклад, до інтервалу ![]() , отримаємо такий графік:
, отримаємо такий графік:
![Wykres sinx w przedziale [0,pi] Obraz3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
На жаль, це не те, що нам потрібно, тому що це все ще не графік ін’єктивної функції, і проблема з значенням ![]() все ще існує:
все ще існує:
![Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2 Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
Тому ми домовляємося обрізати функцію sinx інакше, до аргументів 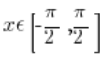 :
:
![Wykres funkcji sinx dla x należących do [-pi/2,pi/2] Wykres funkcji sinx dla x należących до [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
Тепер це ін’єктивна функція і має обернену функцію arcsinx.
Графік функції arcsinx виглядатиме приблизно так:

Її областю визначення є інтервал ![]() не існує.
не існує.
Точне визначення функції arcsinx таким чином:
![]() .
.
arccosx
Функція cosx також не є ін’єктивною:
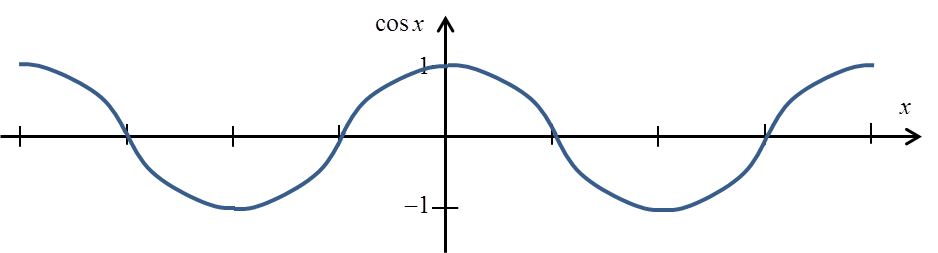
Щоб отримати ін’єктивну функцію, ми повинні обрізати її до інтервалу ![]() :
:
![Wykres funkcji cosx obciętej do przedziałу [0,pi] Wykres функції cosx obciętej до передзіалу [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
Таким чином, визначена функція вже є ін’єктивною і має обернену функцію arccosx.
Її графік буде приблизно таким:
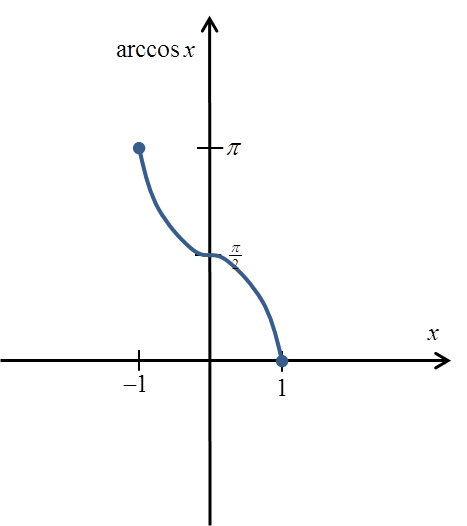
І її точне визначення:
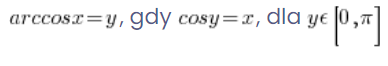 .
.
arctgx
Графік функції tgx виглядає так:

Це також не є ін’єктивною функцією! Ми можемо обрізати її наступним чином:
![Wykres funkcїї tgx obięty до передзіалу [-pi/2,pi/2] Wykres функції tgx obięty до передзіалу [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
Отримавши таким чином ін’єктивну функцію.
Графік функції arctgx виглядає так:

Її точне визначення таке:
![]() , для y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
, для y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
Ми також бачимо, що з графіку випливають деякі цікаві властивості, наприклад:
- область визначення функції arctgx – це весь набір дійсних чисел (ми можемо обчислити arctg з будь-якого числа)


arcctgx
З графіку функції ctgx:

Вирізаємо ін’єктивний шматок:
Графік функції arcctgx виглядає так:
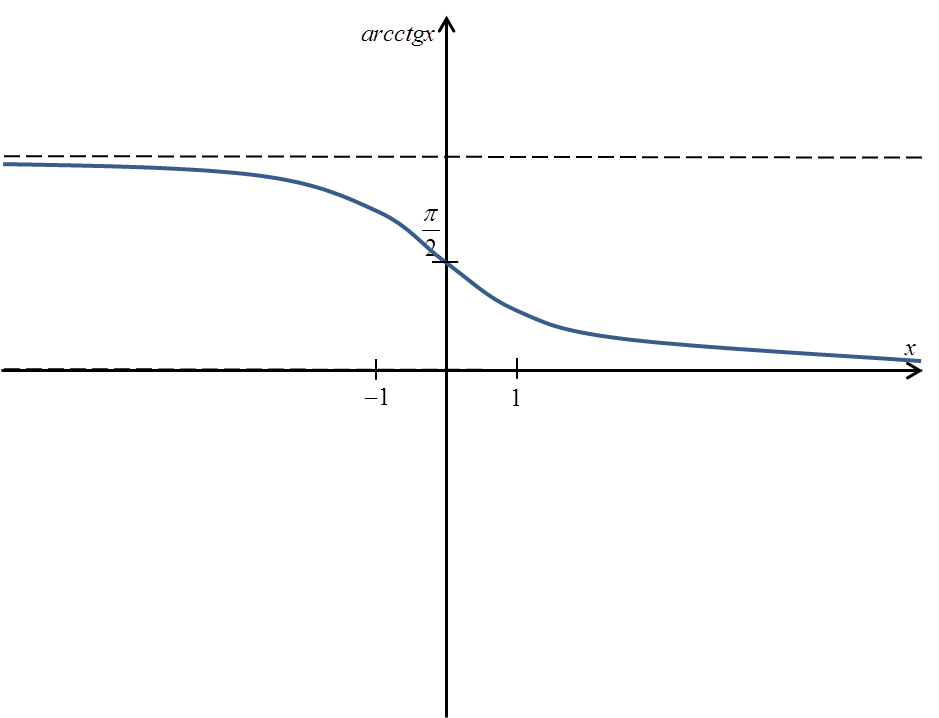
Точне визначення arcctgx було б таким:
![]() .
.
Ми бачимо, що:
- область визначення функції arcctgx – це весь набір дійсних чисел (ми можемо обчислити arcctg з будь-якого числа)


Примітка
У багатьох калькуляторах і загалом у математичних позначеннях (особливо західних) обернені тригонометричні функції позначаються не як “arcus”, а за допомогою показника -1. Наприклад, arcsinx записується як ![]() . Якщо ви знаєте, про що йдеться, то це не проблема. Однак можна зробити жахливу помилку і сплутати обернену функцію до sinx з функцією
. Якщо ви знаєте, про що йдеться, то це не проблема. Однак можна зробити жахливу помилку і сплутати обернену функцію до sinx з функцією ![]() , яка є зовсім іншою функцією, ніж arcsinx.
, яка є зовсім іншою функцією, ніж arcsinx.