Система рівнянь з параметром для визначення

Krystian Karczyński

Засновник та керівник сервісу eTrapez.

Магістр математики Познанської Політехніки (Польща). Репетитор з математики з багаторічним досвідом. Творець перших Курсів eTrapez, які здобули величезну популярність серед студентів у всій Польщі.

Живе у Щецині (Польща). Любить прогулянки лісом, відпочинок на пляжі та каякінг.

Обчисліть параметр ‘a’ у наведеній вище системі рівнянь, знаючи, що вона суперечлива.

Замість того, щоб систематично починати з обчислення рангу основної матриці, визначимо ранг доповненої матриці:

…він дорівнює двом, бо в цій матриці можна виділити ненульовий визначник другого порядку (більший вже не вийде):

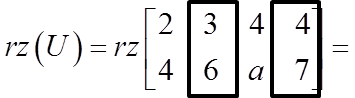
Тому ранг доповненої матриці дорівнює 2.

Застосування теореми Кронекера-Капеллі

Яким повинен бути ранг основної матриці?

Ми знаємо, що система суперечлива, і з теореми Кронекера-Капеллі ми знаємо, що вона буде суперечливою, коли ранг основної матриці відрізняється від рангу доповненої матриці. Ми також знаємо, що ранг основної матриці завжди менший або дорівнює рангу доповненої матриці (основна матриця міститься в доповненій). Отже, ранг основної матриці повинен бути 1 або 0 (щоб бути відмінним від рангу доповненої матриці).

Ранг основної матриці буде:

Ми бачимо, що він точно не буде дорівнювати 0 (лише ранг нульової матриці дорівнює 0) – отже, він повинен дорівнювати 1. Ранг буде один, коли перший і другий рядки будуть пропорційними (тоді ми викреслимо один із них). Ми бачимо, що перший рядок, помножений на два, дає другий рядок, якщо тільки a дорівнює 8.

Отже, швидко і без великих обчислень ми приходимо до відповіді: