Kalkulator do obliczania pochodnych online

Krystian Karczyński

Ogłoszenie

Niestety, po ponad 12 latach od udostępnienia przeze mnie darmowego kalkulatora pochodnych, musiałem go „wyłączyć”.

Kalkulator był prostym „widgetem” strony WolframAlpha. Jakiś czas temu Wolframalpha zmienił swoją politykę odnośnie widgetów. Między innymi: przestały one obliczać „na miejscu”, tylko przerzucają użytkownika na stronę WolframAlpha .

Przepraszam za kłopot wszystkich dotychczasowych użytkowników Kalkulatora Do Pochodnych. Przez długie lata bił on rekordy popularności jeśli chodzi o liczbę odwiedzających i zapytań.

Nowy kalkulator pochodnych

Zapraszam też do nowego kalkulatora pochodnych, stworzonego już przeze mnie w technologii Open Source. Dostęp do niego (i do innych interaktywnych narzędzi) uzyskać możecie w ramach subskrypcji za jedyne 5,99 zł / miesiąc na stronie:

Interaktywne Zadanie Domowe

A sam kalkulator wygląda tak:

Pozdrawiam i powodzenia!

Krystian Karczyński

konometria jest dosyć młodą dziedziną wypływającą z ekonomii i matematyki. W praktyce, dzięki modelom ekonometrycznym, możesz „zmierzyć gospodarkę”.Polega to konkretnie na zmierzeniu, jak zachowuje się jedna zmienna w zależności od innych. I na podstawie analizy tego, co było, możesz określać, co będzie się działo w przyszłości.

Wykorzystasz do tego przeróżne obliczenia, testy, schematy. Jedne będą bardzo proste, inne trudniejsze. Jednak najczęściej będzie się liczyło nie to, jak dojdziesz do wyniku, ale jak go zinterpretujesz, odczytasz i jakie wnioski wyciągniesz.

Poniższe Wykłady dotykają najważniejszych pojęć teoretycznych. Jestem przekonana, że pomogę Ci odkrywaniu tego, czym jest ekonometria. I przy okazji uda Ci się zaliczyć ten przedmiot na studiach.

310 Komentarzy

Karolina
25 listopada 2022 at 13:59

Mam problem z pochodą funkcji f(x)= arcsin(sqrt(x-1)) we wzorze na pochodną jest x^2 a w kalkulatorze wynik wychodzi bez kwadratu 🙁 nie wiem co robię źle.

Odpowiedz
1. Krystian Karczyński
  26 października 2023 at 15:41
  
  Rozwiązałem ten przykład krok po kroku, czy coś pomogłem?
:)
24 stycznia 2022 at 11:56

Dzień dobry mam problem z policzeniem tych pochodnych :Niech y = f(x) = cos 2x, g(x) = e^((1/3)*x)a) oblicz g'(3)b) oblicz (f(x)g(x))’c) oblicz (f(x)/g(x))’

Odpowiedz
1. Krystian Karczyński
  17 marca 2022 at 13:11
  
  a)
  
  $g'\left( x \right) = {\left( {{e^{{\textstyle{1 \over 3}}x}}} \right)^\prime } = {e^{{\textstyle{1 \over 3}}x}} \cdot {\left( {\frac{1}{3}x} \right)^\prime } = \frac{1}{3}{e^{{\textstyle{1 \over 3}}x}}$
  
  $g'\left( 3 \right) = \frac{1}{3}{e^{{{\frac{1}{3}}} \cdot 3}} = \frac{1}{3}e = \frac{e}{3}$
  
  b)
  
  $f\left( x \right)g\left( x \right) = \cos 2x \cdot {e^{{\textstyle{1 \over 3}}x}} = {e^{{\textstyle{1 \over 3}}x}}\cos 2x$
  
  ${\left[ {f\left( x \right)g\left( x \right)} \right]^\prime } = {\left( {{e^{{\textstyle{1 \over 3}}x}}\cos 2x} \right)^\prime } = {\left( {{e^{{\textstyle{1 \over 3}}x}}} \right)^\prime }\cos 2x + {e^{{\textstyle{1 \over 3}}x}}{\left( {\cos 2x} \right)^\prime } =$
  
  $= {e^{{\textstyle{1 \over 3}}x}}{\left( {\frac{1}{3}x} \right)^\prime }\cos 2x + {e^{{\textstyle{1 \over 3}}x}}\left( { – \sin 2x} \right) \cdot {\left( {2x} \right)^\prime } = \frac{1}{3}{e^{{\textstyle{1 \over 3}}x}}\cos 2x – 2{e^{{\textstyle{1 \over 3}}x}}\sin 2x =$
  
  $= {e^{{\textstyle{1 \over 3}}x}}\left( {\frac{1}{3}\cos 2x – 2\sin 2x} \right)$
politechnika lodzka
9 stycznia 2022 at 20:06

spoko opcja czasami korzystamy Pozdro

Odpowiedz
Klaudia
26 grudnia 2020 at 16:41

Dzień dobry, jak wprowadzic pierwiastek w kalkulator aby obejmował całe wyrażenie a nie tylko daną część?

Odpowiedz
Antytalencię
24 marca 2019 at 14:55

Dzień dobry.Nwm jak policzyć pochodną f(x) =sin(2 do x).Wię piszę tutaj

Odpowiedz
1. Krystian Karczyński
  27 października 2023 at 12:01
  
  Dzień dobry, pójdzie tak:
Krystian Karczyński
29 października 2018 at 19:17

Witam, polecam moją darmową Lekcję do liczenia pochodnej z definicji 🙂

A co przykładu, poleci tak:

Wzór na pochodną w punkcie $x subscript 0$ z definicji to:

$f apostrophe open parentheses x subscript 0 close parentheses equals limit as increment x rightwards arrow 0 of fraction numerator f open parentheses x subscript 0 plus increment x close parentheses minus f open parentheses x subscript 0 close parentheses over denominator increment x end fraction$

W naszym przypadku $f open parentheses x close parentheses equals fraction numerator 1 over denominator 5 x plus 6 end fraction$ .

Mamy więc:

$f apostrophe open parentheses x subscript 0 close parentheses equals limit as increment x rightwards arrow 0 of fraction numerator begin display style fraction numerator 1 over denominator 5 open parentheses x subscript 0 plus increment x close parentheses plus 6 end fraction end style minus begin display style fraction numerator 1 over denominator 5 x subscript 0 plus 6 end fraction end style over denominator increment x end fraction equals limit as increment x rightwards arrow 0 of fraction numerator begin display style fraction numerator 1 over denominator 5 x subscript 0 plus 5 increment x plus 6 end fraction minus fraction numerator 1 over denominator 5 x subscript 0 plus 6 end fraction end style over denominator increment x end fraction equals equals limit as increment x rightwards arrow 0 of fraction numerator begin display style fraction numerator 5 x subscript 0 plus 6 over denominator open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction minus fraction numerator 5 x subscript 0 plus 5 increment x plus 6 over denominator open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction end style over denominator increment x end fraction equals$

$equals limit as increment x rightwards arrow 0 of fraction numerator begin display style fraction numerator 5 x subscript 0 plus 6 minus open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses over denominator open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction end style over denominator increment x end fraction equals limit as increment x rightwards arrow 0 of fraction numerator begin display style fraction numerator 5 x subscript 0 plus 6 minus 5 x subscript 0 minus 5 increment x minus 6 over denominator open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction end style over denominator increment x end fraction equals equals limit as increment x rightwards arrow 0 of fraction numerator begin display style fraction numerator negative 5 increment x over denominator open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction end style over denominator increment x end fraction equals limit as increment x rightwards arrow 0 of fraction numerator negative 5 increment x over denominator open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction fraction numerator begin display style 1 end style over denominator increment x end fraction equals equals limit as increment x rightwards arrow 0 of fraction numerator negative 5 over denominator open parentheses 5 x subscript 0 plus 5 increment x plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction equals fraction numerator negative 5 over denominator open parentheses 5 x subscript 0 plus 6 close parentheses open parentheses 5 x subscript 0 plus 6 close parentheses end fraction equals fraction numerator negative 5 over denominator open parentheses 5 x subscript 0 plus 6 close parentheses squared end fraction$

Sprawdzamy prawdziwość tego wyniku korzystając ze wzorów:

$f apostrophe open parentheses x subscript 0 close parentheses equals open parentheses fraction numerator 1 over denominator 5 x subscript 0 plus 6 end fraction close parentheses apostrophe equals open square brackets open parentheses 5 x subscript 0 plus 6 close parentheses to the power of negative 1 end exponent close square brackets apostrophe equals negative 1 times open parentheses 5 x subscript 0 plus 6 close parentheses to the power of negative 1 minus 1 end exponent open parentheses 5 x subscript 0 plus 6 close parentheses apostrophe equals equals negative 1 open parentheses 5 x subscript 0 plus 6 close parentheses to the power of negative 2 end exponent times 5 equals fraction numerator negative 5 over denominator open parentheses 5 x subscript 0 plus 6 close parentheses squared end fraction$

Czyli wszystko gra 🙂

Odpowiedz
Magda
19 października 2018 at 20:22

Witam,

mam problem z rozwiązaniem takiego zadania:

Oblicz z definicji pochodną f(x)= 1/(5x+6) w punkcie x0. Poprawność sprawdź z wzorów na pochodne.

Z góry dziękuję za pomoc.

Odpowiedz
Natalia
9 kwietnia 2018 at 20:05

Panie Krystianie, nie do końca wiem jak obliczyć pochodną z funkcji (2x^6-16x^3)/(x^3-2)^2. Mógłby Pan mi prosze pomóc? 🙂

Odpowiedz
1. Joanna Grochowska
  16 maja 2018 at 11:59
  
  Pochodna z $fraction numerator 2 x to the power of 6 minus 16 x cubed over denominator open parentheses x cubed minus 2 close parentheses squared end fraction$ .
  
  Na początku mamy tutaj dzielenie dwóch funkcji, więc zaczynamy od zastosowania wzoru: $open parentheses f over g close parentheses apostrophe equals fraction numerator f apostrophe space times g space minus space f times g apostrophe over denominator g squared end fraction$
  
  $f equals 2 x to the power of 6 minus 16 x cubed$ – tutaj spoko, licząc pochodną wykorzystujemy liniowość, czyli pochodna z każdego składnika oddzielnie oraz dwa proste wzory: $open square brackets a times f \left parenthesis x \right parenthesis close square brackets apostrophe equals a times open square brackets f \left parenthesis x \right parenthesis close square brackets apostrophe$ (stała przed pochodną po x-sie), a także wzór: $open parentheses x to the power of n close parentheses apostrophe equals n times x to the power of n minus 1 end exponent$ .
  
  $g equals open parentheses x cubed minus 2 close parentheses squared$ – tutaj występuje takie coś jak złożenie funkcji. Masz jakieś wyrażenie podniesione do potęgi drugiej, czyli $open parentheses co ś close parentheses to the power of n$ . Przy liczeniu pochodnej wykorzystujesz wzór na $open parentheses x to the power of n close parentheses apostrophe equals n times x to the power of n minus 1 end exponent$ , z tym, że trzeba pamiętać do DOMNOŻENIU jeszcze pochodnej tego czegoś więcej, tego wyrażenia „coś”, czyli: $open parentheses open parentheses co ś close parentheses to the power of n space close parentheses apostrophe equals space n times open parentheses co ś close parentheses to the power of n minus 1 end exponent times open parentheses c o ś close parentheses apostrophe$
  
  No tu wyjdzie ostatecznie:
  
  $open square brackets fraction numerator 2 x to the power of 6 minus 16 x cubed over denominator open parentheses x cubed minus 2 close parentheses squared end fraction close square brackets apostrophe equals fraction numerator open parentheses 2 x to the power of 6 minus 16 x cubed close parentheses apostrophe times space open parentheses x cubed minus 2 close parentheses squared space minus space open parentheses 2 x to the power of 6 minus 16 x cubed close parentheses times space open square brackets open parentheses x cubed minus 2 close parentheses squared close square brackets apostrophe over denominator open square brackets open parentheses x cubed minus 2 close parentheses squared close square brackets squared end fraction equals$
  
  $equals fraction numerator open parentheses 2 times 6 times x to the power of 5 minus 16 times 3 times x squared close parentheses times space open parentheses x cubed minus 2 close parentheses squared space minus space open parentheses 2 x to the power of 6 minus 16 x cubed close parentheses times space open square brackets 2 times open parentheses x cubed minus 2 close parentheses to the power of 1 times open parentheses x cubed minus 2 close parentheses apostrophe close square brackets over denominator open parentheses x cubed minus 2 close parentheses to the power of 4 end fraction equals$
  
  $equals fraction numerator open parentheses 12 x to the power of 5 minus 48 x squared close parentheses times open parentheses x cubed minus 2 close parentheses squared space minus space open parentheses 2 x to the power of 6 minus 16 x cubed close parentheses times space open square brackets 2 open parentheses x cubed minus 2 close parentheses times open parentheses 3 times x squared minus 0 close parentheses close square brackets over denominator open parentheses x cubed minus 2 close parentheses to the power of 4 end fraction equals$
  
  $equals fraction numerator open parentheses 12 x to the power of 5 minus 48 x squared close parentheses times open parentheses x cubed minus 2 close parentheses squared space minus space open parentheses 2 x to the power of 6 minus 16 x cubed close parentheses times space 6 x squared open parentheses x cubed minus 2 close parentheses over denominator open parentheses x cubed minus 2 close parentheses to the power of 4 end fraction equals$
  
  $equals fraction numerator open parentheses x cubed minus 2 close parentheses open square brackets open parentheses 12 x to the power of 5 minus 48 x squared close parentheses times open parentheses x cubed minus 2 close parentheses space minus space open parentheses 2 x to the power of 6 minus 16 x cubed close parentheses times space 6 x squared close square brackets over denominator open parentheses x cubed minus 2 close parentheses to the power of 4 end fraction equals$
  
  $equals fraction numerator 12 x to the power of 8 minus 24 x to the power of 5 minus 48 x to the power of 5 plus 96 x squared minus space 12 x to the power of 8 plus 96 x to the power of 5 over denominator open parentheses x cubed minus 2 close parentheses cubed end fraction equals fraction numerator 24 x to the power of 5 plus 96 x squared over denominator open parentheses x cubed minus 2 close parentheses cubed end fraction equals fraction numerator bold 24 bold x to the power of bold 2 open parentheses bold x to the power of bold 3 bold plus bold 4 close parentheses over denominator open parentheses bold x to the power of bold 3 bold minus bold 2 close parentheses to the power of bold 3 end fraction$
damian
5 kwietnia 2018 at 19:51

x^2+e^x/x-lnx czy pomoze ktoś ?

Odpowiedz
1. Krystian Karczyński
  30 października 2023 at 12:03
  
  Jeżeli dobrze odczytałem zapis, to pójdzie tak:
Kamila
20 stycznia 2018 at 20:24

WitamMam problem z pochodna x^x jak to obliczyc?

Odpowiedz
1. Joanna Grochowska
  16 maja 2018 at 12:10
  
  Myślę, że ten filmik będzie baaardzo pomocny i wszystko wyjaśniający (chociaż przykład jest lekko inny) 🙂
  
  W Pani przypadku wyjdzie ostatecznie:
  
  $open parentheses x to the power of x close parentheses apostrophe space equals open parentheses e to the power of ln x to the power of x end exponent close parentheses apostrophe equals space open parentheses e to the power of x times ln x end exponent close parentheses apostrophe equals open parentheses e to the power of x times ln x end exponent close parentheses times open parentheses x times ln x close parentheses apostrophe space equals$
  
  $equals open parentheses e to the power of x times ln x end exponent close parentheses times open parentheses open parentheses x close parentheses apostrophe times ln x plus x times open parentheses ln x close parentheses apostrophe close parentheses equals space open parentheses e to the power of x times ln x end exponent close parentheses times open parentheses 1 times ln x plus x times 1 over x close parentheses equals$
  
  $equals bold space straight e to the power of straight x times lnx end exponent times open parentheses lnx plus 1 close parentheses space equals space straight e to the power of lnx to the power of x end exponent times open parentheses lnx plus 1 close parentheses space equals space bold italic x to the power of bold x bold times open parentheses bold l bold n bold x bold plus bold 1 close parentheses$
2. Krystian Karczyński
  31 października 2023 at 15:57
  
  Pójdzie tak:
Ania
21 grudnia 2017 at 18:22

Cześć!Mam problem z pochodną 6x(x^2+1)^2 mógłbys wytłumaczyc krok po kroku?

Odpowiedz
1. Krystian Karczyński
  31 października 2023 at 17:10
  
  Tak, zapraszam:
Ewusia
17 listopada 2017 at 17:58

Witam serdecznie. Mam problem z pochodną f(x)= 3/((1-x^2)(1-2x^3)). Kalkulator pokazuje odpowiedź: 6x(-5x^3+3x+1)/(mianownik^2). A w moich obliczeniach wszystko się zgadza oprócz tego, że mam -6x. Ktoś wie co się stało z tym minusem? Proszę o odpowiedź

Odpowiedz
1. Krystian Karczyński
  31 października 2023 at 17:26
  
  W pewnym momencie można wyciagnąć -2x przed nawias:
Anna
2 listopada 2017 at 11:14

Witam. Mam problem z policzeniem pochodnej f(x)=ln(x)log_2(x)

Odpowiedz
Agata
11 września 2017 at 11:42

Witam, nie rozumiem dlaczego pochodna z funkcji f(x)=e^2x+e^-x wychodzi e^2-e^-x a nie 2e^2x-e^-xBardzo proszę o odp

Odpowiedz
Robert
26 lipca 2017 at 15:23

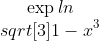
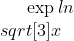
Witammam policzyć pochodne i nie potrafię sobie z nimi poradzić: 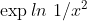$\exp ln\\sqrt[3]{1 - x^3}$ $\exp ln\\sqrt[3]{ x}$ $\exp {ln\1/x^2}$ mogę prosić o pomoc

Odpowiedz
Lidia
21 czerwca 2017 at 08:44

dzień dobry,czy ktoś może wie w jaki sposób krok po kroku obliczyć pochodną poniższej funkcji? $y equals fraction numerator x cubed sin open parentheses fourth root of 3 x end root close parentheses over denominator cos open parentheses x close parentheses end fraction$ Będę wdzięczna za pomoc 🙂

Odpowiedz
Kasiek
8 kwietnia 2017 at 12:45

Dzień dobry,zasanowiła mnie jedna rzecz. Chcąc sprawdzić wynik pochodnej (-8cos(x)sin(x))’ znalałzam Pana kalkulator i inny. wg Pana kalkulatora wynik to (-8cos(2x)), a to wyszło w innym (8(sinx)^2 – 8(cosx)^2) – i ja też otrzymałam taki wynik. Mogę prosić o pomoc?To całe zadanie jaki muszę obliczyć: -8cos(x)sin(x)+(e^(x^(1/2))(1- (1/x^(1/2))) /(4x))”Podzieliłam” je na 2 zgodnie z właściwościami pochodnych – [f(x)+g(x)]’ = f'(x)+g'(x)

Odpowiedz
1. Joanna Grochowska
  14 kwietnia 2017 at 10:32
  
  „wg Pana kalkulatora wynik to (-8cos(2x)), a to wyszło w innym (8(sinx)^2 – 8(cosx)^2) – i ja też otrzymałam taki wynik.”
  
  Pani Kasiu – oba wyniki są poprawne 🙂 Policzyła Pani wszystko prawidłowo.
  
  Kalkulator zamieszczony na Blogu po prostu dodatkowo dokonał jeszcze jedne przekształcenie, wykorzystując rozpisanie wzoru $cos \left parenthesis 2 x \right parenthesis$ ze szkoły średniej (jak pamiętamy, tam były jego 3 wersje)
  
  $cos \left parenthesis 2 x \right parenthesis equals cos squared x minus sin squared x space equals space 2 cos squared x minus 1 space equals space 1 minus 2 sin squared x$ – wykorzystana została wersja pierwsza.
  
  Rozpisując Pani wynik:
  
  $8 sin squared x space – space 8 cos squared x equals negative 8 times open parentheses negative sin squared x space plus cos squared x close parentheses equals negative 8 open parentheses bold italic c bold italic o bold italic s to the power of bold 2 bold italic x bold minus bold italic s bold italic i bold italic n to the power of bold 2 bold italic x close parentheses equals negative 8 bold italic c bold italic o bold italic s bold \left parenthesis bold 2 bold italic x bold \right parenthesis$
Bubi
14 lutego 2017 at 17:42

mam problem z pochodną funkcji : $left parenthesis 1 plus square root of x \right parenthesis to the power of ln square root of x end exponent$

Odpowiedz
kati
9 lutego 2017 at 21:36

$square root of 1 minus 3 x hat 2 end root equals$ … ; $2 to the power of 3 x plus 4 end exponent ln x equals$ … proszę o pomoc

Odpowiedz
1. kati
  9 lutego 2017 at 21:37
  
  oczywiście polecenie policz pochodne
2. Ryhor Abramovich
  17 lutego 2017 at 15:23
  
  1. $y equals square root of 1 minus 3 x squared end root$
  
  Stosuję wzór $open parentheses square root of triangle close parentheses apostrophe equals fraction numerator 1 over denominator 2 square root of triangle end fraction times triangle apostrophe$
  
  $y apostrophe equals fraction numerator 1 over denominator 2 square root of 1 minus 3 x squared end root end fraction times open parentheses 1 minus 3 x squared close parentheses apostrophe equals fraction numerator 1 over denominator 2 square root of 1 minus 3 x squared end root end fraction times open parentheses 0 minus 3 times 2 x close parentheses equals$
  
  $fraction numerator negative 6 x over denominator 2 square root of 1 minus 3 x squared end root end fraction equals negative fraction numerator 3 x over denominator square root of 1 minus 3 x squared end root end fraction$
  
  2. $y equals 2 to the power of 3 x plus 4 end exponent times ln x$
  
  Stosuję wzory: $open parentheses u times v close parentheses apostrophe equals u apostrophe times v plus u times v apostrophe$ oraz $open parentheses 2 to the power of triangle close parentheses apostrophe equals 2 to the power of triangle times ln 2 times triangle apostrophe$
  
  $y apostrophe equals open parentheses 2 to the power of 3 x plus 4 end exponent close parentheses apostrophe times ln x plus 2 to the power of 3 x plus 4 end exponent times open parentheses ln x close parentheses apostrophe equals 2 to the power of 3 x plus 4 end exponent times ln 2 times open parentheses 3 x plus 4 close parentheses apostrophe times ln x plus 2 to the power of 3 x plus 4 end exponent times 1 over x equals$
  
  $2 to the power of 3 x plus 4 end exponent times ln 2 times open parentheses 3 plus 0 close parentheses times ln x plus 2 to the power of 3 x plus 4 end exponent times 1 over x equals 2 to the power of 3 x plus 4 end exponent times open parentheses 3 ln 2 times ln x plus 1 over x close parentheses$
kati
9 lutego 2017 at 21:01

$space p r o s z ę space o space r a t u n e k space m a m space d o space p o l i c z e n i a space d w i e space p o c h o d n e space square root of 1 minus 3 x hat 2 end root space space$ $2 to the power of 3 x plus 4 end exponent ln x$

Odpowiedz
Kamil
9 lutego 2017 at 13:00

$3 ln hat 5 \left parenthesis 3 over x to the power of 4 minus x \right parenthesis$ Witam mam problem z obliczeniem tej pochodnej mógłby mi ktoś wytłumaczyć jak to zrobić ?

Odpowiedz
1. Ryhor Abramovich
  17 lutego 2017 at 15:13
  
  $y equals 3 ln to the power of 5 open parentheses 3 over x to the power of 4 minus x close parentheses$
  
  Stosuję wzory $open parentheses C times f open parentheses x close parentheses close parentheses apostrophe equals C times f apostrophe open parentheses x close parentheses$ oraz $open parentheses triangle to the power of 5 close parentheses apostrophe equals 5 times triangle to the power of 4 times triangle apostrophe$
  
  $y apostrophe equals 3 times open square brackets ln to the power of 5 open parentheses 3 over x to the power of 4 minus x close parentheses close square brackets apostrophe equals 3 times 5 times ln to the power of 4 open parentheses 3 over x to the power of 4 minus x close parentheses times open parentheses 3 over x to the power of 4 minus x close parentheses apostrophe equals$
  
  $15 ln to the power of 4 open parentheses 3 over x to the power of 4 minus x close parentheses times open parentheses 3 times x to the power of negative 4 end exponent minus x close parentheses apostrophe equals 15 ln to the power of 4 open parentheses 3 over x to the power of 4 minus x close parentheses times open parentheses 3 times open parentheses negative 4 close parentheses times x to the power of negative 5 end exponent minus 1 close parentheses equals$
  
  $15 ln to the power of 4 open parentheses 3 over x to the power of 4 minus x close parentheses times open parentheses negative 12 over x to the power of 5 minus 1 close parentheses equals negative 15 times open parentheses 12 over x to the power of 5 plus 1 close parentheses times ln to the power of 4 open parentheses 3 over x to the power of 4 minus x close parentheses$
Mati
7 lutego 2017 at 23:05

w kalkulatorze wychodzą bzdury gdy liczy się pochodną pierwiastków:np po wpisaniu (x^2)^-2 czyli $square root of cross times squared end root$ (pochodna to oczywiście 1) wychodzi

Odpowiedz
1. Joanna Grochowska
  8 lutego 2017 at 12:39
  
  Tutaj akurat kalkulator dobrze policzył pochodną 🙂
  
  Wpisana formuła „(x^2)^-2” (potęga (-2) ) nie oznacza pierwiastka, tylko inna potęgę, a mianowicie:
  $open parentheses x squared close parentheses to the power of negative 2 end exponent equals open parentheses 1 over x squared close parentheses squared equals 1 over x to the power of 4 equals x to the power of negative 4 end exponent$ – minus w potędze odwraca podstawę 🙂
  
  Aby wprowadzić pierwiastek, trzeba wziąć potęgę ułamkową, czyli powinien Pan wpisać „”(x^2)^(1/2)”
  
  Wtedy pochodna:
  
  $open parentheses square root of x squared end root close parentheses apostrophe equals open parentheses fraction numerator 1 over denominator 2 square root of x squared end root end fraction close parentheses times open parentheses x squared close parentheses apostrophe equals fraction numerator 2 x over denominator 2 square root of x squared end root end fraction equals fraction numerator x over denominator square root of x squared end root end fraction equals fraction numerator x over denominator open vertical bar x close vertical bar end fraction equals open curly brackets table attributes columnalign \left end attributes row cell 1 space space space space space space d l a space x greater or equal than 0 end cell row cell negative 1 space space space d l a space x less than 0 end cell end table close$
Paulina
29 stycznia 2017 at 13:54

Witam Panie Krzysztofie,czy mógłby mi Pan pomóc z obliczeniem pochodnej: $f \left parenthesis x \right parenthesis equals fifth root of fraction numerator cos squared x over denominator x cubed minus 3 x end fraction end root$

Odpowiedz
1. Ryhor Abramovich
  17 lutego 2017 at 21:36
  
  $y equals fifth root of fraction numerator cos squared x over denominator x cubed minus 3 x end fraction end root$
  
  Stosuję wzory dla pochodnej ułamku:
  
  $open parentheses u over v close parentheses apostrophe equals fraction numerator u apostrophe times v minus u times v apostrophe over denominator v squared end fraction$ oraz pochodnej funkcji złożonej:
  
  $open square brackets f open parentheses g open parentheses x close parentheses close parentheses close square brackets apostrophe equals f apostrophe open parentheses g close parentheses times g apostrophe open parentheses x close parentheses$
  
  $y equals fifth root of fraction numerator cos squared x over denominator x cubed minus 3 x end fraction end root equals open parentheses fraction numerator cos squared x over denominator x cubed minus 3 x end fraction close parentheses to the power of 1 fifth end exponent$ . Wtedy
  
  $y apostrophe equals 1 fifth times open parentheses fraction numerator cos squared x over denominator x cubed minus 3 x end fraction close parentheses to the power of 1 fifth minus 1 end exponent times open parentheses fraction numerator cos squared x over denominator x cubed minus 3 x end fraction close parentheses apostrophe equals 1 fifth times open parentheses fraction numerator cos squared x over denominator x cubed minus 3 x end fraction close parentheses to the power of negative 4 over 5 end exponent times$
  
  $times fraction numerator open parentheses cos squared x close parentheses apostrophe times open parentheses x cubed minus 3 x close parentheses minus cos squared x times open parentheses x cubed minus 3 x close parentheses apostrophe over denominator open parentheses x cubed minus 3 x close parentheses squared end fraction equals 1 fifth times fraction numerator 1 over denominator fifth root of open parentheses \begin display style fraction numerator cos squared x over denominator x cubed minus 3 x end fraction end style close parentheses to the power of 4 end root end fraction times$
  
  $times fraction numerator 2 cos x times open parentheses cos x close parentheses apostrophe times open parentheses x cubed minus 3 x close parentheses minus cos squared x times open parentheses 3 x squared minus 3 close parentheses over denominator open parentheses x cubed minus 3 x close parentheses squared end fraction equals$
  
  $1 fifth times fifth root of open parentheses fraction numerator x cubed minus 3 x over denominator cos squared x end fraction close parentheses to the power of 4 end root times fraction numerator 2 cos x times open parentheses negative sin x close parentheses times open parentheses x cubed minus 3 x close parentheses minus cos squared x times open parentheses 3 x squared minus 3 close parentheses over denominator open parentheses x cubed minus 3 x close parentheses squared end fraction equals$
  
  $1 fifth times fraction numerator fifth root of open parentheses x cubed minus 3 x close parentheses to the power of 4 end root over denominator fifth root of open parentheses cos squared x close parentheses to the power of 4 end root end fraction times fraction numerator negative cos x times open square brackets 2 sin x times open parentheses x cubed minus 3 x close parentheses plus cos x times open parentheses 3 x squared minus 3 close parentheses close square brackets over denominator fifth root of open parentheses open parentheses x cubed minus 3 x close parentheses squared close parentheses to the power of 5 end root end fraction equals$
  
  $equals negative 1 fifth times fraction numerator fifth root of open parentheses x cubed minus 3 x close parentheses to the power of 4 end root over denominator fifth root of cos to the power of 8 x end root end fraction times fraction numerator fifth root of cos to the power of 5 x end root times open square brackets 2 times open parentheses x cubed minus 3 x close parentheses times sin x plus open parentheses 3 x squared minus 3 close parentheses times cos x close square brackets over denominator fifth root of open parentheses x cubed minus 3 x close parentheses to the power of 10 end root end fraction equals$
  
  $equals negative 1 fifth times fraction numerator 2 times open parentheses x cubed minus 3 x close parentheses times sin x plus open parentheses 3 x squared minus 3 close parentheses times cos x over denominator fifth root of open parentheses x cubed minus 3 x close parentheses to the power of 6 times cos cubed x end root end fraction$
Mike
22 stycznia 2017 at 17:14

Dzień dobry, chciałem zwrócić uwagę na błąd, gdy w pochodnej funkcji sqrt(3^3 -2) wynikiem jest ((3^x)log(3))/(2(sqrt(3x-2))), gdzie w miejscu log powinno być ln.Pozdrawiam

Odpowiedz
Justyna
11 stycznia 2017 at 16:57

Witam, w ostatniej lekcji z kursu pochodnych robił Pan przykład x/lnx, Moje pytanie brzmi skąd w wykresie 2 pochodnej wziął się punkt 1. wklejam juz policzoną 2 pochodną

Odpowiedz
Mateusz
31 grudnia 2016 at 11:31

Dzień dobry Panie Krystianie!Czy mógłby mi Pan pomóc w obliczeniu pochodnej z: $left parenthesis sin x plus cos x \right parenthesis to the power of 5$ * $fifth root of vertical line a r c sin x plus a r c cos x vertical line end root$ ?

Odpowiedz
1. Ryhor Abramovich
  19 stycznia 2017 at 02:33
  
  $y equals open parentheses sin x plus cos x close parentheses to the power of 5 times fifth root of open vertical bar a r s c i n x plus a r c cos x close vertical bar end root$
  
  Wiadomo, że pochodna liczby stałej wynosi zero:
  
  $C apostrophe equals 0$ , o ile $C equals c o n s t space open parentheses s t a ł a close parentheses$
  
  Obliczymy:
  
  $open parentheses a r c sin x plus a r c cos x close parentheses apostrophe equals open parentheses a r c sin x close parentheses apostrophe plus open parentheses a r c cos x close parentheses apostrophe equals fraction numerator 1 over denominator square root of 1 minus x squared end root end fraction plus open parentheses negative fraction numerator 1 over denominator square root of 1 minus x squared end root end fraction close parentheses equals 0$
  
  Stąd mamy, że $a r c sin x plus a r c cos x equals C$
  
  Liczba stała nie zależy od x. Obliczymy ją:
  
  $a r c sin x plus a r c cos x equals C equals a r c sin 0 plus a r c cos 0 equals 0 plus \pi over 2 equals \pi over 2$
  
  Wtedy funkcja
  
  $y equals open parentheses sin x plus cos x close parentheses to the power of 5 times fifth root of open vertical bar a r c sin x plus a r c cos x close vertical bar end root equals fifth root of \pi over 2 end root times open parentheses sin x plus cos x close parentheses to the power of 5$ ,
  
  i jej pochodna
  
  (wg wzoru dla funkcji złożonej: $open parentheses triangle to the power of 5 close parentheses apostrophe equals 5 triangle to the power of 4 times open parentheses triangle close parentheses apostrophe$ )
  
  wynosi:
  
  $y apostrophe equals fifth root of \pi over 2 end root times 5 times open parentheses sin x plus cos x close parentheses to the power of 4 times open parentheses sin x plus cos x close parentheses apostrophe equals$
  
  $fifth root of \pi over 2 end root times open parentheses sin x plus cos x close parentheses to the power of 4 times open parentheses cos x minus sin x close parentheses$
Kasia
21 grudnia 2016 at 23:18

Witam, potrzebuję obliczyć pierwszą pochodną funkcji. Jak to zrobić?i(x) = 3e^2x *lnx

Odpowiedz
1. Ryhor Abramovich
  17 lutego 2017 at 21:44
  
  $y equals 3 e to the power of 2 x end exponent times ln x$
  
  Stosuję wzory: $open parentheses C times y close parentheses apostrophe equals C times y apostrophe$ (gdzie C – stała) oraz $open parentheses u times v close parentheses apostrophe equals u apostrophe times v plus u times v apostrophe$ , a także
  
  $open parentheses e to the power of triangle close parentheses apostrophe equals e to the power of triangle times triangle apostrophe$
  
  $y apostrophe equals 3 times open square brackets open parentheses e to the power of 2 x end exponent close parentheses apostrophe times ln x plus e to the power of 2 x end exponent times open parentheses ln x close parentheses apostrophe close square brackets equals 3 times open square brackets e to the power of 2 x end exponent times open parentheses 2 x close parentheses apostrophe times ln x plus e to the power of 2 x end exponent times 1 over x close square brackets equals$
  
  $3 times open parentheses e to the power of 2 x end exponent times 2 times ln x plus e to the power of 2 x end exponent times 1 over x close parentheses equals 3 times e to the power of 2 x end exponent times open parentheses 2 ln x plus 1 over x close parentheses$
Leszek
17 grudnia 2016 at 21:44

Witam,nie wiem czy kalkulator dobrze liczy ale wychodzi że (ln(x))’ = 1/x i to jest dobrze ale wpisując ln(2x) podaje wynik też 1/x czy to jest aby dobrze? Czy nie powinno być 2/x ?Proszę o szybką odpowiedź.

Odpowiedz
1. Joanna Grochowska
  7 lutego 2017 at 17:18
  
  Tutaj wynik jest poprawny, pochodna $open parentheses ln \left parenthesis 2 x \right parenthesis close parentheses apostrophe equals 1 over x$
  Bierze się to z tego, że jest to złożenie dwóch funkcji – nie ma Pan samego „x” w logarytmie tylko coś więcej. Przy liczeniu takich pochodnych, najpierw robimy pochodną tej funkcji „zewnętrznej” i domnażamy do niej pochodną funkcji w środku, tej „wewnętrznej”.
  
  Ogólnie na wzorach to idzie tak: $left parenthesis f \left parenthesis g \left parenthesis x \right parenthesis \right parenthesis apostrophe space equals space f apostrophe \left parenthesis g \left parenthesis x \right parenthesis \right parenthesis space times space g apostrophe \left parenthesis x \right parenthesis$
  
  Przy naszych danych to pójdzie tak: $open parentheses ln \left parenthesis increment \right parenthesis close parentheses apostrophe equals 1 over increment times increment apostrophe$ , gdzie za ten $increment$ biorę funkcję wewnętrzną.
  
  Stąd ostatecznie: $open parentheses ln \left parenthesis 2 x \right parenthesis close parentheses apostrophe equals fraction numerator 1 over denominator 2 x end fraction times open parentheses 2 x close parentheses apostrophe equals fraction numerator 1 over denominator 2 x end fraction times 2 times 1 equals fraction numerator 2 over denominator 2 x end fraction equals 1 over x$
Michał
14 grudnia 2016 at 23:58

Witam mógłby mi ktoś pomóc obliczyć pochodną funkcji y= $cube root of x to the power of 5 end root ln x$

Odpowiedz
1. Ryhor Abramovich
  17 lutego 2017 at 21:52
  
  $y equals cube root of x to the power of 5 end root times ln x equals x to the power of 5 over 3 end exponent times ln x$
  
  Stosuję wzór: $open parentheses u times v close parentheses apostrophe equals u apostrophe times v plus u times v apostrophe$
  
  $y apostrophe equals open parentheses x to the power of 5 over 3 end exponent close parentheses apostrophe times ln x plus x to the power of 5 over 3 end exponent times open parentheses ln x close parentheses apostrophe equals 5 over 3 times x to the power of 5 over 3 minus 1 end exponent times ln x plus x to the power of 5 over 3 end exponent times 1 over x equals$
  
  $5 over 3 times x to the power of 2 over 3 end exponent times ln x plus x to the power of \begin display style 5 over 3 end style end exponent over x equals 5 over 3 times x to the power of 2 over 3 end exponent times ln x plus x to the power of 5 over 3 minus 1 end exponent equals 5 over 3 times x to the power of 2 over 3 end exponent times ln x plus x to the power of 2 over 3 end exponent equals$
  
  $x to the power of 2 over 3 end exponent times open parentheses 5 over 3 ln x plus 1 close parentheses equals cube root of x squared end root times open parentheses 5 over 3 ln x plus 1 close parentheses$
marco
10 grudnia 2016 at 21:43

jak obliczyć pochodna funkcjiy= 4x^1/3 * (5 + 2*4^3^x)/x^2 + 1

Odpowiedz
1. Ryhor Abramovich
  19 stycznia 2017 at 02:15
  
  $y equals fraction numerator 4 cube root of x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses over denominator x squared plus 1 end fraction equals 4 times fraction numerator cube root of x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses over denominator x squared plus 1 end fraction$
  
  Stosuję wzory:
  
  $open parentheses u over v close parentheses apostrophe equals fraction numerator u apostrophe v minus u v apostrophe over denominator v squared end fraction$ oraz (pochodna funkcji złożonej) $open parentheses 4 to the power of triangle close parentheses apostrophe equals 4 to the power of triangle times ln 4 times open parentheses triangle close parentheses apostrophe$ , a także
  
  $open parentheses u times v close parentheses apostrophe equals u apostrophe v plus u v apostrophe$
  
  $y apostrophe equals 4 times fraction numerator open square brackets cube root of x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses close square brackets apostrophe times open parentheses x squared plus 1 close parentheses minus cube root of x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses times open parentheses x squared plus 1 close parentheses apostrophe over denominator open parentheses x squared plus 1 close parentheses squared end fraction equals$
  
  $4 times fraction numerator open square brackets open parentheses cube root of x close parentheses apostrophe times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses plus cube root of x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses apostrophe close square brackets times open parentheses x squared plus 1 close parentheses minus cube root of x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses times open parentheses 2 x plus 0 close parentheses over denominator open parentheses x squared plus 1 close parentheses squared end fraction equals$
  
  $4 times fraction numerator open square brackets open parentheses x to the power of \begin display style 1 third end style end exponent close parentheses apostrophe times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses plus cube root of x times open parentheses 0 plus 2 times 4 to the power of 3 to the power of x end exponent times ln 4 times open parentheses 3 to the power of x close parentheses apostrophe close parentheses close square brackets times open parentheses x squared plus 1 close parentheses minus cube root of x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses times 2 x over denominator open parentheses x squared plus 1 close parentheses squared end fraction equals$
  
  $4 times fraction numerator open square brackets \begin display style 1 third end style x to the power of negative \begin display style 2 over 3 end style end exponent times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses plus x to the power of \begin display style 1 third end style end exponent times 2 times 4 to the power of 3 to the power of x end exponent times ln 4 times 3 to the power of x times ln 3 close square brackets times open parentheses x squared plus 1 close parentheses minus x to the power of \begin display style 1 third end style end exponent times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses times 2 x over denominator open parentheses x squared plus 1 close parentheses squared end fraction equals$
  
  $4 times fraction numerator \begin display style 1 third end style x to the power of negative \begin display style 2 over 3 end style end exponent times open square brackets 5 plus 2 times 4 to the power of 3 to the power of x end exponent plus 3 x times 2 times 4 to the power of 3 to the power of x end exponent times 3 to the power of x times ln 4 times ln 3 close square brackets times open parentheses x squared plus 1 close parentheses minus \begin display style 1 third end style x to the power of negative \begin display style 2 over 3 end style end exponent times 3 x times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses times 2 x over denominator open parentheses x squared plus 1 close parentheses squared end fraction equals$
  
  $4 times 1 third x to the power of negative 2 over 3 end exponent times fraction numerator open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent plus 6 x times 4 to the power of 3 to the power of x end exponent times 3 to the power of x times ln 4 times ln 3 close parentheses times open parentheses x squared plus 1 close parentheses minus 6 x squared times open parentheses 5 plus 2 times 4 to the power of 3 to the power of x end exponent close parentheses over denominator open parentheses x squared plus 1 close parentheses squared end fraction equals$
  
  $4 over 3 x to the power of negative 2 over 3 end exponent times fraction numerator 5 x squared plus 5 plus 2 x squared times 4 to the power of 3 to the power of x end exponent plus 2 times 4 to the power of 3 to the power of x end exponent plus 6 x cubed times 4 to the power of 3 to the power of x end exponent times 3 to the power of x times ln 4 times ln 3 plus 6 x times 4 to the power of 3 to the power of x end exponent times 3 to the power of x times ln 4 times ln 3 minus 30 x squared minus 12 x squared times 4 to the power of 3 to the power of x end exponent over denominator open parentheses x squared plus 1 close parentheses squared end fraction equals$
  
  $4 over 3 times fraction numerator negative 25 x squared plus 5 minus 10 x squared times 4 to the power of 3 to the power of x end exponent plus 2 times 4 to the power of 3 to the power of x end exponent plus 6 x cubed times 4 to the power of 3 to the power of x end exponent times 3 to the power of x times ln 4 times ln 3 plus 6 x times 4 to the power of 3 to the power of x end exponent times ln 4 times ln 3 over denominator x to the power of \begin display style 2 over 3 end style end exponent times open parentheses x squared plus 1 close parentheses squared end fraction$
Klaudia
2 grudnia 2016 at 22:30

Witam, jak obliczyć pochodną funkcji f(x)= e^(2x+1)/(x-2)

Odpowiedz
Sylwia
18 listopada 2016 at 18:51

Witam, czy mógłby mi Pan wytłumaczyć jak rozwiązać taką pochodną:f(x)=xsinxlnx ?z góry dziękuje i pozdrawiam 🙂

Odpowiedz
1. Ryhor Abramovich
  19 stycznia 2017 at 01:29
  
  $f open parentheses x close parentheses equals x times sin x times ln x$
  
  Znany jest wzór dla pochodnej iloczynu:
  
  $open parentheses u times v close parentheses apostrophe equals u apostrophe v plus u v apostrophe$
  
  Spróbujemy otrzymać wzór dla iloczynu trzech czynników:
  
  $open parentheses u times v times w close parentheses apostrophe equals open square brackets u times open parentheses v times w close parentheses close square brackets apostrophe equals u apostrophe times open parentheses v times w close parentheses plus u times open parentheses v times w close parentheses apostrophe equals u apostrophe times v times w plus u times open parentheses v apostrophe times w plus v times w apostrophe close parentheses equals$
  
  $u apostrophe times v times w plus u times v apostrophe times w plus u times v times w apostrophe$
  
  Wtedy:
  
  $f apostrophe open parentheses x close parentheses equals open parentheses x times sin x times ln x close parentheses apostrophe equals x apostrophe times sin x times ln x plus x times open parentheses sin x close parentheses apostrophe times ln x plus x times sin x times open parentheses ln x close parentheses apostrophe equals$
  
  $1 times sin x times ln x plus x times cos x times ln x plus x times sin x times 1 over x equals sin x times ln x plus x times cos x times ln x plus sin x$
radek
14 listopada 2016 at 23:10

(2x-1)^4=8(2x-1)^3 dlaczego tak????

Odpowiedz
Jack
13 listopada 2016 at 19:53

Jak to obliczyć ? f(x)= $open parentheses fraction numerator 1 over denominator 2 square root of x end fraction minus 1 close parentheses x squared$

Odpowiedz
1. Anna Zalewska
  16 listopada 2016 at 22:38
Iza
13 listopada 2016 at 13:21

f(x)=x^2*(x-2)^2Wytłumaczysz mi jak to policzyłeś, trochę inaczej mam rozpisane z zajęć i się pogubiłam…? Z góry dziękuję 🙂

Odpowiedz
1. Ryhor Abramovich
  19 stycznia 2017 at 01:20
  
  $f open parentheses x close parentheses equals x squared times open parentheses x minus 2 close parentheses squared$
  
  Stosuję wzór:
  
  $open parentheses u times v close parentheses apostrophe equals u apostrophe v plus u v apostrophe$ oraz (pochodna funkcji złożonej) $open parentheses triangle squared close parentheses apostrophe equals 2 triangle times open parentheses triangle close parentheses apostrophe$
  
  $f apostrophe open parentheses x close parentheses equals open square brackets x squared times open parentheses x minus 2 close parentheses squared close square brackets apostrophe equals open parentheses x squared close parentheses apostrophe times open parentheses x minus 2 close parentheses squared plus x squared times open square brackets open parentheses x minus 2 close parentheses squared close square brackets apostrophe equals 2 x times open parentheses x minus 2 close parentheses squared plus$
  
  $plus x squared times 2 times open parentheses x minus 2 close parentheses times open parentheses x minus 2 close parentheses apostrophe equals 2 x times open parentheses x squared minus 4 x plus 4 close parentheses plus 2 x squared times open parentheses x minus 2 close parentheses times open parentheses 1 minus 0 close parentheses equals$
  
  $2 x cubed minus 8 x squared plus 8 x plus 2 x cubed minus 4 x squared equals 4 x cubed minus 12 x squared plus 8 x$
  
  Można było inaczej:
  
  $f open parentheses x close parentheses equals x squared times open parentheses x minus 2 close parentheses squared equals open square brackets x times open parentheses x minus 2 close parentheses close square brackets squared equals open parentheses x squared minus 2 x close parentheses squared equals x to the power of 4 minus 4 x cubed plus 4 x squared$
  
  Wtedy:
  
  $f apostrophe open parentheses x close parentheses equals open parentheses x to the power of 4 minus 4 x cubed plus 4 x squared close parentheses apostrophe equals 4 x cubed minus 4 times 3 x squared plus 4 times 2 x equals 4 x cubed minus 12 x squared plus 8 x$
michalaczek
30 października 2016 at 23:08

f(x)=ln $fifth root of e$

Odpowiedz
1. michalaczek
  30 października 2016 at 23:10
  
  czy moge zapisac w postaci $log subscript e e to the power of 5 equals 5$ ???
michalaczek
30 października 2016 at 23:06

1) f(x)= $e to the power of negative x end exponent$ 2) f(x)= $ln to the power of 8 x$ 3) f(x)=ln( $5 x to the power of 4 minus x plus 9$ )

Odpowiedz
michalaczek
30 października 2016 at 22:59

odp do f(x)= $square root of 4 x to the power of 7 plus 1 end root$ to $fraction numerator 14 x cubed over denominator square root of 4 x to the power of 7 plus 1 end root end fraction$ ???

Odpowiedz
1. Ryhor Abramovich
  19 stycznia 2017 at 01:04
  
  $f open parentheses x close parentheses equals square root of 4 x to the power of 7 plus 1 end root$
  
  Stosuję wzór na pochodne funkcji złożonej:
  
  $open parentheses square root of triangle close parentheses apostrophe equals fraction numerator 1 over denominator 2 square root of triangle end fraction times open parentheses triangle close parentheses apostrophe$
  
  $f apostrophe open parentheses x close parentheses equals fraction numerator 1 over denominator 2 square root of 4 x to the power of 7 plus 1 end root end fraction times open parentheses 4 x to the power of 7 plus 1 close parentheses apostrophe equals fraction numerator 4 times 7 x to the power of 6 plus 0 over denominator 2 square root of 4 x to the power of 7 plus 1 end root end fraction equals fraction numerator 28 x to the power of 6 over denominator 2 square root of 4 x to the power of 7 plus 1 end root end fraction equals fraction numerator 14 x to the power of 6 over denominator square root of 4 x to the power of 7 plus 1 end root end fraction$
michalaczek
30 października 2016 at 22:55

f(x)= $e to the power of 8 x end exponent$ ???

Odpowiedz
1. Joanna Grochowska
  14 lutego 2017 at 11:23
  
  Tutaj jest do policzenia pochodna funkcji złożonej, czyli argumentem nie jest sam „x” tylko coś więcej, nie ma po prostu $e to the power of x$ tylko $e to the power of c o ś end exponent$ .
  Postępujemy jak zawsze w takich przypadkach, czyli: pochodna tego co „na zewnątrz” pomnożyć razy pochodna funkcji wewnętrznej (coś więcej niż sam „x”), czyli jakby $open parentheses e to the power of increment close parentheses apostrophe equals e to the power of increment times increment apostrophe$ .
  
  Stąd: $open parentheses e to the power of 8 x end exponent close parentheses apostrophe equals e to the power of 8 x end exponent times open parentheses 8 x close parentheses apostrophe equals e to the power of 8 x end exponent times 8 times 1 equals 8 e to the power of 8 x end exponent$
michalaczek
30 października 2016 at 22:43

$square root of blank end root$ da wpisać się do kalkulatora?

Odpowiedz
1. Joanna Grochowska
  31 października 2016 at 20:04
  
  Tak, „pierwiastek” można wpisać na dwa sposoby
  
  1) wpisując: \sqrt(…) , np \sqrt(2x) oznacza $square root of 2 x end root$
  
  2) wpisując potęgę ułamkową , tzn. (…)^(1/2) , np (x)^(1/2) oznacza $square root of x$
michalaczek
30 października 2016 at 22:41

jak rozwiazac:1) f(x)= $bevelled fraction numerator a r c space cos space x over denominator x end fraction$ 2) f(x)= $bevelled fraction numerator a r c space sin space x over denominator x end fraction$ z góry bardzo dziękuje!

Odpowiedz
1. Ryhor Abramovich
  19 stycznia 2017 at 00:59
  
  1. $f open parentheses x close parentheses equals fraction numerator a r c cos x over denominator x end fraction$
  
  Skorzystam ze wzoru:
  
  $open parentheses u over v close parentheses apostrophe equals fraction numerator u apostrophe v minus u v apostrophe over denominator v squared end fraction$
  
  $f apostrophe open parentheses x close parentheses equals open parentheses fraction numerator a r c cos x over denominator x end fraction close parentheses apostrophe equals fraction numerator open parentheses a r c cos x close parentheses apostrophe times x minus a r c cos x times open parentheses x close parentheses apostrophe over denominator x squared end fraction equals$
  
  $fraction numerator negative \begin display style fraction numerator 1 over denominator square root of 1 minus x squared end root end fraction end style times x minus a r c cos x times 1 over denominator x squared end fraction equals negative fraction numerator \begin display style fraction numerator x over denominator square root of 1 minus x squared end root end fraction end style plus a r c cos x over denominator x squared end fraction equals$
  
  $negative fraction numerator x plus square root of 1 minus x squared end root times a r c cos x over denominator x squared times square root of 1 minus x squared end root end fraction$
Karolina
14 września 2016 at 00:46

czy mógłby ktoś mi pomóc z rozwiązaniem pochodnej: (x^2)/(2-x) ?
Kalkulator wylicza to jako: [-(x-4)x]/[(x-2)^2]
Ja wyliczam już czwarty raz i za każdym wychodzi mi taki sam wynik [(4-x)x]/[(2-x)^2], niestety inny niż kalkulatora 🙁
proszę o pomoc!

Odpowiedz
1. Joanna Grochowska
  14 września 2016 at 10:45
  
  Oba wyniki są poprawne i oba są identyczne 🙂
  
  Po prostu ten z kalkulatora wyliczony „wyciągnął” jeszcze minusy z każdego z wyrażeń.
  
  Przekształcę więc je tak, że na górze wciągnę go z powrotem, a na dole jakby go wyciągnę jeszcze raz (bo podniesiony do kwadratu się zredukował). Proszę popatrzeć:
  
  $\displaystyle \frac{{-(x-4)x}}{{{{{(x-2)}}^{2}}}}=\frac{{(-x+4)x}}{{{{{\left[ {-(-x+2)} \right]}}^{2}}}}=\frac{{(4-x)x}}{{{{{(-1)}}^{2}}{{{(2-x)}}^{2}}}}=\frac{{(4-x)x}}{{{{{(2-x)}}^{2}}}}$
  
  No i wyszedł Pani wynik 🙂
2. Karolina
  14 września 2016 at 13:59
  
  jeju, rzeczywiście, ale głupi błąd! 😛
  Bardzo dziękuje, juz rozumiem 😉
Julia
20 czerwca 2016 at 16:22

Witam, nie rozumiem dlaczego pochodna ln2x^2 to y'(x) = (2 log(2 x))/x

Odpowiedz
Matematyk
31 maja 2016 at 12:16

Bardzo pomocny kalkulator pochodnych funkcji, przydatny szczególnie do sprawdzania wyników.

Odpowiedz
Paulina
18 maja 2016 at 11:20

Witam 🙂 Dlaczego pochodna z e^(2^x)=2^x*e^(2^x)*log2?

Odpowiedz
1. Joanna Grochowska
  14 lutego 2017 at 11:21
  
  Tutaj jest do policzenia pochodna funkcji złozonej, czyli argumentem nie jest sam „x” tylko coś więcej, nie ma po prostu $e to the power of x$ tylko $e to the power of c o ś end exponent$ .
  Postępujemy jak zawsze w takich przypadkach, czyli: pochodna tego co „na zewnątrz” pomnożyć razy pochodna funkcji wewnętrznej (coś więcej niż sam „x”), czyli jakby $open parentheses e to the power of increment close parentheses apostrophe equals e to the power of increment times increment apostrophe$
  
  Stąd: $open parentheses e to the power of 2 to the power of x end exponent close parentheses apostrophe equals e to the power of 2 to the power of x end exponent times open parentheses 2 to the power of x close parentheses apostrophe equals e to the power of 2 to the power of x end exponent times 2 to the power of x times ln 2$ , gdyż wprost z wzorku $open parentheses a to the power of x close parentheses apostrophe equals a to the power of x times ln a$ .
studentekonomi
13 marca 2016 at 20:47

Witam. Mam problem z zadaniem: f(x1,x2)=1/2ln(5×1^2-2×2). Jak mogę narysować krzywe w punktach 0, 1 i 2? Wytyczenie pochodnej i całki również by się przydało…

Odpowiedz
Iulia
13 lutego 2016 at 15:13

Dzień dobry, bardzo prosiłabym o pomóc z przykładem [((arctgX^2)^3)/((e^3)*x+3^x)]^(arctg(x^4-ln(2x^8+1) Czyli iloraz w tym kwadratowym nawiasie podnosimy do potęgi i z tego wszystkiego policzyć pochodną…wychodzą mi kosmiczne rozwiazania…Z góry dziękuję.

Odpowiedz
Kasia
4 lutego 2016 at 12:07

Panie Krystianie,
może jest mi Pan w stanie wytłumaczyć dlaczego pochodna z -arctg|x| ma pochodną -x/(|x^3|+|x|), a nie po prostu -1/(1+x^2)?

Byłabym bardzo wdzięczna za pomoc 🙂

Odpowiedz
1. Joanna Grochowska
  10 lutego 2016 at 09:57
  
  Pani Kasiu, gdyby do policzenia byłaby pochodna po prostu z $\displaystyle -arctgx$ to byłaby równa rzeczywiście $\displaystyle -\frac{1}{{1+{{x}^{2}}}}$
  
  Jednak tutaj do policzenia jest pochodna $\displaystyle -arctg\left| x \right|$ , czyli argumentem nie jest sam „x” tylko coś więcej – moduł z „x”.
  
  Postępujemy jak zawsze w takich przypadkach, czyli: pochodna tego co „na zewnątrz” pomnożyć razy pochodna funkcji wewnętrznej (coś więcej niż sam „x”), czyli jakby $\displaystyle \left( {-arctg\Delta } \right)'\cdot \Delta '$
  
  Pytanie, ile wynosi pochodna modułu z x ?
  
  Rozpisując moduł, wiem, że:
  $open vertical bar x close vertical bar equals open curly brackets table attributes columnalign \left end attributes row cell x comma space space space space space space space space x greater or equal than 0 end cell row cell negative x comma space space space space space x less than 0 end cell end table close$
  
  Czyli odpowiednio pochodna byłby równa 1 lub -1.. Jednak potrzebuję pochodnej w ogólnym przypadku (nie na przedziałach).
  
  Dlatego uznaje się, że pochodna modułu to (warto zapamiętać ten wzór):
  
  $\displaystyle \left( {\left| x \right|} \right)'=\frac{x}{{\left| x \right|}}$
  
  Można sobie rozpisać na odpowiednich przedziałach i faktycznie wyjdzie 1 lub -1 😉
  
  Mając wszystko, liczę:
  
  $\displaystyle \left( {-arctg\left| x \right|} \right)'=-\frac{1}{{1+{{{\left| x \right|}}^{2}}}}\cdot \left( {\left| x \right|} \right)'=-\frac{1}{{1+{{{\left| x \right|}}^{2}}}}\cdot \frac{x}{{\left| x \right|}}=-\frac{x}{{\left| x \right|+{{{\left| x \right|}}^{3}}}}$
Kamil
4 lutego 2016 at 10:15

Mam wielką prośbę. Nie moge poradzić sobie z monotonicznością tej funkcji x^3/(x^2+-x-2) będę ogromnie wdzięczny za odpowiedz. Pozdrawiam 🙂

Odpowiedz
1. Kamil
  4 lutego 2016 at 10:17
  
  x^3/(x^2-x-2) wyzej jest mały bląd
2. Anna Zalewska
  1 listopada 2016 at 01:14
  
  Dana jest funkcja $f \left parenthesis x \right parenthesis equals fraction numerator x cubed over denominator x squared minus x minus 2 end fraction$ .
  
  Zaczynamy od wyznaczenia dziedziny funkcji.
  
  $x squared minus x minus 2 not equal to 0$
  $capital delta equals \left parenthesis negative 1 \right parenthesis squared minus 4 times 1 times \left parenthesis negative 2 \right parenthesis equals 9$
  $x subscript 1 equals fraction numerator 1 minus square root of 9 over denominator 2 end fraction equals fraction numerator 1 minus 3 over denominator 2 end fraction equals fraction numerator negative 2 over denominator 2 end fraction equals negative 1$
  $space x subscript 2 equals fraction numerator 1 plus square root of 9 over denominator 2 end fraction equals fraction numerator 1 plus 3 over denominator 2 end fraction equals 4 over 2 equals 2$
  
  Zatem $D equals straight real numbers \backslash \left curly bracket negative 1 comma 2 \right curly bracket$ .
  
  Przechodzimy do wyznaczania monotoniczności funkcji $f$ . W tym celu obliczymy jej pochodną i sprawdzimy, kiedy jest dodatnia, a kiedy ujemna.
  
  $f apostrophe \left parenthesis x \right parenthesis equals fraction numerator open parentheses x cubed close parentheses apostrophe times open parentheses x squared minus x minus 2 close parentheses minus x cubed times open parentheses x squared minus x minus 2 close parentheses apostrophe over denominator open parentheses x squared minus x minus 2 close parentheses squared end fraction equals$
  $equals fraction numerator 3 x squared times open parentheses x squared minus x minus 2 close parentheses minus x cubed times open parentheses 2 x minus 1 close parentheses over denominator open parentheses x squared minus x minus 2 close parentheses squared end fraction equals fraction numerator 3 x to the power of 4 minus 3 x cubed minus 6 x squared minus 2 x to the power of 4 plus x cubed over denominator open parentheses x squared minus x minus 2 close parentheses squared end fraction equals$
  $equals fraction numerator x to the power of 4 minus 2 x cubed minus 6 x squared over denominator open parentheses x squared minus x minus 2 close parentheses squared end fraction$
  
  Zbadamy teraz, kiedy pochodna przyjmuje wartości większe lub równe $0$ , a kiedy mniejsze lub równe $0$ .
  
  $fraction numerator x to the power of 4 minus 2 x cubed minus 6 x squared over denominator open parentheses x squared minus x minus 2 close parentheses squared end fraction greater or equal than 0$
  
  $x to the power of 4 minus 2 x cubed minus 6 x squared greater or equal than 0$
  
  $x squared open parentheses x squared minus 2 x minus 6 close parentheses greater or equal than 0$
  
  $capital delta subscript 1 equals \left parenthesis negative 2 \right parenthesis squared minus 4 times 1 times \left parenthesis negative 6 \right parenthesis equals 28$
  $x subscript 1 equals fraction numerator 2 minus square root of 28 over denominator 2 end fraction equals fraction numerator 2 minus 2 square root of 7 over denominator 2 end fraction equals 1 minus square root of 7$
  $x subscript 2 equals fraction numerator 2 plus square root of 28 over denominator 2 end fraction equals fraction numerator 2 plus 2 square root of 7 over denominator 2 end fraction equals 1 plus square root of 7$
  
  Pochodna przyjmuje wartości większe lub równe $0$ dla $x element of \left parenthesis negative infinity comma 1 minus square root of 7 greater than$ oraz dla $x element of less than 1 plus square root of 7 comma space plus infinity \right parenthesis$ .
  Pochodna przyjmuje wartości mniejsze lub równe $0$ dla $x element of less than 1 minus square root of 7 comma 1 plus square root of 7 greater than$ .
  
  Należy pamiętać o założeniach dziedziny: $D equals straight real numbers \backslash \left curly bracket negative 1 comma 2 \right curly bracket$ .
  
  Zatem podana funkcja jest rosnąca w przedziałach $x element of \left parenthesis negative infinity comma 1 minus square root of 7 greater than$ , $x element of less than 1 plus square root of 7 comma space plus infinity \right parenthesis$ oraz malejąca w przedziałach $x element of less than 1 minus square root of 7 comma negative 1 \right parenthesis$ , $x element of open parentheses negative 1 comma 2 close parentheses$ , $x element of \left parenthesis 2 comma space 1 plus square root of 7 greater than$ .
Klaudia
1 lutego 2016 at 17:30

Witam! Mam taką funkcję :
f(x) = (2x-x^2)^(2/3). Jak obliczyć pochodną takiej funkcji?

Odpowiedz
1. Joanna Grochowska
  2 lutego 2016 at 16:37
  
  By obliczyć pochodną z funkcji $\displaystyle {{(2x-{{x}^{2}})}^{{\frac{2}{3}}}}$ stosuję wzór
  
  $\displaystyle \left( {{{x}^{n}}} \right)'=n\cdot {{x}^{{n-1}}}$ , gdzie jak zauważam, mam coś więcej niż sam „x”, mam dodatkową funkcję (zwaną funkcją wewnętrzną). W taki przypadku obliczoną pochodną przemnażamy przez pochodną funkcji wewnętrznej, czyli mam jakby:
  
  $\displaystyle \left( {{{\Delta }^{n}}} \right)'=n\cdot {{\Delta }^{{n-1}}}\cdot \Delta '$
  
  Mam więc:
  \displaystyle \left( {{{{(2x-{{x}^{2}})}}^{{\frac{2}{3}}}}} \right)’=\frac{2}{3}{{(2x-{{x}^{2}})}^{{\frac{2}{3}-1}}}\cdot (2x-{{x}^{2}})’=\frac{2}{3}{{(2x-{{x}^{2}})}^{{-\frac{1}{3}}}}\cdot (2-2x)=\frac{{2\cdot (2-2x)}}{{3\sqrt[3]{{2x-{{x}^{2}}}}}}[/latex]
Karim
30 stycznia 2016 at 11:40

Witam wszystkich. I proszę o pomoc.
Mam problem z taką pochodną
f(x)=[1-sin(2x)]/[2x^4+7x^2-3] Zatrzymuje się w pewnym momencie i nie wiem co dalej. Kalkulator do pochodnych stworzonego przez Pana Krystiana błędnie odczytuje ostatnia część 7x^2-3 zamiast zrobić wszystko w potędze obejmuje liczbę trzy od reszty za potęga. Proszę o pomoc

Odpowiedz
1. Joanna Grochowska
  1 lutego 2016 at 13:49
  
  To nie chodzi Panu o pochodną funkcji $\displaystyle \frac{{1-sin(2x)}}{{2{{x}^{4}}+7{{x}^{2}}-3}}$ ?
  
  A może $\displaystyle \frac{{1-sin(2x)}}{{2{{x}^{4}}+{{7}^{{{{x}^{2}}-3}}}}}$ , czy jeszcze inaczej? Proszę może gdzieś nawias () wstawić dodatkowo, to co ma być ujęte w potędze, bo nie do końca rozumiem o co chodzi z
  „część 7x^2-3 zamiast zrobić wszystko w potędze obejmuje liczbę trzy od reszty za potęga”.
  
  Pozdrawiam
aga
28 stycznia 2016 at 22:53

Witam, mam problem z pochodną: e^(3x+2)*((x^6)+4). Nie mam pojęcia jak to rozwiązać, bardzo proszę o pomoc…

Odpowiedz
1. Joanna Grochowska
  3 lutego 2016 at 10:32
  
  Wykorzystuję tutaj wzór na iloczyn dwóch funkcji
  
  $\displaystyle \left( {f\cdot g} \right)'=f'\cdot g+f\cdot g'$
  
  Muszę również pamiętać o tym, że licząc pochodną funkcji złożonej, muszę domnożyć jeszcze razy pochodna funkcji wewnętrznej, tego „coś więcej niż sam x” . to znaczy
  
  $\displaystyle \left( {{{e}^{\Delta }}} \right)'={{e}^{\Delta }}\cdot \Delta '$
  
  No to rozwiązując przykład:
  $\displaystyle \begin{matrix}\left( {{{e}^{{3x+2}}}\cdot ({{x}^{6}}+4)} \right)'=\left( {{{e}^{{3x+2}}}} \right)'\cdot ({{x}^{6}}+4)+{{e}^{{3x+2}}}\cdot ({{x}^{6}}+4)'= \\ {{e}^{{3x+2}}}\cdot (3x+2)'\cdot ({{x}^{6}}+4)+{{e}^{{3x+2}}}\cdot (6{{x}^{5}}+0)={{e}^{{3x+2}}}\cdot 3\cdot ({{x}^{6}}+4)+{{e}^{{3x+2}}}\cdot 6{{x}^{5}}= \\ 3{{e}^{{3x+2}}}\cdot \left( {{{x}^{6}}+4+2{{x}^{5}}} \right)=3{{e}^{{3x+2}}}\cdot \left( {{{x}^{6}}+2{{x}^{5}}+4} \right)\end{matrix}$
Andzia
28 stycznia 2016 at 22:50

Pochodna z: cos^2\pierwiastek z x +sin^2\pierwiastek z x.

Odpowiedz
1. Joanna Grochowska
  3 lutego 2016 at 11:25
  
  Czyli chodzi o pochodną funkcji $\displaystyle {{cos }^{2}}\sqrt{x}+{{sin }^{2}}\sqrt{x}$ ?
  
  No to liczę:
  $\displaystyle \begin{matrix}\left( {{{{cos }}^{2}}\sqrt{x}+{{{sin }}^{2}}\sqrt{x}} \right)'=2cos \sqrt{x}\cdot \left( {cos \sqrt{x}} \right)'+2sin \sqrt{x}\cdot \left( {sin \sqrt{x}} \right)'= \\ 2cos \sqrt{x}\cdot (-sin \sqrt{x})\cdot \left( {\sqrt{x}} \right)'+2sin \sqrt{x}\cdot cos \sqrt{x}\cdot \left( {\sqrt{x}} \right)'= \\-2sin \sqrt{x}cos \sqrt{x}\cdot \frac{1}{{2\sqrt{x}}}+2sin \sqrt{x}\cdot cos \sqrt{x}\cdot \frac{1}{{2\sqrt{x}}}=0\end{matrix}$
Misia
28 stycznia 2016 at 17:59

Dzień dobry panie Krystianie, czy mogłabym liczyć na pomoc w policzeniu pochodnej e^-x^2
Z góry dziękuję i pozdrawiam

Odpowiedz
1. Joanna Grochowska
  19 lutego 2016 at 12:59
  
  Pochodna funkcji $\displaystyle y={{e}^{-}}^{{{{x}^{2}}}}$
  
  Jest to funkcja złożona, licząc jej pochodną, liczę pochodną funkcji „zewnętrznej”, czyli e^(coś) i muszę domnożyć jeszcze ją razy pochodna funkcji wewnętrznej, tego „coś więcej niż sam x” . to znaczy
  
  $\displaystyle \left( {{{e}^{\Delta }}} \right)'={{e}^{\Delta }}\cdot \Delta '$
  
  Mam:
  
  $\displaystyle \left( {{{e}^{-}}^{{{{x}^{2}}}}} \right)'={{e}^{-}}^{{{{x}^{2}}}}\cdot \left( {-{{x}^{2}}} \right)'={{e}^{-}}^{{{{x}^{2}}}}\cdot \left( {-2x} \right)=-2x{{e}^{-}}^{{{{x}^{2}}}}$
ela
19 stycznia 2016 at 19:55

Witam a jak to rozwiązać ? :/ (x+1)(x+4)

Odpowiedz
1. Joanna Grochowska
  1 lutego 2016 at 13:14
  
  f(x)=(x+1)(x+4)
  
  Pochodną tego można policzyć tak na prawdę na dwa sposoby:
  
  I SPOSÓB – z pochodnej iloczynu $\displaystyle \left( {f\cdot g} \right)'=f'\cdot g+f\cdot g'$
  
  $\displaystyle \begin{matrix}\left( {\text{(x+1)(x+4)}} \right)\text{ }!!'!!\text{ =(x+1) }!!'!!\text{ }\cdot \text{(x+4)}+\text{(x+1)}\cdot \text{(x+4) }!!'!!\text{ =(1+0)}\cdot \text{(x+4)}+\text{(x+1)}\cdot \text{(1+0)=}\text{x+4+x+1=2x+5}\end{matrix}$
  
  II SPOSÓB – przemnożyć przez siebie te dwa nawiasy (bez problemu mogę, gdyż w jednym jak i w drugim jest wielomian) i potem policzyć pochodną otrzymanego wielomianu korzystając z wzoru $\displaystyle \left( {{{x}^{n}}} \right)'=n\cdot {{x}^{{n-1}}}$
  
  $\displaystyle \text{(x+1)(x+4)}={{x}^{2}}+4x+x+4={{x}^{2}}+5x+4$
  
  $\displaystyle \left( {{{x}^{2}}+5x+4} \right)'=\left( {{{x}^{2}}} \right)'+\left( {5x} \right)'+\left( 4 \right)'=2x+5\cdot 1+0=2x+5$
Lidka
17 stycznia 2016 at 03:45

Witam Panie Krystianie. Czy w wyznaczaniu pochodnych takie cos jak: e^pi , traktujemy jako liczbę czyli wynik to zero czy w inny sposób?

Dziękuje za odpowiedz
Pozdrawiam

Odpowiedz
1. Joanna Grochowska
  18 stycznia 2016 at 08:51
  
  Tak dokładnie, traktujemy to wyrażenie jako liczbę (nie ma Pani tutaj żadnej zmiennej „x”, tylko same stałe), więc pochodna tego to zero 🙂
Mariusz Wysocki
11 stycznia 2016 at 20:02

Czy ktoś by mógł mi pomóc w rozwiązaniu tych pochodnych?

y=e^(1/cosx)
y=a/2(e^(x/a)+e^(-(x/a)))
y=arcsin(e^4x )
y=e^√(7x^2 )
y=log_7cos√(1+x)

Odpowiedz
1. Joanna Grochowska
  22 lutego 2016 at 15:39
  
  Przykład pierwszy: $\displaystyle y={{e}^{{\frac{1}{{cos x}}}}}$
  
  Jest to funkcja złożona, liczę pochodną funkcji „zewnętrznej”, czyli e^(coś) i muszę domnożyć jeszcze ją razy pochodna funkcji wewnętrznej, tego „coś więcej niż sam x” . To znaczy
  
  $\displaystyle \left( {{{e}^{\Delta }}} \right)'={{e}^{\Delta }}\cdot \Delta '$
  
  Mam:
  $\displaystyle \left( {{{e}^{{\frac{1}{{cos x}}}}}} \right)'={{e}^{{\frac{1}{{cos x}}}}}\cdot \left( {\frac{1}{{cos x}}} \right)'$
  
  Pochodną $\displaystyle \left( {\frac{1}{{cos x}}} \right)'$ można policzyć np z wzoru na iloraz dwóch funkcji
  $\displaystyle \left( {\frac{f}{g}} \right)'=\frac{{f'\cdot g-f\cdot g'}}{{{{g}^{2}}}}$
  
  ${e^{\frac{1}{{\cos x}}}}\frac{{1' \cdot \cos x – 1 \cdot {{\left( {\cos x} \right)}^\prime }}}{{{{\cos }^2}x}} = {e^{\frac{1}{{\cos x}}}}\frac{{ – \left( { – \sin x} \right)}}{{{{\cos }^2}x}} = \frac{{{e^{\frac{1}{{\cos x}}}}\sin x}}{{{{\cos }^2}x}}$
2. Joanna Grochowska
  3 marca 2016 at 15:29
  
  Przykład drugi: $\displaystyle y=\frac{a}{2}({{e}^{{^{{\frac{x}{a}}}}}}+{{e}^{{-\frac{x}{a}}}})$
  
  Jak rozumiem, liczbę „a” traktuję jako pewną stałą?
  
  No to liczę pochodną, stosując wzór: $\displaystyle \left( {{{e}^{\Delta }}} \right)'={{e}^{\Delta }}\cdot \Delta '$
  
  $\displaystyle y'=\left( {\frac{a}{2}({{e}^{{^{{\frac{x}{a}}}}}}+{{e}^{{-\frac{x}{a}}}})} \right)'=\frac{a}{2}\left( {{{e}^{{^{{\frac{x}{a}}}}}}+{{e}^{{-\frac{x}{a}}}}} \right)'=\frac{a}{2}\left[ {\left( {{{e}^{{^{{\frac{x}{a}}}}}}} \right)'+\left( {{{e}^{{-\frac{x}{a}}}}} \right)'} \right]=$
  $\displaystyle \frac{a}{2}\left[ {{{e}^{{^{{\frac{x}{a}}}}}}\left( {\frac{x}{a}} \right)'+{{e}^{{^{{-\frac{x}{a}}}}}}\left( {-\frac{x}{a}} \right)'} \right]=\frac{a}{2}\left[ {{{e}^{{^{{\frac{x}{a}}}}}}\cdot \frac{1}{a}\cdot 1+{{e}^{{^{{-\frac{x}{a}}}}}}\cdot \left( {-\frac{1}{a}} \right)\cdot 1} \right]=$
  $\displaystyle \frac{a}{2}\cdot \frac{1}{a}\left( {{{e}^{{^{{\frac{x}{a}}}}}}-{{e}^{{^{{-\frac{x}{a}}}}}}} \right)=\frac{1}{2}\left( {{{e}^{{^{{\frac{x}{a}}}}}}-{{e}^{{^{{-\frac{x}{a}}}}}}} \right)$
  
  Można ewentualnie trochę przekształcić wynik i otrzymać:
  $\displaystyle \frac{1}{2}\left( {{{e}^{{^{{\frac{x}{a}}}}}}-{{e}^{{^{{-\frac{x}{a}}}}}}} \right)=\frac{1}{2}\left( {{{e}^{{^{{\frac{{2x}}{a}-\frac{x}{a}}}}}}-{{e}^{{^{{-\frac{x}{a}}}}}}} \right)=\frac{1}{2}{{e}^{{^{{-\frac{x}{a}}}}}}\left( {{{e}^{{^{{\frac{{2x}}{a}}}}}}-1} \right)$
3. Joanna Grochowska
  4 marca 2016 at 13:50
  
  Przykład trzeci: chodzi o $\displaystyle y=arcsin({{e}^{4}}\cdot x)$ czy może $\displaystyle y=arcsin({{e}^{{4x}}})$
  
  Pierwszy przypadek:
  
  $\displaystyle \left( {arcsin({{e}^{4}}\cdot x)} \right)'=\frac{1}{{\sqrt{{1-{{{({{e}^{4}}\cdot x)}}^{2}}}}}}\cdot \left( {{{e}^{4}}\cdot x} \right)'=\frac{1}{{\sqrt{{1-{{{({{e}^{4}}\cdot x)}}^{2}}}}}}\cdot {{e}^{4}}\left( x \right)'=\frac{{{{e}^{4}}}}{{\sqrt{{1-{{e}^{8}}{{x}^{2}}}}}}$
  
  Drugi przypadek:
  
  $\displaystyle \left( {arcsin({{e}^{{4x}}})} \right)'=\frac{1}{{\sqrt{{1-{{{({{e}^{{4x}}})}}^{2}}}}}}\cdot \left( {{{e}^{{4x}}}} \right)'=\frac{1}{{\sqrt{{1-{{e}^{{8x}}}}}}}\cdot {{e}^{{4x}}}\left( {4x} \right)'=\frac{{4{{e}^{{4x}}}}}{{\sqrt{{1-{{e}^{{8x}}}}}}}$
4. Joanna Grochowska
  21 marca 2016 at 12:53
  
  Przykład czwarty: $\displaystyle y={{e}^{{\sqrt{{7{{x}^{2}}}}}}}$
  
  Mamy tutaj złożenie kilku funkcji, dlatego korzystam z następujących wzorów:
  
  $\displaystyle \left( {{{e}^{\Delta }}} \right)'={{e}^{\Delta }}\cdot \Delta '$
  
  $\displaystyle \left( {\sqrt{\Delta }} \right)'=\frac{1}{{2\sqrt{\Delta }}}\cdot \Delta '$
  
  gdzie znaczek $\displaystyle \Delta$ oznacza po prostu „coś więcej niż sam x”.
  
  $\displaystyle y'=\left( {{{e}^{{\sqrt{{7{{x}^{2}}}}}}}} \right)'={{e}^{{\sqrt{{7{{x}^{2}}}}}}}\cdot \left( {\sqrt{{7{{x}^{2}}}}} \right)'={{e}^{{\sqrt{{7{{x}^{2}}}}}}}\cdot \frac{1}{{2\sqrt{{7{{x}^{2}}}}}}\cdot \left( {7{{x}^{2}}} \right)'=\frac{{{{e}^{{\sqrt{{7{{x}^{2}}}}}}}}}{{2\sqrt{{7{{x}^{2}}}}}}\cdot 7\cdot 2x=\frac{{7x{{e}^{{\sqrt{{7{{x}^{2}}}}}}}}}{{\sqrt{{7{{x}^{2}}}}}}$
5. Joanna Grochowska
  23 marca 2016 at 07:59
  
  Przykład piąty: $\displaystyle lo{{g}_{7}}cos\sqrt{{1+x}}$
  
  Tym razem mamy pochodną logarytmu, gdzie pod wyrażeniem logarytmowanym jest coś więcej niż sam x (oznaczam to przez $\displaystyle \Delta$ ). Funkcja jest złożona i to kilkukrotnie. Dlatego stosuję na początku wzór :
  
  $\displaystyle \left( {{{{log }}_{a}}\Delta } \right)'=\frac{1}{{\Delta ln a}}\cdot \Delta'$
  
  Obliczając kolejne pochodne, Mam więc:
  
  $\displaystyle \left( {{{{log }}_{7}}cos \sqrt{{1+x}}} \right)'=\frac{1}{{cos \sqrt{{1+x}}\cdot ln 7}}\cdot \left( {cos \sqrt{{1+x}}} \right)'=$
  
  $\displaystyle \frac{1}{{cos \sqrt{{1+x}}\cdot ln 7}}\cdot \left( {-sin \sqrt{{1+x}}} \right)\cdot \left( {\sqrt{{1+x}}} \right)'=$
  
  $\displaystyle -\frac{{sin \sqrt{{1+x}}}}{{cos \sqrt{{1+x}}\cdot ln 7}}\cdot \frac{1}{{2\sqrt{{1+x}}}}\cdot \left( {1+x} \right)'=$
  
  $\displaystyle -tg\sqrt{{1+x}}\cdot \frac{1}{{2\cdot ln 7\cdot \sqrt{{1+x}}}}\cdot \left( {0+1} \right)=-\frac{{tg\sqrt{{1+x}}}}{{2ln 7\cdot \sqrt{{1+x}}}}$
paulina
5 stycznia 2016 at 12:30

dlaczego pochodna z -x/(x-1)^2 wychodzi y'(x) = (x+1)/(x-1)^3

Odpowiedz
1. Joanna Grochowska
  7 stycznia 2016 at 15:30
  
  Stosuję tutaj wzór na pochodną ilorazu dwóch funkcji, czyli
  $\displaystyle \left( {\frac{f}{g}} \right)'=\frac{{f'\cdot g-f\cdot g'}}{{{{g}^{2}}}}$
  
  No to rozpisując przykład:
  $\displaystyle \left( {\frac{{-x}}{{{{{(x-1)}}^{2}}}}} \right)'=\frac{{\left( {-x} \right)'\cdot {{{(x-1)}}^{2}}-\left( {-x} \right)\cdot \left[ {{{{(x-1)}}^{2}}} \right]'}}{{{{{\left[ {{{{(x-1)}}^{2}}} \right]}}^{2}}}}=\frac{{\left( {-1} \right)\cdot {{{(x-1)}}^{2}}+x\cdot 2\cdot (x-1)\cdot (x-1)'}}{{{{{(x-1)}}^{4}}}}=\frac{{-{{{(x-1)}}^{2}}+2x\cdot (x-1)\cdot 1}}{{{{{(x-1)}}^{4}}}}=\frac{{(x-1)\cdot \left[ {-(x-1)+2x} \right]}}{{{{{(x-1)}}^{4}}}}=\frac{{-x+1+2x}}{{{{{(x-1)}}^{3}}}}=\frac{{x+1}}{{{{{(x-1)}}^{3}}}}$
Tomek
5 grudnia 2015 at 19:58

Cześć
Mam prośbę w sprawie rozwiązania równania różniczkowego metodą analityczną (krok po kroku):
y`-0,5y=xe^(2x)
z góry dziękuję

Odpowiedz
dominika
15 listopada 2015 at 16:08

Chciałabym dowiedzieć się jak wyszedł ten wynik:y'(x) = 3 x^2 cos(1-x^2)+2 x^4 sin(1-x^2) z funkcji x^3cos(x^2-1)

Odpowiedz
1. Joanna Grochowska
  8 stycznia 2016 at 14:56
  
  Tutaj by obliczyć pochodną podanej funkcji, wykorzystuję wzór na pochodną iloczynu dwóch funkcji:
  $\displaystyle \left( {f\cdot g} \right)'=f'\cdot g+f\cdot g'$
  
  Jedną z niech jest $\displaystyle f={{x}^{3}}$ , drugą zaś $\displaystyle g=cos ({{x}^{2}}-1)$ , która jest funkcją złożoną.
  
  No to liczymy pochodną:
  $\displaystyle \left( {{{x}^{3}}cos ({{x}^{2}}-1)} \right)'=\left( {{{x}^{3}}} \right)'\cdot \left( {cos ({{x}^{2}}-1)} \right)+\left( {{{x}^{3}}} \right)\cdot \left( {cos ({{x}^{2}}-1)} \right)'=3{{x}^{2}}\cdot cos ({{x}^{2}}-1)+{{x}^{3}}\cdot \left( {-sin ({{x}^{2}}-1)} \right)\cdot ({{x}^{2}}-1)'=3{{x}^{2}}\cdot cos ({{x}^{2}}-1)-{{x}^{3}}\cdot sin ({{x}^{2}}-1)\cdot 2x=3{{x}^{2}}\cdot cos ({{x}^{2}}-1)-2{{x}^{4}}\cdot sin ({{x}^{2}}-1)$
  
  Wynik jest jednak odrobinę inny od tego wskazanego w WolframAlpha
  http://www.wolframalpha.com/input/?i=%28x%5E3*cos%28x%5E2-1%29%29%27
  
  Widać, że wyrażenie w nawiasie – wielomian jest przedstawiony „odwrotnie”, jakby z minusem, co oczywiście można zrobić, czyli $\displaystyle cos ({{x}^{2}}-1)=cos (-(1-{{x}^{2}}))$ lub też $\displaystyle sin ({{x}^{2}}-1)=sin (-(1-{{x}^{2}}))$
  I w tym miejscu korzystając z własności funkcji trygonometrycznych kąta ujemnego:
  $\displaystyle \begin{matrix} cos (-\alpha )=cos (\alpha )sin (-\alpha )=-sin (\alpha )\end{matrix}$
  
  Otrzymuję wynik zgodny z tym wskazanym z kalkulatorze:
  $\displaystyle 3{{x}^{2}}\cdot cos ({{x}^{2}}-1)-2{{x}^{4}}\cdot sin ({{x}^{2}}-1)=3{{x}^{2}}\cdot cos (-(-{{x}^{2}}+1))-2{{x}^{4}}\cdot sin (-(-{{x}^{2}}+1))=3{{x}^{2}}\cdot cos (1-{{x}^{2}})-2{{x}^{4}}\cdot (-sin (1-{{x}^{2}}))=3{{x}^{2}}\cdot cos (1-{{x}^{2}})+2{{x}^{4}}\cdot sin (1-{{x}^{2}})$
Karol
9 września 2015 at 15:39

Witam. Dostałem na egzaminie dwa przykłady, skorzystałem z kalkulatora on je oczywiście obliczył ale ja nadal nie wiem skąd wziął się wynik, oto one :
1) (niestety nie wiem do czego dąży x bo się zamazało ale chyba do nieskończoności) lim(lm(1+4x^2))/x
2) (też x chyba dąży do nieskończoności) lim(1-e^2x)/tg(x)
Pozdrawiam Karol

Odpowiedz
Marlena
11 kwietnia 2015 at 21:06

Dzień dobry.
Pewnie pisze pod złym postem, forum, czy nie wiem jak to nazwać. Jednakże mam zadanie które nie bardzo wiem, jak rozwiązać. Liczę na Pańską pomoc 🙂

Zad.: Dowieść,że dla xcR prawdziwa jest nierówność:
a) 2xarctgx > ln(1+x^2)
b) |arctgx – arctgy| <= |x-y|

Dodam jeszcze, iż wiem, że jest to związane z Twierdzeniem Lagrange'a ale nawet z tą wiedzą nic mądrego mi nie wychodzi 🙁

Odpowiedz
Anna
30 stycznia 2015 at 16:18

Dzień dobry!

Muszę policzyć pierwszą i drugą pochodną z y=lnx/√x wygląda niewinnie ale jest niezwykle uciążliwa. Bardzo proszę o pomoc Panie Krystianie

Odpowiedz
1. Kamil Kocot
  22 października 2016 at 19:34
  
  $y equals fraction numerator ln x over denominator square root of x end fraction$
  
  Należy skorzystać ze wzoru na dzielenie
  
  $open parentheses f over g close parentheses to the power of apostrophe equals fraction numerator f apostrophe g minus f g apostrophe over denominator g squared end fraction$
  
  Dostaniemy
  
  $table attributes columnalign \right center \left columnspacing 0px end attributes row cell y apostrophe end cell equals cell fraction numerator open parentheses ln x close parentheses apostrophe times square root of x minus ln x times open parentheses square root of x close parentheses apostrophe over denominator open parentheses square root of x close parentheses squared end fraction equals fraction numerator \begin display style 1 over x end style times square root of x minus ln x times \begin display style fraction numerator 1 over denominator 2 square root of x end fraction end style over denominator x end fraction end cell row blank equals cell fraction numerator \begin display style fraction numerator square root of x over denominator x end fraction minus fraction numerator ln x over denominator 2 square root of x end fraction end style over denominator x end fraction times fraction numerator 2 square root of x over denominator 2 square root of x end fraction equals fraction numerator \begin display style fraction numerator 2 x over denominator x end fraction minus ln x end style over denominator 2 x square root of x end fraction end cell row blank equals cell fraction numerator \begin display style 2 minus ln x end style over denominator 2 x square root of x end fraction end cell end table$
  
  I druga pochodna
  
  $table attributes columnalign \right center \left columnspacing 0px end attributes row cell y apostrophe apostrophe end cell equals cell open parentheses fraction numerator \begin display style 2 minus ln x end style over denominator 2 x square root of x end fraction close parentheses to the power of apostrophe equals fraction numerator \begin display style open parentheses 2 minus ln x close parentheses apostrophe times 2 x square root of x minus open parentheses 2 minus ln x close parentheses times open parentheses 2 x square root of x close parentheses apostrophe end style over denominator open parentheses 2 x square root of x close parentheses squared end fraction end cell row blank equals cell fraction numerator \begin display style open parentheses negative 1 over x close parentheses times 2 x square root of x minus open parentheses 2 minus ln x close parentheses times open parentheses 2 x to the power of bevelled 3 over 2 end exponent close parentheses apostrophe end style over denominator open parentheses 2 x to the power of \begin display style bevelled 3 over 2 end style end exponent close parentheses squared end fraction end cell row blank equals cell fraction numerator \begin display style open parentheses negative 1 over x close parentheses times 2 x square root of x minus open parentheses 2 minus ln x close parentheses times 2 times 3 over 2 x to the power of bevelled 1 half end exponent end style over denominator 4 x cubed end fraction end cell row blank equals cell fraction numerator \begin display style negative 2 square root of x minus open parentheses 2 minus ln x close parentheses times 3 square root of x end style over denominator 4 x cubed end fraction end cell row blank equals cell fraction numerator \begin display style negative 2 square root of x minus 6 square root of x plus 3 square root of x ln x end style over denominator 4 x cubed end fraction end cell row blank equals cell fraction numerator \begin display style negative 8 square root of x plus 3 square root of x ln x end style over denominator 4 x cubed end fraction end cell row blank equals cell fraction numerator \begin display style square root of x open parentheses 3 minus 8 ln x close parentheses end style over denominator 4 x cubed end fraction end cell row blank equals cell fraction numerator \begin display style 3 minus 8 ln x end style over denominator 4 x squared square root of x end fraction end cell end table$
Tomasz W.
29 stycznia 2015 at 16:42

Witam. Mam problem z obliczeniem pochodnej dla f(x) = arcsin√1-x/1+x. Całe wyrażenie dzielenia jest pod pierwiastkiem.

Odpowiedz
damian
29 stycznia 2015 at 12:45

y=e^2x + x^2 + cos(4x^3-6)

przy e jest do potęgi 2x.

potrzebuje pomocy

Odpowiedz
Aleksandra K.
11 stycznia 2015 at 20:06

A dlaczego pochodna z ctgx+x=-ctg^2x ????????????

Odpowiedz
pilarczyk123
13 listopada 2014 at 20:03

chcialbym zapytac jako co traktujemy a/t przy funkcji cos t/a

Odpowiedz
Paulina
12 listopada 2014 at 20:41

Mam pytanie
dlaczego √x(1-2x^2) ma pochodną 1-10x^2/2√x ? Prosze o wytłumaczenie. Z gódy dziękuje 🙂

Odpowiedz
Kasia
4 listopada 2014 at 20:42

Pomoże ktoś mam do obliczenia 2 pochodne : (sinx / sinx-cosx) i pierwiastek z 5 tgx -2ctgx. Z góry dziękuje za odpowiedź 🙂

Odpowiedz
Karolina
1 września 2014 at 14:25

Dzień dobry, jak policzyć pochodną (x-1)^3(x-2) krok po kroku i dlaczego wyznacza się 3 przed nawias? Nie rozumiem tego. Byłabym wdzięczna za wytłumaczenie. Pozdrawiam

Odpowiedz
KASIA
31 sierpnia 2014 at 16:29

pochodna sin(x^x) – krok po kroku, proszę !

Odpowiedz
Dominik
28 sierpnia 2014 at 12:51

Mam pytanie, ile wynosi pochodna z \sqrt(2x-sinx(cos(x))^3)

Odpowiedz
Michał
4 lipca 2014 at 12:39

Mama pytanie, jak bedzie wygladala pochodna z arcsin(2x-1)? Czy po tym jak „trafi” pod pierwiastek to (2x-1)^2 nalezy rozwinac jak rownanie kwadratowe?

Odpowiedz
1. Krystian Karczyński
  4 lipca 2014 at 13:32
  
  Pójdzie tak:
  
  ${{\left( arcsin \left( 2x-1 \right) \right)}^{\prime }}=\frac{1}{\sqrt{1-{{\left( 2x-1 \right)}^{2}}}}{{\left( 2x-1 \right)}^{\prime }}=\frac{1}{\sqrt{1-\left( 4{{x}^{2}}-4x+1 \right)}}\cdot 2=$
  
  $=\frac{2}{\sqrt{1-4{{x}^{2}}+4x-1}}=\frac{2}{\sqrt{-4{{x}^{2}}+4x}}=\frac{2}{\sqrt{4\left( -{{x}^{2}}+x \right)}}=\frac{2}{\sqrt{4}\sqrt{x-{{x}^{2}}}}=$
  
  $=\frac{2}{2\sqrt{x-{{x}^{2}}}}=\frac{1}{\sqrt{x-{{x}^{2}}}}$
  
  Polecam: Kurs Pochodnych
Kasia Peczyńska
4 lipca 2014 at 01:10

Hej:)
Mam problem z policzeniem pochodnych II rzędu.
Przykład wygląda tak:
f(x,y)= 7- 4x/y – 2x^4y^3

Byłabym wdzięczna za pomoc:)
Pozdrawiam.

Odpowiedz
1. Krystian Karczyński
  15 lipca 2014 at 22:38
  
  Hej. To pójdzie tak:
  
  $f\left( x,y \right)=7-\frac{4x}{y}-2{{x}^{4}}{{y}^{3}}$
  
  Pochodne cząstkowe I-go rzędu:
  
  $\frac{\partial f}{\partial x}=\frac{\partial }{\partial x}\left( 7-\frac{4x}{y}-2{{x}^{4}}{{y}^{3}} \right)=\frac{\partial }{\partial x}\left( 7 \right)-\frac{\partial }{\partial x}\left( \frac{4x}{y} \right)-\frac{\partial }{\partial x}\left( 2{{x}^{4}}{{y}^{3}} \right)=0-\frac{4}{y}\frac{\partial }{\partial x}\left( x \right)-2{{y}^{3}}\frac{\partial }{\partial x}\left( {{x}^{4}} \right)=$
  
  $=0-\frac{4}{y}-2{{y}^{3}}\cdot 4{{x}^{3}}=-\frac{4}{y}-8{{y}^{3}}{{x}^{3}}$
  
  $\frac{\partial f}{\partial y}=\frac{\partial }{\partial y}\left( 7-\frac{4x}{y}-2{{x}^{4}}{{y}^{3}} \right)=\frac{\partial }{\partial y}\left( 7 \right)-\frac{\partial }{\partial y}\left( \frac{4x}{y} \right)-\frac{\partial }{\partial y}\left( 2{{x}^{4}}{{y}^{3}} \right)=0-4x\frac{\partial }{\partial x}\left( \frac{1}{y} \right)-2{{x}^{4}}\frac{\partial }{\partial y}\left( {{y}^{3}} \right)=$
  
  $=-4x\left( -\frac{1}{{{y}^{2}}} \right)-2{{x}^{4}}\cdot 3{{y}^{2}}=\frac{4x}{{{y}^{2}}}-6{{x}^{4}}{{y}^{2}}$
  
  Pochodne cząstkowe II-go rzędu:
  
  $\frac{{{\partial }^{2}}f}{\partial {{x}^{2}}}=\frac{\partial }{\partial x}\left( -\frac{4}{y}-8{{y}^{3}}{{x}^{3}} \right)=\frac{\partial }{\partial x}\left( -\frac{4}{y} \right)-\frac{\partial }{\partial x}\left( 8{{y}^{3}}{{x}^{3}} \right)=0-8{{y}^{3}}\frac{\partial }{\partial x}\left( {{x}^{3}} \right)=-8{{y}^{3}}\cdot 3{{x}^{2}}=-24{{x}^{2}}{{y}^{3}}$
  
  $\frac{{{\partial }^{2}}f}{\partial y\partial x}=\frac{\partial }{\partial y}\left( -\frac{4}{y}-8{{y}^{3}}{{x}^{3}} \right)=\frac{\partial }{\partial y}\left( -\frac{4}{y} \right)-\frac{\partial }{\partial y}\left( 8{{y}^{3}}{{x}^{3}} \right)=-4\frac{\partial }{\partial y}\left( \frac{1}{y} \right)-8{{x}^{3}}\frac{\partial }{\partial y}\left( {{y}^{3}} \right)=\frac{4}{{{y}^{2}}}-24{{x}^{3}}{{y}^{2}}$
  
  $\frac{{{\partial }^{2}}f}{\partial x\partial y}=\frac{\partial }{\partial x}\left( \frac{4x}{{{y}^{2}}}-6{{x}^{4}}{{y}^{2}} \right)=\frac{\partial }{\partial x}\left( \frac{4x}{{{y}^{2}}} \right)-\frac{\partial }{\partial x}\left( 6{{x}^{4}}{{y}^{2}} \right)=\frac{4}{{{y}^{2}}}\frac{\partial }{\partial x}\left( x \right)-6{{y}^{2}}\frac{\partial }{\partial x}\left( {{x}^{4}} \right)=\frac{4}{{{y}^{2}}}-24{{x}^{3}}{{y}^{2}}$
  
  $\frac{{{\partial }^{2}}f}{\partial {{y}^{2}}}=\frac{\partial }{\partial y}\left( \frac{4x}{{{y}^{2}}}-6{{x}^{4}}{{y}^{2}} \right)=\frac{\partial }{\partial y}\left( \frac{4x}{{{y}^{2}}} \right)-\frac{\partial }{\partial y}\left( 6{{x}^{4}}{{y}^{2}} \right)=4x\frac{\partial }{\partial y}\left( {{y}^{-2}} \right)-6{{x}^{4}}\frac{\partial }{\partial y}\left( {{y}^{2}} \right)=-\frac{8x}{{{y}^{3}}}-12{{x}^{4}}y$
  
  Polecam także mój Kurs Video: Kurs Funkcje Wielu Zmiennych
Katarzyna
22 czerwca 2014 at 22:11

Mam takie zadanie i nie umię go rozwiązać prosze o pomoc Z góry dziękuję 🙂
Znaleźć:
∂z/∂y dla danej funkcji:
z=x^2 √((x+y)/(x-y))

Odpowiedz
Ania
2 czerwca 2014 at 20:41

mam pare zadan i nie wiem jak je rozwiazac

Odpowiedz
Jolanta Lokajczyk
19 maja 2014 at 22:15

Proszę o pomoc w obliczeniu pochodnej z funkcji f(x)=〖log〗_2^5 (x+x^3)/arctgx (tzn f(x)=log stopnia 2 w potędze 5 z ((x+x^3)/arctgx) ). Radzę sobie z takim zadaniem, gdy log nie jest w potędze. W tym przypadku nie mam pewności jak to ma być prawidłowo obliczone.

Odpowiedz
Klaudia
11 maja 2014 at 00:59

Panie Krystianie zwracam się z ogromną prośbą…:) Otóż chodzi mi o zbadanie funkcji(tzn.zb.wartości,gdzie funkcja rośnie,gdzie maleje) ,ekstrema,punkty stałe, maksima i minima:
a)f(x)=Ax/(1+x),A>=2
b)f(x)=2/3x+1/3A,A>=11

Odpowiedz
1. Krystian Karczyński
  3 czerwca 2014 at 09:49
  
  a) 'A’ traktować trzeba jak stałą. Stosuję zasady i umowy podane w moim Kursie: Kurs Pochodne na Akademii
  
  $fleft( x right)=frac{Ax}{1+x},quad Age 2$
  
  Najpierw dziedzina funkcji:
  
  ${{1}^{0}}quad Df:xin Rbackslash { -1 }$
  
  ${{2}^{0}}quad {f}'left( x right)=frac{{{left( Ax right)}^{prime }}left( 1+x right)-Ax{{left( 1+x right)}^{prime }}}{{{left( 1+x right)}^{2}}}=frac{Aleft( 1+x right)-Ax}{{{left( 1+x right)}^{2}}}=frac{A+Ax-Ax}{{{left( 1+x right)}^{2}}}=frac{A}{{{left( 1+x right)}^{2}}}$
  
  ${{3}^{0}}quad frac{A}{{{left( 1+x right)}^{2}}}=0quad /cdot {{left( 1+x right)}^{2}}$ – mogę wykonać to mnożenie, ponieważ ${{left( 1+x right)}^{2}}$ jest zawsze nieujemne
  
  $A=0$
  
  Ale stała A nie może być równa 0, ze względu na założenie na początku zadania $Age 2$ . Czyli równanie nie ma rozwiązań, czyli pochodna nie ma miejsc zerowych.
  
  ${{4}^{0}}$ Rysuję jej przybliżony wykres:
  
  i piszę odpowiedź:
  
  ${{5}^{0}}$ Odp. Funkcja jest rosnąca w całej swojej dziedzinie, tzn. $xin Rbackslash { -1 }$ .
  
  Nie osiąga żadnych ekstremów.
kamil
8 maja 2014 at 21:01

Witam, mam pytanie ile wynoszą pochodne cząstkowe pierwszego rzędu z x^lny.

Odpowiedz
zustek
24 kwietnia 2014 at 14:32

Co się stało z możliwością, zobaczenia krok po kroku jak jest wyliczana pochodna

Odpowiedz
jonsi
14 kwietnia 2014 at 20:41

Panie Krystianie, a ile wynosi pochodna z f(x)=ln(x+/(ax-1))?

Odpowiedz
Karcia20
9 kwietnia 2014 at 20:54

Wiatm
Mój problem polega na tym że kompletnie zapomniałam jak liczyło się pochodne, przykład podam napewno banalnie prosty, ale może uda mi się jakoś odświeżyć pamieć.
$cos^2$ (x) – $sinus^2$ (x) .
Z góry dziękuję za pomoc

Odpowiedz
Paweł
5 kwietnia 2014 at 16:28

Witam
Mam problem z obliczeniem całki x^3*e^(-2x^4). Jak sie do tego zabrac? Jak na razie ani przez podstawienie ani przez częsci nic nie wychodzi chocbym nie wiem jak kombinował. Bardzo proszę o pomoc. Chciałbym jeszcze zapytac jak narysowac wykres takiego „cuda”?

Odpowiedz
adam
24 marca 2014 at 16:18

czy przypadkiem współczynnik przy drugiej pochodnej nie powinien być (1/a)(1/a-1) ?

Odpowiedz
1. Krystian Karczyński
  24 marca 2014 at 17:30
  
  Jasne, że powinien, gamoń ze mnie. Poprawiłem, wielkie dzięki za korektę…
ola
23 marca 2014 at 16:39

nie ma pojęcia, jaki może być wzór na n-tą pochodną pierwiastka (dowolnego stopnia). Czy mogę liczyć na pomoc?

Odpowiedz
1. Krystian Karczyński
  24 marca 2014 at 10:04
  
  Policzę kilka „pierwszych” pochodnych i zauważę ogólny wzór, O.K.?
  
  \sqrt[a]{x}[/latex]
  
  {{\left( \sqrt[a]{x} \right)}^{\prime }}={{\left( {{x}^{\frac{1}{a}}} \right)}^{\prime }}=\frac{1}{a}{{x}^{\tfrac{1}{a}-1}}[/latex]
  
  {{\left( \sqrt[a]{x} \right)}^{\prime \prime }}={{\left( \frac{1}{a}{{x}^{\tfrac{1}{a}-1}} \right)}^{\prime }}=\frac{1}{a}{{\left( {{x}^{\tfrac{1}{a}-1}} \right)}^{\prime }}=\frac{1}{a}\left( \tfrac{1}{a}-1 \right){{x}^{\tfrac{1}{a}-2}}[/latex]
  
  {{\left( \sqrt[a]{x} \right)}^{\prime \prime \prime }}={{\left( \frac{1}{a}\left( \tfrac{1}{a}-1 \right){{x}^{\tfrac{1}{a}-2}} \right)}^{\prime }}=\frac{1}{a}\left( \tfrac{1}{a}-1 \right){{\left( {{x}^{\tfrac{1}{a}-2}} \right)}^{\prime }}=\frac{1}{a}\left( \tfrac{1}{a}-1 \right)\left( \tfrac{1}{a}-2 \right){{x}^{\tfrac{1}{a}-3}}[/latex]
  
  {{\left( \sqrt[a]{x} \right)}^{\left( 4 \right)}}={{\left( \frac{1}{a}\left( \tfrac{1}{a}-1 \right)\left( \tfrac{1}{a}-2 \right){{x}^{\tfrac{1}{a}-3}} \right)}^{\prime }}=\frac{1}{a}\left( \tfrac{1}{a}-1 \right)\left( \tfrac{1}{a}-2 \right){{\left( {{x}^{\tfrac{1}{a}-3}} \right)}^{\prime }}=\frac{1}{a}\left( \tfrac{1}{a}-1 \right)\left( \tfrac{1}{a}-2 \right)\left( \tfrac{1}{a}-3 \right){{x}^{\tfrac{1}{a}-4}}[/latex]
  
  I myślę, że jest już dosyć jasne, że pochodna dowolnego rzędu n z pierwiastka stopnia a równa jest:
  
  {{\left( \sqrt[a]{x} \right)}^{\left( n \right)}}=\frac{1}{a}\left( \tfrac{1}{a}-1 \right)\left( \tfrac{1}{a}-2 \right)\cdot \ldots \cdot \left( \tfrac{1}{a}-\left( n-1 \right) \right){{x}^{\tfrac{1}{a}-n}}=\frac{1}{a}\left( \tfrac{1}{a}-1 \right)\left( \tfrac{1}{a}-2 \right)\cdot \ldots \cdot \left( \tfrac{1}{a}-n+1 \right){{x}^{\tfrac{1}{a}-n}}[/latex]
2. ola
  24 marca 2014 at 11:48
  
  super, dzięki
3. Krystian Karczyński
  24 marca 2014 at 17:29
  
  Nie ma za co, zwłaszcza, że zrobiłem błąd przy liczeniu (już poprawiłem). Przepraszam!
Kamil
18 marca 2014 at 00:24

y(x)=2^ln|ax-1| oblicz y'(x)

Mogę prosić o pomoc w rozwiązaniu?

Odpowiedz
Karolina
16 marca 2014 at 16:13

mam problem z obliczeniem pochodnej ((e^x)((x^2)-2x))/(x^4)

Odpowiedz
Kasia
26 lutego 2014 at 04:12

jak obliczyć pochodną drugiego rzędu z x^(1/2)*lnx?

Odpowiedz
1. Krystian Karczyński
  27 lutego 2014 at 09:46
  
  Jeżeli dobrze zrozumiałem wyrażenie:
  
  $y=\sqrt{x}ln x$
  
  ${y}'={{\left( \sqrt{x}ln x \right)}^{\prime }}={{\left( \sqrt{x} \right)}^{\prime }}ln x+\sqrt{x}{{\left( ln x \right)}^{\prime }}=\frac{1}{2\sqrt{x}}ln x+\sqrt{x}\cdot \frac{1}{x}=$
  
  $=\frac{ln x}{2\sqrt{x}}+\frac{{{x}^{\tfrac{1}{2}}}}{{{x}^{1}}}=\frac{ln x}{2\sqrt{x}}+\frac{1}{{{x}^{\tfrac{1}{2}}}}=\frac{ln x}{2\sqrt{x}}+\frac{1}{\sqrt{x}}=\frac{ln x}{2\sqrt{x}}+\frac{2}{2\sqrt{x}}=\frac{2+ln x}{2\sqrt{x}}$
  
  ${y}''={{\left( \frac{2+ln x}{2\sqrt{x}} \right)}^{\prime }}=\frac{{{\left( 2+ln x \right)}^{\prime }}2\sqrt{x}-\left( 2+ln x \right){{\left( 2\sqrt{x} \right)}^{\prime }}}{{{\left( 2\sqrt{x} \right)}^{2}}}=\frac{\frac{1}{x}\cdot 2\sqrt{x}-\left( 2+ln x \right)2\cdot \frac{1}{2\sqrt{x}}}{{{\left( 2\sqrt{x} \right)}^{2}}}=$
  
  $=\frac{\frac{2{{x}^{\tfrac{1}{2}}}}{{{x}^{1}}}-\frac{2+ln x}{\sqrt{x}}}{4x}=\frac{\frac{2}{\sqrt{x}}-\frac{2+ln x}{\sqrt{x}}}{4x}=\frac{\frac{-ln x}{\sqrt{x}}}{4x}=\frac{-ln x}{\sqrt{x}}\cdot \frac{1}{4x}=\frac{-ln x}{4x\sqrt{x}}$
Hubert
19 lutego 2014 at 19:40

Witam, mam pewien problem z pochodną z definicji w której i w liczniku i w mianowniku jest x. a mianowicie wygląda to tak : 2x-5/x-2 w punkcie 5. Czy mógłby Pan zapisac mi tylko początek ?
Ogólnie mam tak:
1) ta pochodna do oblicznia w pukcie x0=3
2) i tę samą do oblicznia normlnie z definicji
Pozdrawiam

Odpowiedz
1. Krystian Karczyński
  20 lutego 2014 at 09:55
  
  Pokażę w punkcie ${{x}_{0}}=5$ , dobrze?
  
  Poleci to tak:
  
  ${f}'\left( 5 \right)=\underset{\Delta x\to 0}{\mathop{lim }}\frac{f\left( 5+\Delta x \right)-f\left( 5 \right)}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim }}\frac{\frac{2\left( 5+\Delta x \right)-5}{5+\Delta x-2}-\frac{2\cdot 5-5}{5-2}}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim }}\frac{\frac{10+2\Delta x-5}{3+\Delta x}-\frac{5}{3}}{\Delta x}=$
  
  $=\underset{\Delta x\to 0}{\mathop{lim }}\frac{\frac{5+2\Delta x}{3+\Delta x}-\frac{5}{3}}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim }}\frac{\frac{3\left( 5+2\Delta x \right)}{3\left( 3+\Delta x \right)}-\frac{5\left( 3+\Delta x \right)}{3\left( 3+\Delta x \right)}}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim }}\frac{\frac{15+6\Delta x-15-5\Delta x}{3\left( 3+\Delta x \right)}}{\Delta x}=$
  
  $=\underset{\Delta x\to 0}{\mathop{lim }}\frac{\frac{\Delta x}{3\left( 3+\Delta x \right)}}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim }}\frac{\Delta x}{3\left( 3+\Delta x \right)}\frac{1}{\Delta x}=\underset{\Delta x\to 0}{\mathop{lim }}\frac{1}{3\left( 3+\Delta x \right)}=\frac{1}{9}$
Agnieszka
18 lutego 2014 at 20:28

Pochodna jakaś kosmos – na kalkulatorze wychodzi ładny wynik, ale dochodzę do pewnego momentu i koniec :[
(1/x)*e^(2x^2)
Pomocy proszę!

Odpowiedz
1. Krystian Karczyński
  28 lutego 2014 at 08:57
  
  To poleci tak (metodami z mojego Kursu) :
  
  ${{\left( \frac{1}{x}{{e}^{2{{x}^{2}}}} \right)}^{\prime }}={{\left( \frac{1}{x} \right)}^{\prime }}{{e}^{2{{x}^{2}}}}+\frac{1}{x}{{\left( {{e}^{2{{x}^{2}}}} \right)}^{\prime }}=-\frac{1}{{{x}^{2}}}{{e}^{2{{x}^{2}}}}+\frac{1}{x}{{e}^{2{{x}^{2}}}}\cdot {{\left( 2{{x}^{2}} \right)}^{\prime }}=$
  
  $=-\frac{{{e}^{2{{x}^{2}}}}}{{{x}^{2}}}+\frac{{{e}^{2{{x}^{2}}}}}{x}\cdot 4x=-\frac{{{e}^{2{{x}^{2}}}}}{{{x}^{2}}}+4{{e}^{2{{x}^{2}}}}$
Grzegorz
13 lutego 2014 at 23:46

Jaka pochodna wyjdzie z y=(lnx)^ (1/x) ?

Odpowiedz
Cezary Lech
13 lutego 2014 at 22:40

Witam mam problem z obliczeniem długości łuku spirali i nie wiem zbytnio jak za to się zabrać. Wychodzę do pana z zapytaniem o pomoc 😀 Zadanie brzmi następująco 😀 20. Oblicz długość łuku spirali o równaniu r=ae^k(fi), gdzie a>0,k>0 oraz w przedziale 0<(fi)<2\pi. Załącz szkic tego łuku. Z góry dziękuje za pomoc 😀

Odpowiedz
Iga
8 lutego 2014 at 16:32

Witam Panie Krystianie,
mam okropny problem w postaci policzenia ekstrema lokalnego funkcji f(x,y)=(x^2-y^2)e^x
Nie wychodzi mi policzenie pochodnej po df/dx i df/dy 🙁
Proszę o pomoc! 🙂

Odpowiedz
1. Krystian Karczyński
  11 lutego 2014 at 10:10
  
  $\frac{\partial f}{\partial x}=\frac{\partial }{\partial x}\left( \left( {{x}^{2}}-{{y}^{2}} \right){{e}^{x}} \right)=\left[ \frac{\partial }{\partial x}\left( {{x}^{2}}-{{y}^{2}} \right) \right]{{e}^{x}}+\left( {{x}^{2}}-{{y}^{2}} \right)\frac{\partial }{\partial x}{{e}^{x}}=2x{{e}^{x}}+\left( {{x}^{2}}-{{y}^{2}} \right){{e}^{x}}={{e}^{x}}\left( 2x+{{x}^{2}}-{{y}^{2}} \right)$
  
  $\frac{\partial f}{\partial y}=\frac{\partial }{\partial y}\left( \left( {{x}^{2}}-{{y}^{2}} \right){{e}^{x}} \right)={{e}^{x}}\frac{\partial }{\partial y}\left( {{x}^{2}}-{{y}^{2}} \right)={{e}^{x}}\left( -2y \right)=-2y{{e}^{x}}$
Piotrek
7 lutego 2014 at 19:58

witam, potrzebne obliczenie pochodnej jak dla mnie strasznej.
f(x) = log2(3^x+x^1/3)*arcsinx/2

Odpowiedz
Natalia
4 lutego 2014 at 19:20

Witam. Czy mógłby mi pan pomóc wyznaczyć ekstrema lokalne i calke nieoznaczoną funkcji f(x)=xexp(x)? Mam wielki problem z „exp”..

Odpowiedz
1. Krystian Karczyński
  5 lutego 2014 at 10:12
  
  Witam. Te całe wielkie „exp” to po prostu funkcja $e$ do tego co tam jest w nawiasie, czyli ma tu Pani funkcję: $f\left( x \right)=x{{e}^{x}}$ .
Ania
4 lutego 2014 at 13:52

Witam 🙂 mam problem z taką dziedziną : arcsin√9-x^2 + 1/sinπx, to pod pierwiastkiem wiadomo, jeśli chodzi o arcsin po rozpatrzeniu dwóch przypadków wyszły mi wszystkie liczby rzeczywiste o ile się nie mylę i nie jestem pewna co z sinusem… będę bardzo wdzięczna za pomoc 🙂

Odpowiedz
Marcin
3 lutego 2014 at 03:03

Witam serdecznie :>

czy w Pańskich kursach znajdują się gdzieś rzeczy dotyczące różniczkowalności funkcji w danym punkcie i zadania z parametrem z tym związane ?

Z góry dziękuję za odpowiedź.

Pozdrawiam.

Odpowiedz
1. Krystian Karczyński
  3 lutego 2014 at 10:46
  
  Witam, w Kursach nie ma, ale jest coś o tym na tym Wykładzie na blogu:
  
  https://blog.etrapez.pl/pochodne/badanie-istnienia-pochodnej-funkcji/
Ola
2 lutego 2014 at 16:45

WItam 😀 Borykam się z przykładowym zadaniem z egzaminu, dotyczącego badania przbeiegu funkcji. Wygląda tak: sinx – sin^2x. Dziedzina = R. Pochodna to cosx – 2sinx cosx dziedzina pochodnej też rzeczywiste.. Problem mam z przyrównaniem do zera, nie wiem jakie bedą rozwiązania, proszę o pomoc!:)

Odpowiedz
Magda
31 stycznia 2014 at 17:04

Witam 🙂 nie mogę sobie dać rady z dwoma przykładami z równań różniczkowych i proszę o pomoc: 1. y’=2y*(x-2) 2. y”-(x^2+1)=2xy’
Będę wdzięczna za pomoc POZDRAWIAM Magda

Odpowiedz
Grzesiek
31 stycznia 2014 at 14:52

Witam .
Mam problem z granicą lim x->infinity (x-x^2 *ln(1+1/x))
Próbowałem ja na różne sposoby , wychodziło mi 2, lub 0 . Opowiedz w książce jak i na wolframie to 1/2
Pozdrawiam

Odpowiedz
1. Grzesiek
  1 lutego 2014 at 01:08
  
  Nieaktualne, rozwiązałem
witek
31 stycznia 2014 at 14:23

Witam, mam problem z pochodną
(1/x+linx)^1/2 /3x^4+x^3+1
proszę o pomoc

Odpowiedz
1. Ryhor Abramovich
  15 października 2016 at 12:49
  
  $y equals fraction numerator square root of \begin display style 1 over x end style plus ln x end root over denominator 3 x to the power of 4 plus x cubed plus 1 end fraction$
  
  Rozwiązanie:
  
  $open parentheses u over v close parentheses apostrophe equals fraction numerator u apostrophe times v minus u times v apostrophe over denominator v squared end fraction$
  
  $y apostrophe equals fraction numerator open parentheses square root of \begin display style 1 over x end style plus ln x end root close parentheses apostrophe times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses minus square root of \begin display style 1 over x end style plus ln x end root times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses apostrophe over denominator open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses squared end fraction equals$
  
  $equals fraction numerator \begin display style fraction numerator 1 over denominator 2 square root of \begin display style 1 over x end style plus ln x end root end fraction end style times open parentheses \begin display style 1 over x end style plus ln x close parentheses apostrophe times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses minus square root of \begin display style 1 over x end style plus ln x end root times open parentheses 12 x cubed plus 3 x squared plus 0 close parentheses over denominator open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses squared end fraction equals$
  
  $equals fraction numerator \begin display style fraction numerator 1 over denominator 2 square root of \begin display style 1 over x end style plus ln x end root end fraction end style times open parentheses negative \begin display style 1 over x squared end style plus \begin display style 1 over x end style close parentheses times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses minus open parentheses 12 x cubed plus 3 x squared close parentheses times square root of \begin display style 1 over x end style plus ln x end root over denominator open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses squared end fraction equals$
  
  $equals fraction numerator \begin display style fraction numerator 1 over denominator 2 square root of \begin display style 1 over x end style plus ln x end root end fraction end style times \begin display style fraction numerator negative 1 plus x over denominator x squared end fraction end style times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses minus open parentheses 12 x cubed plus 3 x squared close parentheses times square root of \begin display style 1 over x end style plus ln x end root over denominator open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses squared end fraction equals$
  
  $equals fraction numerator open parentheses x minus 1 close parentheses times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses minus 2 x squared times open parentheses 12 x cubed plus 3 x squared close parentheses times open parentheses \begin display style 1 over x end style plus ln x close parentheses over denominator 2 x squared times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses squared times square root of \begin display style 1 over x end style plus ln x end root end fraction equals$
  
  $equals fraction numerator 3 x to the power of 5 plus x to the power of 4 plus x minus 3 x to the power of 4 minus x cubed minus 1 minus 24 x to the power of 4 minus 6 x cubed minus open parentheses 24 x to the power of 5 plus 6 x to the power of 4 close parentheses times ln x over denominator 2 open parentheses x times open parentheses 3 x to the power of 4 plus x cubed plus 1 close parentheses close parentheses squared times square root of \begin display style 1 over x end style plus ln x end root end fraction equals$
  
  $equals fraction numerator 3 x to the power of 5 minus 26 x to the power of 4 minus 7 x cubed plus x minus 1 minus open parentheses 24 x to the power of 5 plus 6 x to the power of 4 close parentheses times ln x over denominator 2 times open parentheses 3 x to the power of 5 plus x to the power of 4 plus x close parentheses squared times square root of \begin display style 1 over x end style plus ln x end root end fraction$
Krystian
31 stycznia 2014 at 13:21

Dzień dobry.

Czy w Pańskich kursach znajdę coś takiego jak „ZASTOSOWANIE CAŁEK” ? Chodzi mi głównie o :
– Pole obszaru ograniczonego przez funkcje (krzywe, sinusoidy, parabole pionowe/poziome itd.)
– Długość łuku krzywej
– Objętość bryły/bryły obrotowej,
– Pole powierzchni bryły obrotowej.

Pozdrawiam.

Odpowiedz
1. Krystian Karczyński
  31 stycznia 2014 at 13:25
  
  Dzień dobry
  
  Tak. To jest w Kursie Całek Oznaczonych, Niewłaściwych i Zastosowań Całek. Zapraszam:
  
  https://etrapez.pl/wybor-kursu/kurs-calki-oznaczone-niewlasciwe-i-zastosowania-calek/
Tomek
31 stycznia 2014 at 12:48

WItam, mam problem z pochodną czastkową (x + y) ^y . Jaka będzie wartość pochodnej po x i po y? Bardzo prosze o pomoc

Odpowiedz
Agata
30 stycznia 2014 at 13:41

Witam. Czy mógłby mi Pan podpowiedzieć jak obliczyć pochodną wyrażenia: Lnx^Lnx ?

Odpowiedz
1. Krystian Karczyński
  31 stycznia 2014 at 10:31
  
  Witam. No cóż, tą samą metodą co każdą sytuację typu (funkcja)^(funkcji), czyli:
  
  ${{\left( {{\left( ln x \right)}^{ln x}} \right)}^{\prime }}={{\left( {{e}^{ln x\cdot ln \left( ln x \right)}} \right)}^{\prime }}={{e}^{ln x\cdot ln \left( ln x \right)}}{{\left( ln x\cdot ln \left( ln x \right) \right)}^{\prime }}=$
  
  $={{e}^{ln x\cdot ln \left( ln x \right)}}\left( {{\left( ln x \right)}^{\prime }}ln \left( ln x \right)+ln x{{\left( ln \left( ln x \right) \right)}^{\prime }} \right)={{e}^{ln x\cdot ln \left( ln x \right)}}\left( \frac{1}{x}\cdot ln \left( ln x \right)+ln x\frac{1}{ln x}{{\left( ln x \right)}^{\prime }} \right)=$
  
  $={{e}^{ln x\cdot ln \left( ln x \right)}}\left( \frac{ln \left( ln x \right)}{x}+\frac{1}{x} \right)={{\left( ln x \right)}^{ln x}}\left( \frac{ln \left( ln x \right)+1}{x} \right)=\frac{{{\left( ln x \right)}^{ln x}}\left( ln \left( ln x \right)+1 \right)}{x}$
2. Agata
  31 stycznia 2014 at 11:24
  
  Dziękuję za odpowiedź. Nieoceniona jest Pana pomoc w postaci kursów, podpowiedzi i zadań.
Marek
29 stycznia 2014 at 18:59

Mógłby Pan wytłumaczyć dlaczego pochodna z x(x-1)^3 wynosi (x-1)^2(4x-1)^3 a nie 3x^2+6x+3? Moje rozumowanie: pochodna=3(x-1)^2*1

Odpowiedz
1. Krystian Karczyński
  31 stycznia 2014 at 10:51
  
  Tutaj na początku trzeba skorzystać z wzoru na pochodną mnożenia. Polecam mój Kurs , tam powolutku tłumaczę od podstaw 🙂
Magda
28 stycznia 2014 at 21:09

Witam 🙂 nie mogę sobie dać rady z dwoma przykładami z równań różniczkowych i proszę o pomoc: 1. y’=2y*(x-2) 2. y”-(x^2+1)=2xy’
Będę wdzięczna za pomoc POZDRAWIAM Magda

Odpowiedz
Jakub
26 stycznia 2014 at 18:56

Witam, mam do obliczenia następującą pochodną

.

w przykładzie zamias „log” jest „ln” niewiem czy to coś zmienia, a już kompletnie nie wiem jak się za to zabrać :/ Z góry dziękuję za pomoc, szczególnie jeżeli ktoś mi to rozpisze. Pozdrawiam 🙂

Odpowiedz
Paweł
26 stycznia 2014 at 12:24

Witam.Mam do obliczenia kilka pochodnych, ogólnie wzory,rozkład mam obcykane co i jak się robi.Jednak problem zaczyna pojawiać się wtedy kiedy zamiast literki x pojawiają się t,v,z itp.Nie do końca wiem jak mam się zachować w takim przykładzie jak : lnsqrt(1+t)/(1-t). Kiedy mam te literki traktować jako stałe a kiedy jako zmienne?

Odpowiedz
monika
25 stycznia 2014 at 21:28

Witam Panie Krystianie ! mam problem z obliczeniem 1 i 2giej pochodnej z lnx/sqrt(x). 🙁 potrzebne mi to do punktow przegiecia i wypukłości.. wynik z kalkulatora mi nie pomaga, ani nawet kroki.. prosze o pomoc

Odpowiedz
Sylwia
24 stycznia 2014 at 11:49

Witam. mam do obliczenia pochodną arcctg(1/sqrt(x)) jest to funkcja złożona wiadomo , gdy wstawiłam do kalkulatora wychodzi na początku inny wynik http://www.wolframalpha.com/share/clip?f=d41d8cd98f00b204e9800998ecf8427ehf53quid60
ale gdy wciskam step by step solution to na końcu jest inny wynik (ten mi wyszedł) jak z tamtego przejść na ten wynik z linku ?

Odpowiedz
Ania
21 stycznia 2014 at 18:46

Witam,
czy mógłby mi ktoś powiedzieć ( i wytłumaczyć)
ile wynosi pochodna z f(x)=log 10x ?
Chyba nie umiem tego wpisać do kalkulatora pochodnych albo czegoś nie rozumiem.
Z góry dziękuje za pomoc

Odpowiedz
1. Krystian Karczyński
  22 stycznia 2014 at 10:09
  
  Pochodna z $log 10x$ to pochodna z logarytmu o podstawie $10$ , liczymy ją ze wzoru: ${{\left( {{log }_{a}}x \right)}^{\prime }}=\frac{1}{xln a}$ , czyli:
  
  ${{\left( log 10x \right)}^{\prime }}=\frac{1}{10xln 10}{{\left( 10x \right)}^{\prime }}=\frac{1}{10xln 10}\cdot 10=\frac{1}{xln 10}$
  
  Problem z kalkulatorem jest taki, że on czyta „po amerykańsku”, a tam $log$ oznaczana logarytm NATURALNY (a u nas $ln$ ).
  
  Trzeba więc kalkulatorowi „zapodać” odpowiednią podstawę, np. wpisując: log_10(x)
aga
21 stycznia 2014 at 13:22

mam pewien problem robię zadanie z fizyki i mam wzór ogólny: I=1/8md^2. Muszę obliczyc pochodną I/d oraz I/m czy może mo ktoś pomóc ????Proszę

Odpowiedz
1. Krystian Karczyński
  22 stycznia 2014 at 16:22
  
  To będzie tak:
  
  $l=\frac{1}{8}m{{d}^{2}}$
  
  $\frac{\partial l}{\partial d}=\frac{\partial }{\partial d}\left( \frac{1}{8}m{{d}^{2}} \right)=\frac{1}{8}m\frac{\partial }{\partial d}\left( {{d}^{2}} \right)=\frac{1}{8}m\cdot 2d=\frac{1}{4}dm$
  
  $\frac{\partial l}{\partial m}=\frac{\partial }{\partial m}\left( \frac{1}{8}m{{d}^{2}} \right)=\frac{1}{8}{{d}^{2}}\frac{\partial }{\partial d}\left( m \right)=\frac{1}{8}{{d}^{2}}$
Justyna
17 stycznia 2014 at 14:21

Witam, czy byłaby możliwość pomocy z taką pochodną, bo za nic nie mogę jej wyliczyć, próbowałam sto razy i wychodzą mi jakieś dziwne, do niczego nie podobne wyniki.

Pochodna:
U(q)=D(1-e^(-S(q-q_0)))^2

Z góry dziękuję za pomoc.

Odpowiedz
1. Krystian Karczyński
  17 stycznia 2014 at 17:00
  
  Niestety, nie bardzo rozumiem zapis. D i S to są jakieś funkcje? Wiadomo, jakie? ${{q}_{_{0}}}$ to stała?
2. Justyna
  17 stycznia 2014 at 18:17
  
  D,s,q0 to stałe. Przepraszam bardzo. Zapomniałam dopisać.
3. Krystian Karczyński
  18 stycznia 2014 at 15:21
  
  Ok. Czyli całość wygląda, jak rozumiem, tak:
  
  $U\left( q \right)=D{{\left( 1-{{e}^{-S\left( q-{{q}_{0}} \right)}} \right)}^{2}}$
  
  No to wystarczy teraz nie spanikować i spokojnie policzyć pochodną:
  
  ${U}'\left( q \right)=2D\left( 1-{{e}^{-S\left( q-{{q}_{0}} \right)}} \right){{\left( 1-{{e}^{-S\left( q-{{q}_{0}} \right)}} \right)}^{\prime }}=2D\left( 1-{{e}^{-S\left( q-{{q}_{0}} \right)}} \right)\left( -{{e}^{-S\left( q-{{q}_{0}} \right)}} \right){{\left( -S\left( q-{{q}_{0}} \right) \right)}^{\prime }}=$
  
  $=2D\left( 1-{{e}^{-S\left( q-{{q}_{0}} \right)}} \right)\left( -{{e}^{-S\left( q-{{q}_{0}} \right)}} \right)\left( -S \right){{\left( q-{{q}_{0}} \right)}^{\prime }}=2DS{{e}^{-S\left( q-{{q}_{0}} \right)}}\left( 1-{{e}^{-S\left( q-{{q}_{0}} \right)}} \right)$
4. Justyna
  22 stycznia 2014 at 22:13
  
  dziękuję bardzo.
Paula
13 stycznia 2014 at 21:22

Mógłby mi Pan pomóc w krotkim zadanku y=\sqrt((a+bx)/(a-bx)) y’=? tzn wynik wiem jaki wyjść powinien jednak przy obliczeniach wychodzi mi zupełnie co innego

Odpowiedz
1. Krystian Karczyński
  17 stycznia 2014 at 10:07
  
  Jasne:
  
  $y=\sqrt{\frac{a+bx}{a-bx}}$
  
  $={{\left( \sqrt{\frac{a+bx}{a-bx}} \right)}^{\prime }}=\frac{1}{2\sqrt{\frac{a+bx}{a-bx}}}{{\left( \frac{a+bx}{a-bx} \right)}^{\prime }}=\frac{1}{2\frac{\sqrt{a+bx}}{\sqrt{a-bx}}}\frac{{{\left( a+bx \right)}^{\prime }}\left( a-bx \right)-\left( a+bx \right){{\left( a-bx \right)}^{\prime }}}{{{\left( a-bx \right)}^{2}}}=$
  
  $=\frac{\sqrt{a-bx}}{2\sqrt{a+bx}}\frac{b\left( a-bx \right)-\left( a+bx \right)\left( -b \right)}{{{\left( a-bx \right)}^{2}}}=\frac{1}{2\sqrt{a+bx}}\frac{ba-{{b}^{2}}x+ba+{{b}^{2}}x}{{{\left( a-bx \right)}^{\frac{3}{2}}}}=\frac{1}{2\sqrt{a+bx}}\frac{2ba}{\sqrt{a-bx}\left( a-bx \right)}=$
  
  $=\frac{ba}{\sqrt{a+bx}\sqrt{a-bx}\left( a-bx \right)}=\frac{ba}{\sqrt{{{a}^{2}}-{{b}^{2}}{{x}^{2}}}\left( a-bx \right)}$
  
  Żeby wykombinować taką postać, jaka jest w WolframAlpha można polecieć tak:
  
  $y=\sqrt{\frac{a+bx}{a-bx}}$
  
  ${y}'={{\left( \sqrt{\frac{a+bx}{a-bx}} \right)}^{\prime }}=\frac{1}{2\sqrt{\frac{a+bx}{a-bx}}}{{\left( \frac{a+bx}{a-bx} \right)}^{\prime }}=\frac{1}{2\sqrt{\frac{a+bx}{a-bx}}}\frac{{{\left( a+bx \right)}^{\prime }}\left( a-bx \right)-\left( a+bx \right){{\left( a-bx \right)}^{\prime }}}{{{\left( a-bx \right)}^{2}}}=$
  
  $=\frac{1}{2\sqrt{\frac{a+bx}{a-bx}}}\frac{b\left( a-bx \right)-\left( a+bx \right)\left( -b \right)}{{{\left( a-bx \right)}^{2}}}=\frac{1}{2\sqrt{\frac{a+bx}{a-bx}}}\frac{ba-{{b}^{2}}x+ba+{{b}^{2}}x}{{{\left( a-bx \right)}^{2}}}=\frac{1}{2\sqrt{\frac{a+bx}{a-bx}}}\frac{2ba}{{{\left( a-bx \right)}^{2}}}=$
  
  $=\frac{ba}{{{\left( a-bx \right)}^{2}}\sqrt{\frac{a+bx}{a-bx}}}$
Łukasz
13 stycznia 2014 at 16:27

Przepraszam, co oznacza skrót „sec” i „csc”? przy obliczniu pochodnych z 1/cos^x i – 1/sin^x

Odpowiedz
1. Krystian Karczyński
  16 stycznia 2014 at 17:38
  
  Funkcja sec to tzw. „secans”. $sec x=\frac{1}{cos x}$
  
  Funkcja csc to tzw. „cosecans” $csc x=\frac{1}{sin x}$
Katarzyna
12 stycznia 2014 at 16:02

widzę, że niestety źle musiałam wpisać formułę, więc wpisuję pochodną jeszcze raz:
f(x)=cosx^sinx^3 (czyli cos x podniesiony do potęgi sinx^3)

Odpowiedz
1. Krystian Karczyński
  18 stycznia 2014 at 15:30
  
  Witam, zakładam, że chodzi o funkcję: $f\left( x \right)={{\left( cos x \right)}^{sin {{x}^{3}}}}$
  
  Jedziemy, sposobem z mojego Kursu Video:
  
  ${f}'\left( x \right)={{\left( {{\left( cos x \right)}^{sin {{x}^{3}}}} \right)}^{\prime }}={{\left( {{e}^{sin {{x}^{3}}ln cos x}} \right)}^{\prime }}={{e}^{sin {{x}^{3}}ln cos x}}{{\left( sin {{x}^{3}}ln cos x \right)}^{\prime }}=$
  
  $={{e}^{sin {{x}^{3}}ln cos x}}\left( {{\left( sin {{x}^{3}} \right)}^{\prime }}ln cos x+sin {{x}^{3}}{{\left( ln cos x \right)}^{\prime }} \right)={{e}^{sin {{x}^{3}}ln cos x}}\left( cos {{x}^{3}}\cdot {{\left( {{x}^{3}} \right)}^{\prime }}ln cos x+sin {{x}^{3}}\frac{1}{cos x}{{\left( cos x \right)}^{\prime }} \right)=$
  
  $={{e}^{sin {{x}^{3}}ln cos x}}\left( 3{{x}^{2}}cos {{x}^{3}}ln cos x+sin {{x}^{3}}\frac{1}{cos x}\left( -sin x \right) \right)={{e}^{sin {{x}^{3}}ln cos x}}\left( 3{{x}^{2}}cos {{x}^{3}}ln cos x-tgxsin {{x}^{3}} \right)$
  
  Z pochodną drugiego rzędu już wymiękłem, przepraszam, p. Katarzyno.
2. Katarzyna
  22 stycznia 2014 at 07:38
  
  Dziękuję za odpowiedź. Nie spodziewałam się, że to jest aż TAKIE trudne, szczególnie, że nie jestem na studiach matematycznych. Bardzo mi Pan pomógł.
  Pozdrawiam, Katarzyna
Katarzyna
12 stycznia 2014 at 16:00

Witam, mam problem z pochodną: f(x)=cos x^sin x^3[/latex][/latex]. Muszę obliczyć pochodne 1 i 2 stopnia.
Proszę o pomoc

Odpowiedz
Paulina
10 stycznia 2014 at 14:37

Witam, mam taki problem próbuję wyliczyć pochodną z y=x^2*2^x*sinx, kompletnie nie wiem jak się do tego zabrać. Bardzo proszę o pomoc.

Odpowiedz
Ada
9 stycznia 2014 at 18:32

Potrzebuje pomocy obliczyć drugą pochodną funkcji: f(x)=e^3x^2+2x, wszystko po „e” jest w jej potędze.?

Odpowiedz
1. Michał
  18 stycznia 2014 at 16:26
  
  jeżeli chodzi Ci o pochodną z czegoś takiego [e^(3x)]^(2+2x) to po prostu mnożysz wykładniki i masz e^[3x*(2+2x)] a z tego to już nie problem pochodną wziąć 😉
2. Krystian Karczyński
  21 stycznia 2014 at 10:18
  
  Jeżeli miało być tak:
  
  $f\left( x \right)={{e}^{3{{x}^{2}}+2x}}$
  
  to będzie tak:
  
  ${f}'\left( x \right)={{\left( {{e}^{3{{x}^{2}}+2x}} \right)}^{\prime }}={{e}^{3{{x}^{2}}+2x}}{{\left( 3{{x}^{2}}+2x \right)}^{\prime }}={{e}^{3{{x}^{2}}+2x}}\left( 6x+2 \right)$
  
  ${f}''\left( x \right)={{\left( {{e}^{3{{x}^{2}}+2x}}\left( 6x+2 \right) \right)}^{\prime }}={{\left( {{e}^{3{{x}^{2}}+2x}} \right)}^{\prime }}\left( 6x+2 \right)+{{e}^{3{{x}^{2}}+2x}}{{\left( 6x+2 \right)}^{\prime }}=$
  
  $={{e}^{3{{x}^{2}}+2x}}{{\left( 3{{x}^{2}}+2x \right)}^{\prime }}\left( 6x+2 \right)+{{e}^{3{{x}^{2}}+2x}}{{\left( 6x+2 \right)}^{\prime }}={{e}^{3{{x}^{2}}+2x}}{{\left( 6x+2 \right)}^{2}}+6{{e}^{3{{x}^{2}}+2x}}=$
  
  $={{e}^{3{{x}^{2}}+2x}}\left[ {{\left( 6x+2 \right)}^{2}}+6 \right]={{e}^{3{{x}^{2}}+2x}}\left( 36{{x}^{2}}+24x+4+6 \right)={{e}^{3{{x}^{2}}+2x}}\left( 36{{x}^{2}}+24x+10 \right)$
kacper
7 stycznia 2014 at 00:58

(sin(2x-1))’
dlaczego w wyniku jest 2cos(1-2x), a nie 2cos(2x-1)??

Odpowiedz
1. Krystian Karczyński
  7 stycznia 2014 at 10:15
  
  To ten sam wynik.
  
  Cosinus jest funkcją parzystą, czyli $cos x=cos \left( -x \right)$ .
  
  Czyli: $cos \left( 2x-1 \right)=cos \left[ -\left( 2x-1 \right) \right]=cos \left( -2x+1 \right)=cos \left( 1-2x \right)$
  
  Niestety, taki wątpliwy „urok” kalkulatorów, że czasami przedstawiają wynik nie w tej postaci, w której nam wychodzi z „naszych” algorytmów liczenia.
2. kacper
  31 stycznia 2014 at 01:19
  
  Dzięki !!
  Jakie to proste 😀
Ania
4 stycznia 2014 at 13:55

Dzień dobry. Mam do obliczenia takie pochodne sin^2*3x oraz cos^2*3x. W książce odpowiedź do pierwszej funkcji 6sin6x, a do drugiej -6sin6x, kiedy mnie cały czas uparcie wychodzi 6sin3xcos3x oraz 6cos3xsin3x. Nie mam pojęcia co dzieję się w obu przypadkach z cosinusem,jaki wzór tu zastosowano… Bardzo proszę o pomoc!

Odpowiedz
Krystian
3 stycznia 2014 at 01:58

Mam pytanie , dla mnie dosyć ważne x^2*2^x*sinx jak obliczyć z tego pochodną , aby wyszło coś takiego y'(x) = 2^x x (x cos(x)+(x log(2)+2) sin(x)) . Nie mam pojęcia z jakiego wzoru pan to obliczył , gdyż w kursie w drugiej lekcji nie było żadnego przykładu z pochodną z trzema czynnikami pomnożone przez siebie , próbowałem ze wzoru na mnożenie ale mi nie wyszło PROSZĘ O POMOC

Odpowiedz
1. Damian M
  6 stycznia 2014 at 01:20
  
  Ziom, wzór na pochodna 3 czynnikow wydlada tak, mniej wiecej. fx-1czynnik, gx-2czynnik, tx-3czynnik
  a więc masz y’= fx’*gx*tx + fx*gx’*tx + fx*gx*tx’
Dominika
17 grudnia 2013 at 13:08

Witam, mam prośbę, męcze się z zadaniem już pare dni i nie moge rozwiązać, mogę liczyć na pomoc?
Obliczyć pochodną:
(a/b)^x * (b/x)^a * (x/a)^b , gdzie a,b>0

Odpowiedz
Magda
6 grudnia 2013 at 16:02

witam, mam problem z obliczeniem pochodnych arcsin^9 4x i log3(cosx) . Moge liczyc na pomoc?

Odpowiedz
Dominika
2 grudnia 2013 at 22:38

Witam Mam mały problem z matematyką .
Mianowicie dostałam zadanie na pierwszym roku studiów i mam z nim ogromny kłopot.
Lim=(1/x-1/sinx) oczywiscie x dąży do zera. Czy mogę liczyć na szczegółowe rozwiązanie z wytłumaczeniem krok po kroku ?

Odpowiedz
Piotrek
24 listopada 2013 at 03:35

Witam Panie krystianie czy mógłbym liczyć na pomoc w zadaniach nr 36,37 z kursu pochodnych ? mianowicie chodzi mi o przykład
(lnx)^x oraz (1+x)^sinx . Z góry Dziękuje i Pozdrawiam

Odpowiedz
1. Ryhor Abramovich
  15 października 2016 at 12:18
  
  Pierwszy przykład rozwiązany został tutaj:
  
  https://blog.etrapez.pl/pochodne/kalkulator-do-pochodnych/#comment-59660
  
  Drugi liczymy w sposób analogiczny:
  
  $y equals open parentheses 1 plus x close parentheses to the power of sin x end exponent equals e to the power of ln open parentheses 1 plus x close parentheses to the power of sin x end exponent end exponent equals e to the power of sin x times ln open parentheses 1 plus x close parentheses end exponent$
  
  $y apostrophe equals e to the power of sin x times ln open parentheses 1 plus x close parentheses end exponent times open parentheses sin x times ln open parentheses 1 plus x close parentheses close parentheses apostrophe equals e to the power of sin x times ln open parentheses 1 plus x close parentheses end exponent times open parentheses open parentheses sin x close parentheses apostrophe times ln open parentheses 1 plus x close parentheses plus sin x times open parentheses ln open parentheses 1 plus x close parentheses close parentheses apostrophe close parentheses equals$
  
  $e to the power of ln open parentheses 1 plus x close parentheses to the power of sin x end exponent end exponent times open parentheses cos x times ln open parentheses 1 plus x close parentheses plus sin x times fraction numerator 1 over denominator 1 plus x end fraction times open parentheses 1 plus x close parentheses apostrophe close parentheses equals$
  
  $equals open parentheses 1 plus x close parentheses to the power of sin x end exponent times open parentheses cos x times ln open parentheses 1 plus x close parentheses plus fraction numerator sin x over denominator 1 plus x end fraction times open parentheses 0 plus 1 close parentheses close parentheses equals$
  
  $open parentheses 1 plus x close parentheses to the power of sin x end exponent times open parentheses cos x times ln open parentheses 1 plus x close parentheses plus fraction numerator sin x over denominator 1 plus x end fraction close parentheses$
Kamil
21 listopada 2013 at 12:20

Witam
mam wzór g=4pi^2*n^2(l+d/2)/t^2 mam niepewność pomiaru oszacować metodą rożniczkowania wzoru, delta g=|dg/dt|* delta t + |dg/dd| * delta d+ |dg/dl|* delta l = ?
mam wzór dg/dt=-8pi^2n^2(l+d/2)/t^3. a jak policzyc |dg/dd| i |dg/dl| czy mógłby mi ktoś pomóc ?

Odpowiedz
konrad
8 listopada 2013 at 12:48

Mam wielki problem z przykładem z mojego kolokwium, mianowicie: Zbadać monotoniczność i wyznaczyć ekstrema lokalne funkcji: y= 2x/x^2+1, oraz funkcji y= x*sqrt(4 – x^2). W pierwszej funkcji znak „/” zastępuje kreskę ułamkową. Bardzo proszę o pomoc z tymi przykładami. Będę bardzo wdzięczny.

Odpowiedz
Łukasz
8 listopada 2013 at 00:10

hmm to teraz wszystko jasne, nie wiedziałem, że ln10 to stała. Dziękuje za rozwiązanie.

Odpowiedz
Łukasz
6 listopada 2013 at 01:22

Witam, nie mogę rozwiązać przykładu 7 z Twierdzenia de L’Hospitala, a mianowicie: lim x->nieskończoność x^3/10^x.
W mianowniku wychodzi mi jakieś 10^x razy ln10 z wzoru na pochodną a^x. Kolejna pochodna z tego to jakieś cuda na kiju :D.

Odpowiedz
1. Krystian Karczyński
  7 listopada 2013 at 10:35
  
  Eeeeee tam, jakie cuda na kiju, prościutka pochodna. $ln10$ to jest zwykła stała, taka sama jak $2$ , albo $15$ .
  
  Robi się tak:
  
  $\underset{x\to \infty }{\mathop{lim }}\frac{{{x}^{3}}}{{{10}^{x}}}\underset{H}{\overset{\left[ \tfrac{\infty }{\infty } \right]}{\mathop{=}}}\underset{x\to \infty }{\mathop{lim }}\frac{3{{x}^{2}}}{{{10}^{x}}ln 10}\underset{H}{\overset{\left[ \tfrac{\infty }{\infty } \right]}{\mathop{=}}}\underset{x\to \infty }{\mathop{lim }}\frac{{{\left( 3{{x}^{2}} \right)}^{\prime }}}{{{\left( {{10}^{x}}ln 10 \right)}^{\prime }}}=\underset{x\to \infty }{\mathop{lim }}\frac{3{{\left( {{x}^{2}} \right)}^{\prime }}}{ln 10{{\left( {{10}^{x}} \right)}^{\prime }}}=\underset{x\to \infty }{\mathop{lim }}\frac{6x}{{{10}^{x}}{{\left( ln 10 \right)}^{2}}}\underset{H}{\overset{\left[ \tfrac{\infty }{\infty } \right]}{\mathop{=}}}\underset{x\to \infty }{\mathop{lim }}\frac{6}{{{10}^{x}}{{\left( ln 10 \right)}^{3}}}=0$
michał
5 listopada 2013 at 19:06

Panie Krystianie, skorzystałem z Pana kalkulatora dla przykładu pochodnej y=ln(x+\sqrt(x^2+1)) i otrzymałem prawidłowy wynik (skonfron\towałem go z odpowiedzią w mojej książce do analizy matematycznej). Z przykładem tym męczę się już jakiś czas i nie wiem jak dojść do końcowego, najbardziej uproszczonego wyniku wyniku. Bardzo proszę o pomoc i pozdrawiam serdecznie, ten kalkulator to wspaniała sprawa : )

Odpowiedz
1. Krystian Karczyński
  8 listopada 2013 at 09:56
  
  Jasne, już pokazuję krok po kroku:
  
  $y=ln \left( x+\sqrt{{{x}^{2}}+1} \right)$
  ${y}'={{\left( ln \left( x+\sqrt{{{x}^{2}}+1} \right) \right)}^{\prime }}=\frac{1}{x+\sqrt{{{x}^{2}}+1}}{{\left( x+\sqrt{{{x}^{2}}+1} \right)}^{\prime }}=\frac{1}{x+\sqrt{{{x}^{2}}+1}}\left( {{\left( x \right)}^{\prime }}+{{\left( \sqrt{{{x}^{2}}+1} \right)}^{\prime }} \right)=$
  $=\frac{1}{x+\sqrt{{{x}^{2}}+1}}\left( {{\left( x \right)}^{\prime }}+{{\left( \sqrt{{{x}^{2}}+1} \right)}^{\prime }} \right)=\frac{1}{x+\sqrt{{{x}^{2}}+1}}\left( 1+\frac{1}{2\sqrt{{{x}^{2}}+1}}{{\left( {{x}^{2}}+1 \right)}^{\prime }} \right)=$
  $=\frac{1}{x+\sqrt{{{x}^{2}}+1}}\left( 1+\frac{1}{2\sqrt{{{x}^{2}}+1}}\cdot 2x \right)=\frac{1}{x+\sqrt{{{x}^{2}}+1}}\left( 1+\frac{x}{\sqrt{{{x}^{2}}+1}} \right)=\frac{1}{x+\sqrt{{{x}^{2}}+1}}+\frac{x}{\left( x+\sqrt{{{x}^{2}}+1} \right)\sqrt{{{x}^{2}}+1}}=$
  $=\frac{\sqrt{{{x}^{2}}+1}}{\left( x+\sqrt{{{x}^{2}}+1} \right)\sqrt{{{x}^{2}}+1}}+\frac{x}{\left( x+\sqrt{{{x}^{2}}+1} \right)\sqrt{{{x}^{2}}+1}}=\frac{x+\sqrt{{{x}^{2}}+1}}{\left( x+\sqrt{{{x}^{2}}+1} \right)\sqrt{{{x}^{2}}+1}}=\frac{1}{\sqrt{{{x}^{2}}+1}}$
2. michał
  8 listopada 2013 at 12:39
  
  Serdecznie dziękuję Panu za pomoc. Pozdrawiam.
anna
4 listopada 2013 at 14:19

czy mogłby ktoś napisać ile wynosi pochodan po x1 i po x2 ze wzroru (x1 do potęgi 1/3 + x2 do potęgi 1/3 )^3

Odpowiedz
1. Krystian Karczyński
  5 listopada 2013 at 10:19
  
  \frac{\partial }{\partial {{x}_{1}}}\left( {{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{3}} \right)=3{{\left( {{\left( {{x}_{1}} \right)}^{\tfrac{1}{3}}}+{{\left( {{x}_{2}} \right)}^{\tfrac{1}{3}}} \right)}^{2}}\cdot \frac{\partial }{\partial {{x}_{1}}}\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)=3{{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{2}}\cdot \frac{1}{3}{{x}_{1}}^{\tfrac{2}{3}}=\sqrt[3]{{{x}_{1}}^{2}}{{\left( \sqrt[3]{{{x}_{1}}}+\sqrt[3]{{{x}_{2}}} \right)}^{2}}[/latex]
  
  \frac{\partial }{\partial {{x}_{2}}}\left( {{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{3}} \right)=3{{\left( {{\left( {{x}_{1}} \right)}^{\tfrac{1}{3}}}+{{\left( {{x}_{2}} \right)}^{\tfrac{1}{3}}} \right)}^{2}}\cdot \frac{\partial }{\partial {{x}_{2}}}\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)=3{{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{2}}\cdot \frac{1}{3}{{x}_{2}}^{\tfrac{2}{3}}=\sqrt[3]{{{x}_{2}}^{2}}{{\left( \sqrt[3]{{{x}_{1}}}+\sqrt[3]{{{x}_{2}}} \right)}^{2}}[/latex]
2. anna
  5 listopada 2013 at 11:18
  
  Dziękuję bardzo za odpowiedż, z tym, że nie rozumiem dlaczego pochodna po x1 (x1 do potegi 1/3+x2 do potęgi1/3 ) to jest 1/3x1do potęgi2/3 a nie do potęgi (-2/3 )? wydawało mi się że wzór to alfa x alfa-1
3. anna
  5 listopada 2013 at 11:22
  
  i jeszcze mam pytanie (K+L)do potęgi 1/2 to pochodna po K to 1/2(K+L)do potęgi(-1*/2)*1?
  a pochodna po L to 1/2 (K+L)do potęgi(-1/2)*1?
4. Krystian Karczyński
  6 listopada 2013 at 10:35
  
  Bo mi się pomyliło… Powinno być oczywiście (tak jak Pani pisze):
  
  \frac{\partial }{\partial {{x}_{1}}}\left( {{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{3}} \right)=3{{\left( {{\left( {{x}_{1}} \right)}^{\tfrac{1}{3}}}+{{\left( {{x}_{2}} \right)}^{\tfrac{1}{3}}} \right)}^{2}}\cdot \frac{\partial }{\partial {{x}_{1}}}\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)=3{{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{2}}\cdot \frac{1}{3}{{x}_{1}}^{-\tfrac{2}{3}}=\frac{1}{\sqrt[3]{{{x}_{1}}^{2}}}{{\left( \sqrt[3]{{{x}_{1}}}+\sqrt[3]{{{x}_{2}}} \right)}^{2}}=\frac{{{\left( \sqrt[3]{{{x}_{1}}}+\sqrt[3]{{{x}_{2}}} \right)}^{2}}}{\sqrt[3]{{{x}_{1}}^{2}}}[/latex]
  
  \frac{\partial }{\partial {{x}_{2}}}\left( {{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{3}} \right)=3{{\left( {{\left( {{x}_{1}} \right)}^{\tfrac{1}{3}}}+{{\left( {{x}_{2}} \right)}^{\tfrac{1}{3}}} \right)}^{2}}\cdot \frac{\partial }{\partial {{x}_{2}}}\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)=3{{\left( {{x}_{1}}^{\tfrac{1}{3}}+{{x}_{2}}^{\tfrac{1}{3}} \right)}^{2}}\cdot \frac{1}{3}{{x}_{1}}^{-\tfrac{2}{3}}=\frac{1}{\sqrt[3]{{{x}_{2}}^{2}}}{{\left( \sqrt[3]{{{x}_{1}}}+\sqrt[3]{{{x}_{2}}} \right)}^{2}}=\frac{{{\left( \sqrt[3]{{{x}_{1}}}+\sqrt[3]{{{x}_{2}}} \right)}^{2}}}{\sqrt[3]{{{x}_{2}}^{2}}}[/latex]
aldan5
31 października 2013 at 15:48

Witam,
Trochę poza tematem, ale może ktoś pomoże w rozwiązaniu zadań:
Witam, czy ktoś mógłby pomóc w rozwiązaniu kilku zadań? Obliczyć pole figury ograniczonej krzywymi:
a) x+27y=27, y=0, x=-3, x=2
b) y=x/27, y=0, x=-2, x=-1
wystarczy podać co ma być pod całką, dalej już łatwo pójdzie.
a także:
wierzchołki figury są w punktach:
A1 (27; 3;6); A2( 2; 27; 1) ; A3(-27;0; 1) i A4(-4; 6;-27).
znaleźć:
1. długość krawędzi A1A2
2. kąt między krawędziami A1A1 i A1A3
3. równanie krawędzi A1A4
4. równanie ściany A1,A2,A3
5. kąt pomiędzy krawędzią A1A4 a ścianą A1,A2
6. pole ściany A1,A2,A3
7. pojemność figury
Jeżeli ktoś ma jakiś podobny przykład rozwiązany może być, najważniejsze mi poznać zasadę rozwiązania takiego typu zadania…
Będę bardzo bardzo wdzięczna za pomoc.

Odpowiedz
aldan5
23 października 2013 at 12:16

i jeszcze jedno pytanko:
z=lnx+cos27y-(27x/27y) czy pochodna z’=(1/x)-(1/y)? 🙂

Odpowiedz
1. Krystian Karczyński
  25 października 2013 at 11:00
  
  Nie. To jest funkcja dwóch zmiennych (x i y). Będzie miała zatem dwie pochodne cząstkowe:
  
  $\frac{\partial z}{\partial x}=\frac{1}{x}-\frac{1}{y}$
  
  $\frac{\partial z}{\partial y}=-27sin \left( 27y \right)+\frac{x}{{{y}^{2}}}$
Natalia
23 października 2013 at 10:52

Czy ktoś może mi podpowiedzieć jaka będzie pochodna po x1 z lnx1+x2 oraz pochodna po x2 z tej samej funkcji?

Odpowiedz
aldan5
22 października 2013 at 21:56

jak policzyć pochodną układu? y= {x=ln(27+t^2), y=2sin^28t

Odpowiedz
1. Krystian Karczyński
  23 października 2013 at 09:28
  
  To nie jest układ, to jest JEDNA funkcja dana w postaci parametrycznej 🙂
  
  W kalkulatorze na tej stronie się nie da, ale można użyć tego:
  
  Kalkulator do pochodnych funkcji parametrycznych
2. aldan5
  23 października 2013 at 09:37
  
  dzięki za pomoc 🙂
Natalia
21 października 2013 at 12:46

jak w tym programie policzyć pochodną po x1 z lnx1+x2 oraz pochodna po x2 z tej samej funkcji?

Odpowiedz
angelika
22 sierpnia 2013 at 08:13

Witam,

mam problem z pochodną cząstkową z/y:
z=x^2*pierwiastek z (x+y/x-y)

Bardzo proszę o pomoc,
pozdrawiam.

Odpowiedz
1. Krystian Karczyński
  22 sierpnia 2013 at 08:49
  
  Witam, bardzo proszę:
  
  $z={{x}^{2}}\sqrt{\frac{x+y}{x-y}}$
  
  $\frac{\partial z}{\partial y}=\frac{\partial }{\partial y}\left( {{x}^{2}}\sqrt{\frac{x+y}{x-y}} \right)={{x}^{2}}\frac{\partial }{\partial y}\left( \sqrt{\frac{x+y}{x-y}} \right)=$
  
  $={{x}^{2}}\frac{1}{2\sqrt{\tfrac{x+y}{x-y}}}\frac{\partial }{\partial y}\left( \frac{x+y}{x-y} \right)=$
  
  $={{x}^{2}}\frac{1}{2\tfrac{\sqrt{x+y}}{\sqrt{x-y}}}\frac{\tfrac{\partial }{\partial y}\left( x+y \right)\left( x-y \right)-\left( x+y \right)\tfrac{\partial }{\partial y}\left( x-y \right)}{{{\left( x-y \right)}^{2}}}=$
  
  $=\frac{{{x}^{2}}\sqrt{x-y}}{2\sqrt{x+y}}\frac{x-y+x+y}{{{\left( x-y \right)}^{2}}}=\frac{{{x}^{2}}\sqrt{x-y}}{2\sqrt{x+y}}\frac{2x}{{{\left( x-y \right)}^{2}}}=\frac{{{x}^{3}}\sqrt{x-y}}{\sqrt{x+y}{{\left( x-y \right)}^{2}}}$
  
  Jakby coś było niejasne, proszę dać znać 🙂
2. Mateusz
  5 września 2013 at 18:46
  
  Witam. Panie Krystianie od 2 dni nurtuje mnie pewien problem, który polega na pewnych pochodnych. Otóż mam problem z rozwiązanie pochodnych cząstkowych ( I i II rzędu ) oczywiście potrzebnych do obliczenia eksteremum funkcji. Oto funkcja :
  
  z = e ^ – x ( y ^ 2 – 2x ). Nie wychodzą mi pochodne cząstkowe. Drugi problem to : Oblicz ekstermum funkcji : z = x ^ 4 + y ^ 4 – 2 x ^ 2 – 2 y ^ 2 + 4xy. Dostalem takie zadanie na egzmainie i do dzisiaj nie mogę się z tym uporać.
  
  Bardzo proszę o pomoc. Pozdrawiam.
3. Krystian Karczyński
  11 września 2013 at 10:14
  
  Co do pierwszego przykładu, to trochę się rozmachnąłem i zrobiłem cały. Mam nadzieję, że dobrze odczytałem Pana zapis.
  
  Jak rozumiem, chodzi o funkcję: $z={{e}^{-x}}\left( {{y}^{2}}-2x \right)$
  
  Liczę:
  
  $\frac{\partial z}{\partial x}=\frac{\partial }{\partial x}\left( {{e}^{-x}}\left( {{y}^{2}}-2x \right) \right)=\frac{\partial }{\partial x}\left( {{e}^{-x}} \right)\left( {{y}^{2}}-2x \right)+{{e}^{-x}}\frac{\partial }{\partial x}\left( {{y}^{2}}-2x \right)=$
  
  $=-{{e}^{-x}}\left( {{y}^{2}}-2x \right)+{{e}^{-x}}\left( -2 \right)={{e}^{-x}}\left( -{{y}^{2}}+2x-2 \right)$
  
  $\frac{\partial z}{\partial y}=\frac{\partial }{\partial y}\left( {{e}^{-x}}\left( {{y}^{2}}-2x \right) \right)={{e}^{-x}}\frac{\partial }{\partial y}\left( {{y}^{2}}-2x \right)=2y{{e}^{-x}}$
  
  Teraz układ równań:
  
  $\{ \begin{matrix} & {{e}^{-x}}\left( -{{y}^{2}}+2x-2 \right)=0\quad /:{{e}^{-x}}\\ & 2y{{e}^{-x}}=0\quad /:{{e}^{-x}}\end{matrix}$
  
  $\{ \begin{matrix} & -{{y}^{2}}+2x-2=0 \\ & 2y=0\quad \Rightarrow \ y=0 \end{matrix}$
  
  Czyli biorąc pierwsze równanie:
  
  $-{{0}^{2}}+2x-2=0$
  
  $2x-2=0$
  
  $2x=2\quad /:1$
  
  $x=1$
  
  Mój punkt stacjonarny ma zatem współrzędne: ${{P}_{1}}\left( 1,0 \right)$
  
  Teraz druga część zadania:
  
  $\frac{{{\partial }^{2}}z}{\partial {{x}^{2}}}=\frac{\partial }{\partial x}\left[ {{e}^{-x}}\left( -{{y}^{2}}+2x-2 \right) \right]=$
  
  $=\frac{\partial }{\partial x}\left( {{e}^{-x}} \right)\left( -{{y}^{2}}+2x-2 \right)+{{e}^{-x}}\frac{\partial }{\partial x}\left( -{{y}^{2}}+2x-2 \right)=$
  
  $=-{{e}^{-x}}\left( -{{y}^{2}}+2x-2 \right)+{{e}^{-x}}\cdot 2={{e}^{-x}}\left( {{y}^{2}}-2x+4 \right)$
  
  $\frac{{{\partial }^{2}}z}{\partial y\partial x}=\frac{\partial }{\partial y}\left[ {{e}^{-x}}\left( -{{y}^{2}}+2x-2 \right) \right]={{e}^{-x}}\frac{\partial }{\partial y}\left( -{{y}^{2}}+2x-2 \right)=-2y{{e}^{-x}}$
  
  $\frac{{{\partial }^{2}}z}{\partial x\partial y}=\frac{\partial }{\partial x}\left( 2y{{e}^{-x}} \right)=2y\frac{\partial }{\partial x}\left( {{e}^{-x}} \right)=-2y{{e}^{-x}}$
  
  $\frac{{{\partial }^{2}}z}{\partial y\partial y}=\frac{\partial }{\partial y}\left( 2y{{e}^{-x}} \right)={{e}^{-x}}\frac{\partial }{\partial y}\left( 2y \right)=2{{e}^{-x}}$
  
  Tworzę z tych pochodnych cząstkowych drugiego rzędu odpowiedni wyznacznik:
  
  $W=\left| \begin{matrix} {{e}^{-x}}\left( {{y}^{2}}-2x+4 \right) & -2y{{e}^{-x}} \\ -2y{{e}^{-x}} & 2{{e}^{-x}} \end{matrix} \right|$
  
  Podstawiam do niego współrzędne punktu stacjonarnego:
  
  $W\left( {{P}_{1}} \right)=\left| \begin{matrix} {{e}^{-1}}\left( {{0}^{2}}-2\cdot 1+4 \right) & -2\cdot 0\cdot {{e}^{-1}} \\ -2\cdot 0\cdot {{e}^{-1}} & 2{{e}^{-1}} \end{matrix} \right|=\left| \begin{matrix} 2{{e}^{-1}} & 0 \\ 0 & 2{{e}^{-1}} \end{matrix} \right|={{\left( 2{{e}^{-1}} \right)}^{2}}$
  
  Wyznacznik jest większy od zera, a $\frac{{{\partial }^{2}}z}{\partial {{x}^{2}}}$ w tym punkcie także przyjmuje wartość większą od zera, zatem w punkcie ${{P}_{1}}\left( 1,0 \right)$ funkcja osiąga minimum.
  
  ${{z}_{min }}={{e}^{-1}}\left( {{0}^{2}}-2\cdot 1 \right)=-2{{e}^{-1}}=-2\cdot \frac{1}{e}=-\frac{2}{e}$
4. Mateusz
  12 września 2013 at 22:35
  
  Bardzo dziękuję panie Krystianie odpowiedż otrzymałem dzień przed egzamine poprawkowym co pomoglo rozwiązać jeden problem 🙂 Pozdrawiam serdecznie !!!
5. Krystian Karczyński
  13 września 2013 at 11:16
  
  No to dorzucę jeszcze ekstremum do tego drugiego przykładu i gratuluję (jak rozumiem) poprawkowego:
Iza
3 maja 2013 at 19:54

Dzień Dobry Panie Krystianie

Mam wielki problem z równaniem różniczkowym: y’ – 2xy = x
dochodzę do momentu obliczenia pochodnej i dalej ani rusz
Bardzo proszę Pana o pomoc

Pozdrawiam serdecznie

Odpowiedz
1. Iza
  15 maja 2013 at 21:06
  
  jest tu ktoś?
Marcin
11 kwietnia 2013 at 22:35

Dobry Wieczór Panie Krystianie!

Męczy mnie ostatnio dość pewnie prosta ale dla mnie nie typowa całka mianowicie:
http://www.wolframalpha.com/input/?i=Integral+%281%2F%28x\sqrtx%29%29dx+

Całka 1/x\sqrtx dx

Za pomocą jakiej metody można ten przykład rozwiązać?

Pozdrawiam serdecznie!

Odpowiedz
1. Krystian Karczyński
  19 kwietnia 2013 at 09:46
  
  Dzień dobry
  
  To rzeczywiście nietrudna całka:
  
  $\int{\frac{1}{x\sqrt{x}}dx}=\int{\frac{1}{x\cdot {{x}^{\tfrac{1}{2}}}}dx=}\int{\frac{1}{x\cdot {{x}^{\tfrac{1}{2}}}}dx}=\int{\frac{1}{{{x}^{\tfrac{3}{2}}}}dx}=\int{{{x}^{-\tfrac{3}{2}}}dx}=\frac{1}{-\tfrac{3}{2}+1}{{x}^{-\tfrac{3}{2}+1}}+C=$
  
  $=\frac{1}{-\tfrac{1}{2}}{{x}^{-\tfrac{1}{2}}}+C=-2\cdot \frac{1}{{{x}^{\tfrac{1}{2}}}}+C=-\frac{2}{\sqrt{x}}+C$
  
  Przykład w WolframAlpha
Ela
7 kwietnia 2013 at 22:25

Witam serdecznie Panie Krystianie!
Nie mogę sobie poradzić z przykładem z zakresu pochodnych cząstkowych

z = xlny – rozumiem że tu należy skorzystać ze wzoru na mnożenie pochodnych , lecz dalej stoję i nie wiem jak to ciachnąć
z= sin(xy)/x tak samo z tym

Prosiłabym o jakąś dobrą porade.
Pozdrawiam

Odpowiedz
1. Ela
  7 kwietnia 2013 at 23:19
  
  Poradziłam sobie z przykładem z=xlny 🙂
  więc jeszcze ten 2 🙂
2. Krystian Karczyński
  8 kwietnia 2013 at 13:03
  
  No to liczę 🙂
  
  Po zmiennej x:
  
  $\frac{\partial f}{\partial x}=\frac{\partial }{\partial x}\left( \frac{sin \left( xy \right)}{x} \right)=\frac{\tfrac{\partial }{\partial x}\left( sin \left( xy \right) \right)x-sin \left( xy \right)\tfrac{\partial }{\partial x}\left( x \right)}{{{x}^{2}}}=$
  
  $=\frac{cos \left( xy \right)\cdot \tfrac{\partial }{\partial x}\left( xy \right)\cdot x-sin \left( xy \right)\cdot 1}{{{x}^{2}}}=$
  
  $\frac{xycos \left( xy \right)-sin \left( xy \right)}{{{x}^{2}}}$
  
  Po zmiennej y:
  
  $\frac{\partial f}{\partial y}=\frac{\partial }{\partial y}\left( \frac{sin \left( xy \right)}{x} \right)=\frac{1}{x}\frac{\partial }{\partial y}\left( sin \left( xy \right) \right)=\frac{1}{x}cos \left( xy \right)\frac{\partial }{\partial y}\left( xy \right)=$
  
  $=\frac{1}{x}cos \left( xy \right)\cdot x=cos \left( xy \right)$
  
  Wynik możemy sprawdzić w WolframAlpha
  
  Wynik po zmiennej x
  
  Wynik po zmiennej y
3. Ela
  8 kwietnia 2013 at 15:27
  
  a paskudztwo takie jak z=yx^(2y)
  
  Dziękuje Panu bardzo ! Pochodne II rzędu wyszły bez żadnego problemu 😉
4. Ela
  8 kwietnia 2013 at 18:11
  
  po zmiennej y to jakas czarna magia
5. Krystian Karczyński
  9 kwietnia 2013 at 12:57
  
  Jedziemy:
  
  $z=y{{x}^{2y}}$
  
  $\frac{\partial z}{\partial x}=\frac{\partial }{\partial x}\left( y{{x}^{2y}} \right)=y\frac{\partial }{\partial x}\left( {{x}^{2y}} \right)=y\cdot 2y{{x}^{2y-1}}=2{{y}^{2}}{{x}^{2y-1}}$
  
  $\frac{\partial z}{\partial y}=\frac{\partial }{\partial y}\left( y{{x}^{2y}} \right)=\frac{\partial }{\partial y}\left( y \right){{x}^{2y}}+y\frac{\partial }{\partial y}\left( {{x}^{2y}} \right)={{x}^{2y}}+y{{x}^{2y}}ln x\cdot \frac{\partial }{\partial y}\left( 2y \right)=$
  
  $={{x}^{2y}}+2y{{x}^{2y}}ln x={{x}^{2y}}\left( 1+2yln x \right)$
  
  Wyniki można sprawdzić znowu w WolframAlpha:
  
  Wynik pochodnej po x
  
  Wynik pochodnej po y
Kasia
19 marca 2013 at 16:07

Błagam o pomoc!!
Nie mogę poradzić sobie z równaniem różniczkowym:

y’ = ( (x+1)/x )y = 3x ^2 e^ -x

Błagam o pomoc!!!!:(

Odpowiedz
1. Krystian Karczyński
  20 marca 2013 at 20:14
  
  O.K. ale albo jest jakiś błąd w formule, albo to są dwa równania, Pani Kasiu.
  
  Jedno z nich to:
  
  y’ = ( (x+1)/x )y
  
  a drugie:
  
  ( (x+1)/x )y = 3x ^2 e^ -x
  
  ?
Martyna
13 marca 2013 at 20:17

Panie Krystianie a jak wpisać w ten kalkulator pierwiastek piątego stopnia ?

Odpowiedz
1. Krystian Karczyński
  14 marca 2013 at 11:18
  
  Trzeba podnieść do potęgi $\frac{1}{5}$ , np: (sin(x))^(1/5)
Kornelia
27 lutego 2013 at 10:58

Mam pytanie dlaczego jak wpisuję y=pi + 3t nie wychodzi mi wynik… \pi jest jako stała? A z kolei jak wpisuję y= 4t to w ogóle nic nie wychodzi..
.. Pozdrawiam 😉

Odpowiedz
1. Krystian Karczyński
  12 marca 2013 at 14:26
  
  Kalkulator jest ustawiony na zmienną $x$ , a nie zmienną $t$ . Niech Pani wpisze y=pi+3x i y=4x, wszystko ładnie wyjdzie.
Miko
16 lutego 2013 at 20:53

Witam, mam pytanie, dlaczego przy liczeniu ekstremum po obliczeniu pochodnej z xlnx wynik jest równy logx+1 a x wychodzi wg odpowiedzi 1/e?

Odpowiedz
1. Miko
  16 lutego 2013 at 21:07
  
  to już wiem, tylko nie wiem teraz dlaczego zbiór f(maleje) (0,1) suma z (1,e) przy y=x/lnx tego to całkiem nie pojmuje
Kamil
12 lutego 2013 at 03:56

Witam, egzamin tuż tuż a mam problem z zadaniem takiego typu:

Wyprowadź z deﬁnicji wzór na pochodną funkcji f(x) = 2x^2 + 1.

Próbowałem rozwiązać to korzystając z Pańskich filmików lecz nie potrafię się za to zabrać.
Byłbym wdzięczny za odpowiedz.
Pozdrawiam.

Odpowiedz
1. Kamil
  12 lutego 2013 at 13:03
  
  Znam już odpowiedz do tego zadania, tak jak sądziłem była banalna.
  Pozdrawiam.
Adam
1 lutego 2013 at 00:57

Witam mam problem z taką pochodną:

x*a^x/a^x-1

liczyłem ją już kilka razy i za każdym razem wychodzi mi nieskaczonosc a powinno wyjść 1.

Prosze o pomoc.

Pozdrawiam 🙂

Odpowiedz
1. Ryhor Abramovich
  15 października 2016 at 11:52
  
  $y equals fraction numerator x times a to the power of x over denominator a to the power of x minus 1 end fraction$ , gdzie a – stała.
  
  Rozwiązanie:
  
  $open parentheses u over v close parentheses apostrophe equals fraction numerator u apostrophe times v minus u times v apostrophe over denominator v squared end fraction$ , a także $open parentheses u times v close parentheses apostrophe equals u apostrophe times v plus u times v apostrophe$
  
  $y apostrophe equals fraction numerator open parentheses x times a to the power of x close parentheses apostrophe times open parentheses a to the power of x minus 1 close parentheses minus open parentheses x times a to the power of x close parentheses times open parentheses a to the power of x minus 1 close parentheses apostrophe over denominator open parentheses a to the power of x minus 1 close parentheses squared end fraction equals$
  
  $equals fraction numerator open parentheses x apostrophe times a to the power of x plus x times open parentheses a to the power of x close parentheses apostrophe close parentheses times open parentheses a to the power of x minus 1 close parentheses minus open parentheses x times a to the power of x close parentheses times open parentheses a to the power of x times ln a minus 0 close parentheses over denominator open parentheses a to the power of x minus 1 close parentheses squared end fraction equals$
  
  $equals fraction numerator open parentheses 1 times a to the power of x plus x times a to the power of x times ln a close parentheses times open parentheses a to the power of x minus 1 close parentheses minus x times a to the power of x times a to the power of x times ln a over denominator open parentheses a to the power of x minus 1 close parentheses squared end fraction equals$
  
  $equals fraction numerator a to the power of 2 x end exponent minus a to the power of x plus x times a to the power of 2 x end exponent times ln a minus x times a to the power of x times ln a minus x times a to the power of 2 x end exponent times ln a over denominator open parentheses a to the power of x minus 1 close parentheses squared end fraction equals$
  
  $fraction numerator a to the power of 2 x end exponent minus a to the power of x minus x times a to the power of x times ln a over denominator open parentheses a to the power of x minus 1 close parentheses squared end fraction$
Kuba
30 stycznia 2013 at 21:14

Witam, mam problem z policzenie pochodnej y=(lnx)^x

Odpowiedz
Kuba
30 stycznia 2013 at 21:11

Zupełnie nie mam pojęcia jak rozwiazać pochodna y=(lnx)^x

Odpowiedz
1. Ryhor Abramovich
  15 października 2016 at 11:34
  
  $y equals open parentheses ln x close parentheses to the power of x$
  
  Rozwiązanie:
  
  Najpierw skorzystamy ze wzorów:
  
  $x equals e to the power of ln x end exponent$ , a także $ln x to the power of y equals y times ln x$ i zapisujemy funkcję w postaci:
  
  $y equals open parentheses ln x close parentheses to the power of x equals e to the power of ln open parentheses ln x close parentheses to the power of x end exponent equals e to the power of x times ln open parentheses ln x close parentheses end exponent$
  
  Dopiero teraz liczymy:
  
  $open parentheses e to the power of increment close parentheses apostrophe equals e to the power of increment times increment apostrophe$
  
  $open parentheses u times v close parentheses apostrophe equals u apostrophe times v plus u times v apostrophe$
  
  $y apostrophe equals open parentheses e to the power of x times ln open parentheses ln x close parentheses end exponent close parentheses apostrophe equals e to the power of x times ln open parentheses ln x close parentheses end exponent times open parentheses x times ln open parentheses ln x close parentheses close parentheses apostrophe equals e to the power of ln open parentheses ln x close parentheses to the power of x end exponent times open parentheses x apostrophe times ln open parentheses ln x close parentheses plus x times open parentheses ln open parentheses ln x close parentheses close parentheses apostrophe close parentheses equals$
  
  $equals open parentheses ln x close parentheses to the power of x times open parentheses 1 times ln open parentheses ln x close parentheses plus x times fraction numerator 1 over denominator ln x end fraction times open parentheses ln x close parentheses apostrophe close parentheses equals open parentheses ln x close parentheses to the power of x times open parentheses ln open parentheses ln x close parentheses plus x times fraction numerator 1 over denominator ln x end fraction times 1 over x close parentheses equals$
  
  $open parentheses ln x close parentheses to the power of x times open parentheses ln open parentheses ln x close parentheses plus fraction numerator 1 over denominator ln x end fraction close parentheses$
p
29 stycznia 2013 at 23:59

witam, proszę o pomoc jak odczytać z rysunku asymptoty i granice (jak je odróżnić). oraz bardzo proszę o jakiś materiał o obliczaniu granic funkcji. 🙂

Odpowiedz
Mateusz
28 stycznia 2013 at 19:09

Witam serdecznie, przerobiłem Pana kurs z geometrii analitycznej ciągi i pochodne…świetne przygotowanie do kolokwium.
Miałem tylko problem z jedną pochodną i proszę o rozwiązanie
y ’ = arcsin(x^2) / pierwiastek z 2 – tgx

Odpowiedz
1. Mateusz
  29 stycznia 2013 at 14:00
  
  pod pierwiastkiem tylko 2
  z gory dziekuje
2. Ryhor Abramovich
  14 października 2016 at 16:06
  
  $y equals fraction numerator a r c sin open parentheses x squared close parentheses over denominator square root of 2 minus t g x end fraction$
  
  Rozwiązanie:
  
  $open parentheses u over v close parentheses apostrophe equals fraction numerator u apostrophe times v minus u times v apostrophe over denominator v squared end fraction$
  
  $y apostrophe equals fraction numerator open parentheses a r c sin open parentheses x squared close parentheses close parentheses apostrophe times open parentheses square root of 2 minus t g x close parentheses minus a r c sin open parentheses x squared close parentheses times open parentheses square root of 2 minus t g x close parentheses apostrophe over denominator open parentheses square root of 2 minus t g x close parentheses squared end fraction equals$
  
  $equals fraction numerator \begin display style fraction numerator 1 over denominator square root of 1 minus open parentheses x squared close parentheses squared end root end fraction end style times open parentheses x squared close parentheses apostrophe times open parentheses square root of 2 minus t g x close parentheses minus a r c sin open parentheses x squared close parentheses times open parentheses 0 minus \begin display style fraction numerator 1 over denominator cos squared x end fraction end style close parentheses over denominator open parentheses square root of 2 minus t g x close parentheses squared end fraction equals$
  
  $equals fraction numerator \begin display style fraction numerator 1 over denominator square root of 1 minus x to the power of 4 end root end fraction end style times 2 x times open parentheses square root of 2 minus t g x close parentheses minus a r c sin open parentheses x squared close parentheses times open parentheses negative \begin display style fraction numerator 1 over denominator cos squared x end fraction end style close parentheses over denominator open parentheses square root of 2 minus t g x close parentheses squared end fraction equals$
  
  $equals fraction numerator \begin display style fraction numerator 2 x open parentheses square root of 2 minus t g x close parentheses over denominator square root of 1 minus x to the power of 4 end root end fraction end style plus \begin display style fraction numerator a r c sin open parentheses x squared close parentheses over denominator cos squared x end fraction end style over denominator open parentheses square root of 2 minus t g x close parentheses squared end fraction equals$ $equals fraction numerator 2 x times cos squared x times open parentheses square root of 2 minus t g x close parentheses plus square root of 1 minus x to the power of 4 end root times a r c sin open parentheses x squared close parentheses over denominator square root of 1 minus x to the power of 4 end root times open parentheses square root of 2 minus t g x close parentheses squared times cos squared x end fraction$
Piotr
28 stycznia 2013 at 11:50

Dzień dobry. Czy mógłby mi Pan pomóc z pochodną:

f(x) = 1/(2x) * ln(1+x^2) – arctgx

tam jest na początku ułamek razy logarytm naturalny.

Wynik przedstawić trzeba w najprostrzej postaci.

Odpowiedz
1. Awesome
  30 stycznia 2013 at 01:59
  
  Wrzucasz ln(…) na góre i zwykłe rozwiązanie na f(x)-g(x) na ln(,,,)/2x stosujesz f(x)/ g(x) wzor i masz… 😉
Karolina
27 stycznia 2013 at 18:17

WITAM przeszłam cały Pana kurs pochodny ale mam problem z jedną która występuje w Krysickim bardzo proszę o pomoc
y=4^xln4arctgx + 4^x/1+x^2

Odpowiedz
1. Krystian Karczyński
  28 stycznia 2013 at 10:44
  
  Witam,
  
  Niestety, mogłem źle zinterpretować, co jest przez co dzielone, co podniesione do czego i przemnożone przez co, ale strzeliłem, że chodzi pochodną z funkcji:
  
  $y={{4}^{x}}ln \left( 4arctgx \right)+\frac{{{4}^{x}}}{1+{{x}^{2}}}$
  
  Ruszam więc, stosując wzory i metody z mojego Kursu Pochodnych:
  
  ${y}'={{\left( {{4}^{x}}ln \left( 4arctgx \right)+\frac{{{4}^{x}}}{1+{{x}^{2}}} \right)}^{\prime }}={{\left( {{4}^{x}} \right)}^{\prime }}ln \left( 4arctgx \right)+{{4}^{x}}{{\left[ ln \left( 4arctgx \right) \right]}^{\prime }}+\frac{{{\left( {{4}^{x}} \right)}^{\prime }}\left( 1+{{x}^{2}} \right)-{{4}^{x}}{{\left( 1+{{x}^{2}} \right)}^{\prime }}}{{{\left( 1+{{x}^{2}} \right)}^{2}}}=$
  
  $={{4}^{x}}ln 4\cdot ln \left( 4arctgx \right)+{{4}^{x}}\frac{1}{4arctgx}{{\left( 4arctgx \right)}^{\prime }}+\frac{{{4}^{x}}ln 4\cdot \left( 1+{{x}^{2}} \right)-{{4}^{x}}\cdot 2x}{{{\left( 1+{{x}^{2}} \right)}^{2}}}=$
  
  $={{4}^{x}}\left[ ln 4cdot ln \left( 4arctgx \right)+\frac{1}{4arctgx}4\cdot \frac{1}{1+{{x}^{2}}}+\frac{\left( 1+{{x}^{2}} \right)ln 4-2x}{{{\left( 1+{{x}^{2}} \right)}^{2}}} \right]=$
  
  $={{4}^{x}}\left[ ln 4\cdot ln \left( 4arctgx \right)+\frac{1}{\left( 1+{{x}^{2}} \right)arctgx}+\frac{\left( 1+{{x}^{2}} \right)ln 4-2x}{{{\left( 1+{{x}^{2}} \right)}^{2}}} \right]$
2. Karolina
  28 stycznia 2013 at 11:59
  
  Tak wszystko się zgadza dziękuje bardzo za pomoc 🙂
Marcin
22 stycznia 2013 at 20:15

Witam Panie Krystianie!
Mam problem z pochodną f(x) = arctg \sqrt1-x/1+x
Czy mógłbym prosić Pana o pomoc.

Pozdrawiam

Odpowiedz
1. Krystian Karczyński
  24 stycznia 2013 at 10:16
  
  Jasne. Wynik w WolframAlpha jest tutaj:
  
  (arctg sqrt1-x/1+x)’
  
  A teraz dojdźmy do niego 🙂
  
  ${{\left( arctg\frac{1-x}{1+x} \right)}^{\prime }}=\frac{1}{{{\left( \tfrac{1-x}{1+x} \right)}^{2}}+1}{{\left( \frac{1-x}{1+x} \right)}^{\prime }}=\frac{1}{\tfrac{{{\left( 1-x \right)}^{2}}}{{{\left( 1+x \right)}^{2}}}+1}\frac{{{\left( 1-x \right)}^{\prime }}\left( 1+x \right)-\left( 1-x \right){{\left( 1+x \right)}^{\prime }}}{{{\left( 1+x \right)}^{2}}}=$
  
  $=\frac{-1\left( 1+x \right)-\left( 1-x \right)\cdot 1}{\left( \tfrac{{{\left( 1-x \right)}^{2}}}{{{\left( 1+x \right)}^{2}}}+1 \right){{\left( 1+x \right)}^{2}}}=\frac{-1-x-1+x}{{{\left( 1-x \right)}^{2}}+{{\left( 1+x \right)}^{2}}}=\frac{-2}{1-2x+{{x}^{2}}+1+2x+{{x}^{2}}}=$
  
  $=\frac{-2}{2+2{{x}^{2}}}=\frac{-2}{2\left( 1+{{x}^{2}} \right)}=-\frac{1}{1+{{x}^{2}}}$
  
  Jak ogólnie liczyć pochodne (także te z funkcji złożonych, jak tutaj), pokazałem w swoim Kursie:
  
  Kurs do Pochodnych Video
  
  Pozdrawiam!
Mateusz
21 stycznia 2013 at 23:14

Witam,
Ja również mam pytanie – czy mógłby mi Pan wytłumaczyć, dlaczego i w jaki sposób, z pochodnej : 3/x^4 wychodzi wynik : -12/x^5 ?
Byłbym wdzięczny 🙂

Odpowiedz
1. Konrad
  24 stycznia 2013 at 23:08
  
  3/(x^4)=3*x^(-4);
  pochodnia z x^y=y*x^(y-1)
  stąd:
  pochodna z 3*x(-4)=3*(-4)*x^(-4-1)= -12*x^(-5)
  czyli
  -12/(x^5)
  Mam nadzieję, że jasne.
  Pozdrawiam,
  Student Politechniki
2. Krystian Karczyński
  25 stycznia 2013 at 10:50
  
  Dzięki 🙂
Arek
21 stycznia 2013 at 15:26

Dzień dobry
Ja mam nieco inne pytanie, na które ciężko znaleźć klarowną odpowiedź. Jak oblicza sie numerycznie (za pomoca kalkulatora czy komputera) pochodna funkcji jednej zmiennej?

Z góry dziękuję za pomoc

Odpowiedz
1. Krystian Karczyński
  25 stycznia 2013 at 11:15
  
  Nie bardzo wiem, szczerze mówiąc, nigdy tego nie robiłem…
Paulina
21 stycznia 2013 at 14:29

a ja mam trochę inne pytanie. Czy pochodna z zera wynosi zero, czy nie istnieje?

Odpowiedz
1. Krystian Karczyński
  21 stycznia 2013 at 16:07
  
  Istnieje i wynosi zero, tak samo jak z każdej innej liczby (stałej).
Michał
20 stycznia 2013 at 17:49

Witam, w kursie badania zmienności funkcji w ostatniej lekcji (rysowanie wykresu + tabelka) bada Pan zmienność funkcji e^(x)/x^(2)

Mam wielki problem z obliczeniem drugiej pochodnej (potrzebnej do zbadania wklęsłości/wypukłości) tej funkcji, z pierwszą radzę sobie bez problemu, natomiast co do drugiej, to męczę się od dwóch godzin i za każdym razem wychodzi mi inny wynik, moi znajomi z kierunku też mają różne wyniki.
Bardzo Pana proszę o pomoc, gdyż w czwartek mam egzamin właśnie z badania zmienności funkcji. Wynik znam, bo porównując mianownik tej pochodnej otrzymał Pan jedno rozwiązanie, którym jest zero. Natomiast jak dojść do tego wyniku? Bardzo proszę o poświęcenie mi chwili, gdyż nie umiem sobie poradzić, pozdrawiam 🙂

ps: Wolfram niewiele pomaga

Odpowiedz
1. Krystian Karczyński
  25 stycznia 2013 at 11:37
  
  Przepraszam, już trochę po ptokach (tzn. po czwartku), ale odpowiem.
  
  To jest mój ulubiony przykład, bo kiedyś udzielałem dużo korepetycji studentom Akademii Morskiej w Szczecinie i tam był taki bardzo znany profesor (może obejdźmy się bez nazwisk…) który zawsze na poprawkach dawał do rozwiązania TEN właśnie przykład. Było z tym trochę śmiechu zawsze.
  
  No ale do rzeczy. Dlaczego WolframAlpha nie pomaga? Proszę zerknąć, wystarczy prosta formuła:
  
  (e^x/x^2)”
  
  No a teraz dojdźmy do wyniku krok po kroku. Kluczem do sukcesu będzie stałe porządkowanie wyników (wyciąganie przed nawias).
  
  Liczę pierwszą pochodną:
  
  ${{\left( \frac{{{e}^{x}}}{{{x}^{2}}} \right)}^{\prime }}=\frac{{{\left( {{e}^{x}} \right)}^{\prime }}{{x}^{2}}-{{e}^{x}}{{\left( {{x}^{2}} \right)}^{\prime }}}{{{\left( {{x}^{2}} \right)}^{2}}}=\frac{{{e}^{x}}{{x}^{2}}-{{e}^{x}}\cdot 2x}{{{x}^{4}}}=\frac{{{e}^{x}}x\left( x-2 \right)}{{{x}^{4}}}=\frac{{{e}^{x}}\left( x-2 \right)}{{{x}^{3}}}$
  
  Teraz drugą:
  
  ${{\left( \frac{{{e}^{x}}\left( x-2 \right)}{{{x}^{3}}} \right)}^{\prime }}=\frac{{{\left[ {{e}^{x}}\left( x-2 \right) \right]}^{\prime }}{{x}^{3}}-{{e}^{x}}\left( x-2 \right){{\left( {{x}^{3}} \right)}^{\prime }}}{{{\left( {{x}^{3}} \right)}^{2}}}=\frac{\left[ {{\left( {{e}^{x}} \right)}^{\prime }}\left( x-2 \right)+{{e}^{x}}{{\left( x-2 \right)}^{\prime }} \right]{{x}^{3}}-{{e}^{x}}\left( x-2 \right)3{{x}^{2}}}{{{x}^{6}}}=$
  
  $=\frac{\left[ {{e}^{x}}\left( x-2 \right)+{{e}^{x}} \right]{{x}^{3}}-3{{x}^{2}}{{e}^{x}}\left( x-2 \right)}{{{x}^{6}}}=\frac{{{e}^{x}}\left[ x-2+1 \right]{{x}^{3}}-{{e}^{x}}\left( x-2 \right)3{{x}^{2}}}{{{x}^{6}}}=\frac{{{x}^{3}}{{e}^{x}}\left( x-1 \right)-3{{x}^{2}}{{e}^{x}}\left( x-2 \right)}{{{x}^{6}}}=$
  
  $=\frac{{{x}^{2}}{{e}^{x}}\left[ x\left( x-1 \right)-3\left( x-2 \right) \right]}{{{x}^{6}}}=\frac{{{e}^{x}}\left[ {{x}^{2}}-x-3x+6 \right]}{{{x}^{4}}}=\frac{{{e}^{x}}\left( {{x}^{2}}-4x+6 \right)}{{{x}^{4}}}$
  
  No i tyle, powodzenia, polecam wszystkim mój Kurs, na którym krok po kroku na filmikach Video pokazuję, jak się robi takie rzeczy:
  
  Kurs Pochodne i Badanie Przebiegu Zmienności Funkcji
Kuba
16 stycznia 2013 at 19:53

witam, mam problem z przykładem ((1/x)^(sinx))^lnx . Czy tutaj trzeba użyć tego wzoru a^b=e^(blna)?
Oraz czy mógłby Pan pomóc z tym zadaniem : )
Pozdrawiam : )

Odpowiedz
1. Krystian Karczyński
  18 stycznia 2013 at 13:01
  
  Jasne, trzeba skorzystać z wzoru: ${{a}^{b}}={{e}^{bln a}}$ , a rozpisując krok po kroku pójdzie to tak:
  
  ${{\left[ {{\left( {{\left( \frac{1}{x} \right)}^{sin x}} \right)}^{ln x}} \right]}^{\prime }}={{\left[ {{\left( \frac{1}{x} \right)}^{sin x\cdot ln x}} \right]}^{\prime }}={{\left[ {{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}} \right]}^{\prime }}={{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}{{\left( sin x\cdot ln x\cdot ln \tfrac{1}{x} \right)}^{\prime }}=$
  
  $={{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}{{\left( sin x\cdot ln x\cdot ln \tfrac{1}{x} \right)}^{\prime }}={{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}\left[ {{\left( sin x \right)}^{\prime }}\left( ln x\cdot ln \tfrac{1}{x} \right)+sin x{{\left( ln x\cdot ln \tfrac{1}{x} \right)}^{\prime }} \right]=$
  
  $={{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}\left[ cos x\cdot ln x\cdot ln \tfrac{1}{x}+sin x\left( {{\left( ln x \right)}^{\prime }}\cdot ln \tfrac{1}{x}+ln x\cdot {{\left( ln \tfrac{1}{x} \right)}^{\prime }} \right) \right]=$
  
  $={{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}\left[ cos x\cdot ln x\cdot ln \tfrac{1}{x}+sin x\left( \frac{1}{x}\cdot ln \tfrac{1}{x}+ln x\cdot \frac{1}{\tfrac{1}{x}}{{\left( \frac{1}{x} \right)}^{\prime }} \right) \right]=$
  
  $={{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}\left[ cos x\cdot ln x\cdot ln \tfrac{1}{x}+sin x\left( \frac{ln \tfrac{1}{x}}{x}+ln x\cdot x\cdot \left( -\frac{1}{{{x}^{2}}} \right) \right) \right]=$
  
  $={{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}\left[ cos x\cdot ln x\cdot ln \tfrac{1}{x}+sin x\left( \frac{ln \tfrac{1}{x}}{x}-ln x\cdot \frac{1}{x} \right) \right]=$
  
  ${{e}^{sin x\cdot ln x\cdot ln \tfrac{1}{x}}}\left[ cos x\cdot ln x\cdot ln \tfrac{1}{x}+\frac{sin x\left( ln \tfrac{1}{x}-ln x \right)}{x} \right]$
  
  No i mam tylko nadzieję, że dobrze odczytałem zapis na początku…
2. Kamil
  4 grudnia 2013 at 15:35
  
  Witam, tak spoglądałem na komentarze i zauważyłem jak Pan tutaj wyliczał pochodną. Chciałbym się spytać Pana o dwie rzeczy:
  1. W pierwszej linijce na końcu skąd (z jakiego wzoru/własności) pochodna z e^(sin(x)*ln(x)*ln(1/x)) to ta sama liczba pomnożona przez pochodną wykładnika liczby e?
  2. W drugiej linijce na początku, jak mamy pochodną (sinx*lnx*ln(1/x) to na jej zapisanie korzystamy ze wzoru [ f(x) * g(x) ]’= f'(x)*g(x)+f(x)*g'(x) tylko czemu nie potraktujemy (sin*ln(x)) jako czynnik 1, a lnx(1/x) jako drugi? tylko samo sin(x) jako czynnik 1?
  3. Czy w takich sytuacjach jak pytaniu 2 (kiedy mamy wiele iloczynów), po zastosowaniu przemienności mnożenia pochodne będą takie same?
  
  Pozdrawiam serdecznie 🙂
Lena
7 stycznia 2013 at 22:49

Witam,
Mam obliczyć drugą pochodną z wyrażenia: 2^2+2x+lnx. I pierwsza pochodna wyszła mi taka: 4x+2+1/x. Licząc z tego drugą pochodną wychodzi 4+ ,,,, Własnie nie wiem jaka jest pochodna z 1/x 🙁

Odpowiedz
1. Krystian Karczyński
  16 stycznia 2013 at 11:00
  
  Dzień dobry, obawiam się, że już pierwsza pochodna wyszła Pani nieprawidłowa…
  
  ${{\left( {{2}^{2}}+2x+ln x \right)}^{\prime }}=2+\frac{1}{x}$
  
  Pochodna z ${{2}^{2}}$ równa jest zero, bo to pochodna z liczby, stałej (dwa do kwadratu to po prostu cztery). Pochodna z ${{x}^{2}}$ równa jest $2x$ , ale pochodna z ${{2}^{2}}$ równa się $0$ .
  
  Licząc dalej mamy:
  
  ${{\left( 2+\frac{1}{x} \right)}^{\prime }}=-\frac{1}{{{x}^{2}}}$
  
  …niech Pani zerknie np. na moje wzory do pochodnych – wzór numer 4.
Adam
11 grudnia 2012 at 14:49

Witam! Chcę tylko na początku dorzucić, że uwielbiam Pana i doceniam to co pan dla nas biednych studentów robi i dziękuję za to 🙂 I mam takie małe pytanie, przy obliczaniu pochodnej z a^x kalkulator wylicza a^x * log(2) a nie powinno byc a^x*ln(x)? ln zamiast log? bo to trochę zmienia postać rzeczy 🙂

Odpowiedz
1. Krystian Karczyński
  16 stycznia 2013 at 11:05
  
  A dzięki, dzięki, ale kalkulator wylicza ${{a}^{x}}log \left( a \right)$ jako wynik, a nie ${{a}^{x}}log \left( 2 \right)$ …
  
  No ale poza tym sprawa jest prosta i zwrócił Pan uwagę na ważny problem: w zachodnim zapisie matematycznym logx oznacza logarytm NATURALNY (czyli nasz lnx). Oni w ogóle nie używają zapisu lnx. Trzeba więc zawsze odpowiednio „tłumaczyć” wyniki.
  
  Więcej informacji o WolframAlpha może Pan zasięgnąć z mojego ebooka i filmików video:
  
  WolframAlpha – Praktyczny Przewodnik
Sebastian Stulej
11 grudnia 2012 at 00:40

Jak rozwiązać pochodzną x^x ?

Odpowiedz
1. Adam
  20 grudnia 2012 at 17:38
  
  Ponieważ nie ma takiego wzoru na pochodną jak x^x więc trzeba trochę pokombinować… można trzeba tez wzór rozpisać najlepiej jako e do jakiejś tam potęgi, a ponieważ a^(loga z b) = b więc e^(lnx)=x więc x już mamy i teraz to wszystko trzeba podnieść do potęgi x więc: (e^lnx)^x i korzystając z własności logarytmu wychodzi nam e^xlnx i liczysz jak pochodną funkcji złożonej e do. (e^xlnx)’ = e^xlnx * (lnx+x*(1/x)) (tam zastosowałem wzór na pochodną iloczynu) więc wychodzi ostatecznie
  (e^xlnx)*(lnx+1) ex można zamienić e^xlnx i wyjdzie prze arcy końcowy wynik: xlnx +x 🙂
2. Adam
  20 grudnia 2012 at 19:44
  
  ten prze racy końcowy wynik oczywiście źle podałem… 😉 ma być (x^x)lnx +(x^x)
Bartek
8 września 2012 at 17:39

Prosiłbym o pomoc w rozwiązaniu zadania mojego szalonego wykładowcy, który jak zwykle na ćwiczeniach i wykładach robił jedno a na
egzaminie drugie 😛

4. Dla jakiego n jest spełniona nierówność: [(x+n)/(x+1)]^x >7 Sorry, że to zadanie wrzuciłem pod stronę z kalkulatorem pochodnych, ale nie bardzo wiedziałem, gdzie indziej mogę o to zapytać. Z góry dzięki za pomoc

Odpowiedz
1. Bartek
  8 września 2012 at 17:41
  
  x -> nieskończoności
2. Krystian Karczyński
  10 września 2012 at 10:11
  
  Dzień dobry
  
  Jasne, rozumiem, że chodzi o nierówność:
  
  $\underset{x\to \infty }{\mathop{lim }}{{\left( \frac{x+n}{x+1} \right)}^{x}}>7$ ?
  
  Liczę sobie spokojnie granicę z lewej strony nierówności (poprzez dojście do wzoru na liczbę e):
  
  $\underset{x\to \infty }{\mathop{lim }}{{\left( \frac{x+n}{x+1} \right)}^{x}}=\underset{x\to \infty }{\mathop{lim }}{{\left( \frac{x+1-1+n}{x+1} \right)}^{x}}=\underset{x\to \infty }{\mathop{lim }}{{\left( 1+\frac{-1+n}{x+1} \right)}^{x}}=\underset{x\to \infty }{\mathop{lim }}{{\left[ {{\left( 1+\frac{-1+n}{x+1} \right)}^{x+1}} \right]}^{\frac{x}{x+1}}}=$
  
  Na boku liczę granicę z wykładnika potęgi:
  
  $\underset{x\to \infty }{\mathop{lim }}\frac{x}{x+1}=\underset{x\to \infty }{\mathop{lim }}\frac{x}{x\left( 1+\tfrac{1}{x} \right)}=1$
  
  Liczyli mam granicę po lewej stronie nierówności policzoną:
  
  $\underset{x\to \infty }{\mathop{lim }}{{\left[ {{\left( 1+\frac{-1+n}{x+1} \right)}^{x+1}} \right]}^{\frac{x}{x+1}}}={{\left[ {{e}^{-1+n}} \right]}^{1}}={{e}^{-1+n}}$
  
  Wracam się do nierówności:
  
  ${{e}^{-1+n}}>7$
  
  Jest to nierówność wykładnicza (z potęgą). Rozwiązuję ją logarytmując obie strony:
  
  ${{e}^{-1+n}}>7\quad ln \left( \ldots \right)$
  
  $ln {{e}^{-1+n}}>ln 7$
  
  $\left( -1+n \right)ln e>ln 7$
  
  $-1+n>ln 7$
  
  $n>ln 7+1$
  
  W zadaniu było gdzieś powiedziane, że $n$ musi być liczbą naturalną? Jeśli nie, to mam rozwiązanie, jeśli tak, to trzeba by jeszcze podumać nad tym, które liczby naturalne spełniają tą nierówność.
Kasia
5 września 2012 at 18:05

Dziękuje bardzo za pomoc;)

Odpowiedz
Kasia
3 września 2012 at 21:52

Wstawiłam pochodną z
y=ln2 −x2 * arctgx
i wyszło jakieś kompletne dziwactwo -2x^3 tan^-1 ?

Proszę o pomoc Panie Krystianie

Odpowiedz
1. Krystian Karczyński
  3 września 2012 at 22:37
  
  Wszystko jest chyba O.K. Rozumiem, że policzyć Pan chciał pochodną z: $y= ln 2-{{x}^{2}}arctgx$ – czy dobrze rozumiem?
  
  No to policzmy „ręcznie”:
  
  ${{\left( ln 2-{{x}^{2}}arctgx \right)}^{\prime }}={{\left( ln 2 \right)}^{\prime }}-{{\left( {{x}^{2}}arctgx \right)}^{\prime }}=-\left( {{\left( {{x}^{2}} \right)}^{\prime }}arctgx+{{x}^{2}}{{\left( arctgx \right)}^{\prime }} \right)=$
  
  $=-2xarctgx-\frac{{{x}^{2}}}{{{x}^{2}}+1}$
  
  W tym momencie Wolfram bardzo się stara „ułatwić” nam życie i przekształca ten wynik dalej, do wspólnego mianownika:
  
  $-2xarctgx-\frac{{{x}^{2}}}{{{x}^{2}}+1}=\frac{-2xarctgx\cdot \left( {{x}^{2}}+1 \right)}{{{x}^{2}}+1}-\frac{{{x}^{2}}}{{{x}^{2}}+1}=\frac{-2{{x}^{3}}arctgx-2xarctgx-{{x}^{2}}}{{{x}^{2}}+1}=\frac{-2{{x}^{3}}arctgx-{{x}^{2}}-2xarctgx}{{{x}^{2}}+1}$
  
  W amerykańskim zapisie matematycznym funkcje odwrotne do trygonometrycznych nie zaznacza się tak jak u nas przez np. arctgx, tylko jako ${{tan }^{-1}}x$ , czyli mamy Wolframowy:
  
  $\frac{-2{{x}^{3}}arctgx-{{x}^{2}}-2xarctgx}{{{x}^{2}}+1}=\frac{-2{{x}^{3}}{{tan }^{-1}}x-{{x}^{2}}-2x{{tan }^{-1}}x}{{{x}^{2}}+1}$
2. Kasia
  4 września 2012 at 10:58
  
  miało być (ln2^-x^2) * arctgx
  ln2 do potęgi -x do potęgi 2 i to wszystko razy arctgx
  Więc przepraszam za błąd w zapisie i czy mogłabym jeszcze raz poprosić o pomoc ?
3. Krystian Karczyński
  5 września 2012 at 08:42
  
  Hmmm… Czyli w ten sposób: $ln {{2}^{-{{x}^{2}}}}arctgx$ ?
4. Kasia
  5 września 2012 at 10:51
  
  tak 😉
5. Krystian Karczyński
  5 września 2012 at 15:17
  
  No to troszkę dziwnie, ale liczę (przed rzuceniem się na pochodne korzystam z własności logarytmu)…
  
  ${{\left( ln {{2}^{-{{x}^{2}}}}arctgx \right)}^{\prime }}={{\left( -{{x}^{2}}ln 2arctgx \right)}^{\prime }}=-2x\cdot ln 2\cdot arctgx-{{x}^{2}}ln 2\cdot \frac{1}{1+{{x}^{2}}}=-2x\cdot ln 2\cdot arctgx-\frac{{{x}^{2}}ln 2}{1+{{x}^{2}}}$
  
  Tutaj niestety Wolfram znowu próbuje bardzo na siłę „ułatwić” Pani życie i sprowadza do wspólnego mianownika:
  
  $-2x\cdot ln 2\cdot arctgx-\frac{{{x}^{2}}ln 2}{1+{{x}^{2}}}=\frac{-2x\cdot ln 2\cdot arctgx\cdot \left( 1+{{x}^{2}} \right)}{1+{{x}^{2}}}-\frac{{{x}^{2}}ln 2}{1+{{x}^{2}}}=\frac{-2x\cdot ln 2\cdot arctgx-2{{x}^{3}}\cdot ln 2\cdot arctgx-{{x}^{2}}ln 2}{1+{{x}^{2}}}=\frac{-2x\cdot ln 2\cdot arctgx-2{{x}^{3}}\cdot ln 2\cdot arctgx+ln {{2}^{-{{x}^{2}}}}}{1+{{x}^{2}}}$
  
  No i zamieniając kolejność w liczniku i pamiętając o tym, że w Stanach $arctgx={{tan }^{-1}}x$ i $ln x=log \left( x \right)$ mamy Wolframowy:
  
  $\frac{-2{{x}^{3}}log \left( 2 \right)\cdot {{tan }^{-1}}x+log \left( {{2}^{-{{x}^{2}}}} \right)-2xlog \left( 2 \right){{tan }^{-1}}x}{1+{{x}^{2}}}$
Stanisław
7 czerwca 2012 at 08:09

Witam Panie Krystianie,
czy nie zna Pan jakiegoś kalkulatora do liczenia pochodnych cząstkowych wielu zmiennych?

Dziękuję za pomoc i pozdrawiam:)

Odpowiedz
Michał
19 maja 2012 at 02:36

Ja mam problem z pochodną lnx-1/(lnx)^2 Jak to obliczyć ?
proszę o pomoc i pozdrawiam

Odpowiedz
1. Krystian Karczyński
  21 maja 2012 at 08:35
  
  Jasne, trzeba najpierw skorzystać z wzoru na dzielenie, a potem na funkcję złożoną:
  
  ${{\left( \frac{ln x-1}{{{ln }^{2}}x} \right)}^{\prime }}=\frac{{{\left( ln x-1 \right)}^{\prime }}{{ln }^{2}}x-\left( ln x-1 \right){{\left( {{ln }^{2}}x \right)}^{\prime }}}{{{\left( {{ln }^{2}}x \right)}^{2}}}=\frac{\tfrac{1}{x}{{ln }^{2}}x-\left( ln x-1 \right)2ln x\cdot \tfrac{1}{x}}{{{ln }^{4}}x}=$
  
  $=\frac{\tfrac{{{ln }^{2}}x}{x}-\tfrac{2ln x\left( ln x-1 \right)}{x}}{{{ln }^{4}}x}=\frac{{{ln }^{2}}x-2ln x\left( ln x-1 \right)}{x{{ln }^{4}}x}=\frac{ln x\left[ ln x-2\left( ln x-1 \right) \right]}{x{{ln }^{4}}x}=\frac{-ln x+2}{x{{ln }^{3}}x}$
2. Paweł
  7 listopada 2017 at 17:42
  
  jak wprowadzić funkcję xe^4x
Łukasz
8 maja 2012 at 21:47

Witam
Mam pewien problem
Bo zupełnie nie wiem dlaczego $\frac{-1}{{{x}^{2}}+1}$ ma pochodną $\frac{2x}{{{x}^{2}}+1}$ ?
Prosiłbym o małą pomoc;)

Odpowiedz
1. Krystian Karczyński
  9 maja 2012 at 06:59
  
  Dzień dobry
  
  No trochę niezupełnie, pochodna z $\frac{-1}{{{x}^{2}}+1}$ to $\frac{2x}{{{\left( {{x}^{2}}+1 \right)}^{2}}}$ , a nie $\frac{2x}{{{x}^{2}}+1}$ .
  
  Bierze się to – na przykład – z elementarnego wzoru ${{\left( \frac{a}{x} \right)}^{\prime }}=-\frac{a}{{{x}^{2}}}$ .
  
  Licząc z tego wzoru i traktując funkcję ${{x}^{2}}+1$ jako funkcję wewnętrzną i przyjmując $a=-1$ mam:
  
  ${{\left( \frac{-1}{{{x}^{2}}+1} \right)}^{\prime }}=-\frac{-1}{{{\left( {{x}^{2}}+1 \right)}^{2}}}{{\left( {{x}^{2}}+1 \right)}^{\prime }}=\frac{1}{{{\left( {{x}^{2}}+1 \right)}^{2}}}2x=\frac{2x}{{{\left( {{x}^{2}}+1 \right)}^{2}}}$
  
  Można też skorzystać z normalnego wzoru na dzielenie:
  
  ${{\left( \frac{-1}{{{x}^{2}}+1} \right)}^{\prime }}=\frac{{{\left( -1 \right)}^{\prime }}\left( {{x}^{2}}+1 \right)-\left( -1 \right){{\left( {{x}^{2}}+1 \right)}^{\prime }}}{{{\left( {{x}^{2}}+1 \right)}^{2}}}=\frac{0\cdot \left( {{x}^{2}}+1 \right)+2x}{{{\left( {{x}^{2}}+1 \right)}^{2}}}=\frac{2x}{{{\left( {{x}^{2}}+1 \right)}^{2}}}$
Basia
28 lutego 2012 at 13:10

Panie Krystianie,
zupełnie nie wiem dlaczego pochodna z x^sinx wychodzi

[x^(sinx-1)][sinx + lnxcosx]

licząc tą pochodną zatrzymuję się w momencie: [x^sinx][sinx/x +cosxlnx], korzystam ze wzoru: a^b = e^blna

Odpowiedz
1. Krystian Karczyński
  28 lutego 2012 at 18:43
  
  A w tej tzw. „prawidłowej odpowiedzi” nie powinno być x przed lnxcosx? Tzn. xlnxcosx zamiast lnxcosx?