Jak to wyglądało z „normalnymi” pierwiastkami?
Mając daną do policzenia granicę, do której jakoś zamieszane było jakieś odejmowanie z pierwiastkiem (i której nie dało się obliczyć prościej, rzecz jasna), czyli:
„COŚ – pierwiastek z czegoś”
„pierwiastek z czegoś – COŚ”
„pierwiastek z czegoś – pierwiastek z czegoś”
stosowaliśmy sztuczkę, którą ja nazywam – „mnożenie przez sprzężenie”.
Po prostu mnożyliśmy to wyrażenie przez jego odpowiednik ze znakiem plus, a właściwie przez ułamek, w którym był ten odpowiednik w liczniku i mianowniku.
Na przykład:
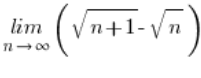 mnożyliśmy tak:
mnożyliśmy tak: 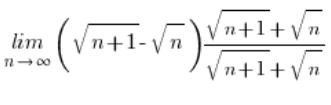
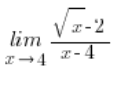 mnożyliśmy tak:
mnożyliśmy tak: 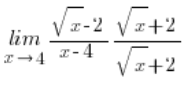
Sprytna ta sztuczka pozwalała nam wyjść na wzór skróconego mnożenia:
![]()
Po wyjściu na ten wzór kwadraty „kosiły” pierwiastki i wychodziliśmy na prostą (no powiedzmy, czasami trochę dłuższą prostą).
Co jednak z sytuacją, kiedy pierwiastki zamieszane w odejmowanie będą trzeciego stopnia? Tak jak na przykład tutaj:
\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}Standardowa metoda postępowania, tzn. mnożenie w następujący sposób:
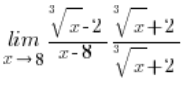
Nic nam nie da, bo tym razem w liczniku po wyjściu na wzór:
![]()
Kwadraty w żaden sposób nie „skrócą” na pierwiastków trzeciego stopnia. Czyli będziemy dalej w kropce.
Jak będzie to wyglądać z pierwiastkami trzeciego stopnia?
W przypadku odejmowania z pierwiastkami trzeciego stopnia trzeba po prostu „celować” w zupełnie inny wzór (ale też z gimnazjum), mianowicie:
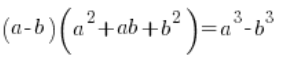
Czyli nasze dane ![]() (w którym a lub b lub oba to pierwiastki trzeciego stopnia) zamiast mnożyć przez
(w którym a lub b lub oba to pierwiastki trzeciego stopnia) zamiast mnożyć przez ![]() mnożyć będziemy przez
mnożyć będziemy przez ![]() i po zastosowaniu wzoru trzecie potęgi zrobią swoją robotę, „skracając” pierwiastki.
i po zastosowaniu wzoru trzecie potęgi zrobią swoją robotę, „skracając” pierwiastki.
Przykład 1
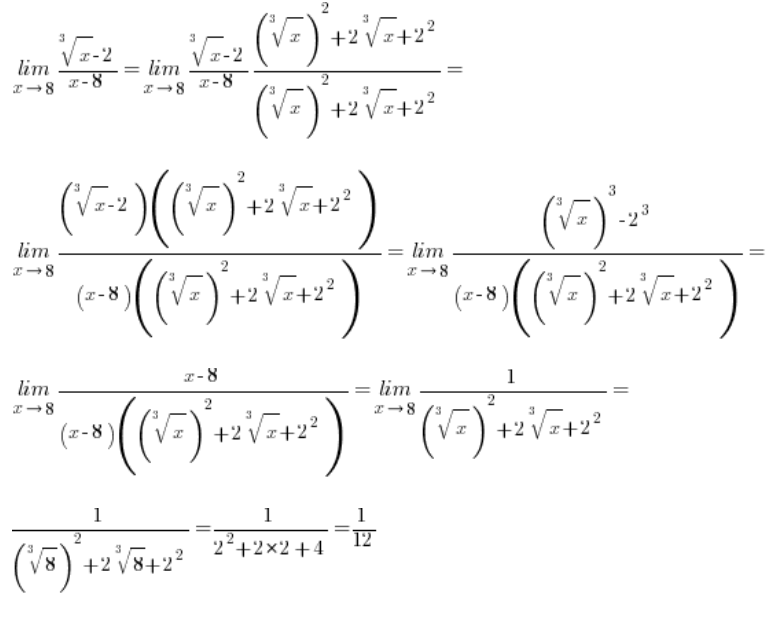
Przykład 2
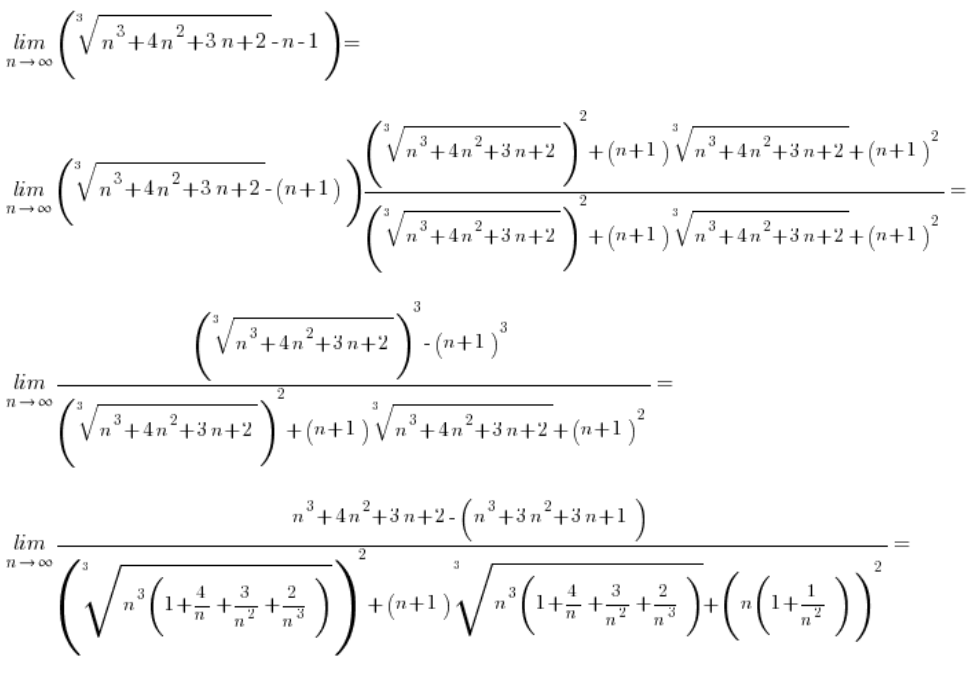
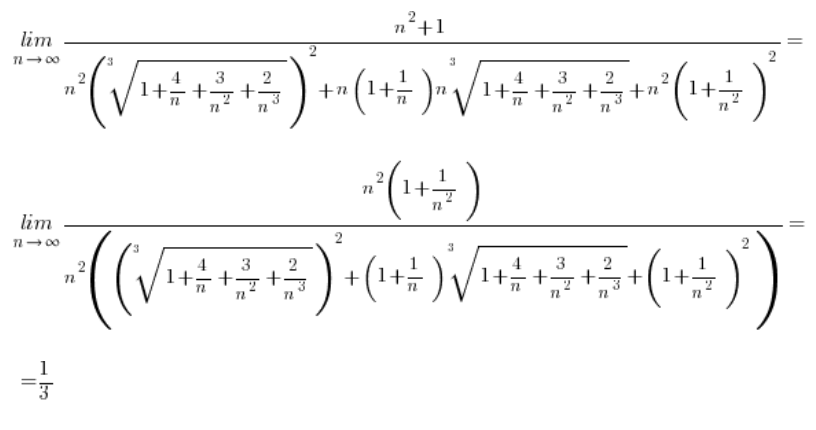



31 Komentarzy
Aleksandra
no dobra wszystko fajnie, ale co kiedy jeden pierwiastek jest 2 stopnia a drugi 3 stopnia. Wzory stosowac po kolei? najpierw na 3 potege potem na 2 czy jest jakis inny magiczny sposob?
Pozdrawiam
Alex
co zrobić z pierwiastkami z kursu granic z pracy domowej nr 7 zad 2 przyklad 15 ?
Krystian Karczyński
Witam. Trzeba „podprowadzić” to do wzoru \underset{x\to 0}{\mathop{lim }}\frac{ln \left( 1+x \right)}{x}=1, w następujący sposób:
\underset{x\to 0}{\mathop{lim }}\frac{ln \left( 1+\sqrt{x} \right)}{\sqrt[3]{x}}=\underset{x\to 0}{\mathop{lim }}\frac{\frac{ln \left( 1+\sqrt{x} \right)}{\sqrt{x}}\cdot \sqrt{x}}{\sqrt[3]{x}}=\underset{x\to 0}{\mathop{lim }}\frac{ln \left( 1+\sqrt{x} \right)}{\sqrt{x}}\frac{\sqrt{x}}{\sqrt[3]{x}}=\underset{x\to 0}{\mathop{lim }}\frac{ln \left( 1+\sqrt{x} \right)}{\sqrt{x}}\frac{{{x}^{\tfrac{1}{2}}}}{{{x}^{\tfrac{1}{3}}}}=\underset{x\to 0}{\mathop{lim }}\frac{ln \left( 1+\sqrt{x} \right)}{\sqrt{x}}{{x}^{\frac{1}{6}}}=1\cdot 0=0[/latex]
xxxx
Jak powstal licznik w trzecim dzialaniu w drugiej linijce? (druga linijka od góry można to jakos bardziej zrozumiale rozpisac?)
Krystian Karczyński
Przykro mi, nie bardzo wiem, o które trzecie działanie chodzi… Drugą linijkę od góry całego postu? Czy drugą linijkę od góry przykładu 1?
Ralf
granica ciągu:(pierwiastek 3go stopnia z (n^3+8))-(pierwiastek 2go stopnia z (n^2+4)
Mateusz
Cześć Krystian, mam pytanie do przykładu 10 z mnożenia przez sprzężenie. Czy aby na pewno wynik powinien tam wyjść 2? Mi wychodzi 3 i nie mogę znaleźć błędu w swoich obliczeniach. Może to u Ciebie jest literówka w odpowiedziach? Jeżeli się mylę, to daj znać, pójdę z przykładem na konsultacje. Twoje kursy bardzo pomagają studen\tom, zwłaszcza informatyki. Dzięki!
Mateusz
Ah, sam znalazłem błąd. Miałem wielomian postaci 6(xxx)/2(xxx) i za szybko wyłączyłem sobie 6/2 przed ułamek. Wszystko się zgadza, wynik równy 2. 🙂
Krystian Karczyński
O.K. Dobrze, że się zgadza 🙂
Heniek
Witam. Też mam problem z tym przykładem (ZDL2, przykład 10). Jakbym nie liczył wychodzi mi 3. Gdzie robię błąd?
Krystian Karczyński
Dzień dobry
Tam powinno wyjść 3 🙂
Jeśli ma Pan wersję Kursu z błędem to bardzo przepraszam. Tutaj wklejam rozwiązanie tego przykładu krok po kroku:
https://twitter.com/etrapez/status/248680865436147714/photo/1
Mateusz
Witam:) Widzę, że kursy Pana Krystiana są z dnia na dzień coraz bardziej popularne. Bardzo dobrze. Kończę powoli 3 semestr. Pozdrawiam
Krystian Karczyński
Cześć, powodzenia w dalszych bojach a studiach!
Michał
Muszę zgodzić się z użytkownikiem „Mac”. Kursy eTrapez tworzone przez Pana Krystiana są najlepszym dla stundenta źródłem nauki by szybko pojąć temat. Szereg różych przykładów, sposobów, metod rozwiązywania. Dodatkowo wielki plus za luźne podejście to mega motywuje.
Krystian Karczyński
Dzięki!
Mikołaj
Chyba, że profesor jest cięty na Krystianowe sposoby 😛
Artur
Witam.
Właśnie zdałem egzamin na 5.0! Bazując jedynie na Twoich kursach + coś tam ze szkoły średniej.
Dodam, że studiuje informatyke na agh-u.
Wielkie dzięki:)
Oby więcej takich ludzi jak Ty.
Pozdrawiam.
Krystian Karczyński
Super, gratuluję!
Krystian Karczyński
Ale dlaczego w liczniku miała by zostać liczba?
Mac.
Powiem Ci szczerze Krystian (skoro Ty się do mnie na „Ty” zwracasz to ja też będę :D) Na prawdę Twoje kursy pomagają. Mają taki ciekawy przekaz że nawet matematyka i oglądanie lekcji po ~2h staje się ciekawe. Rządzisz. Jest tylko jedne skromne „ale” z Twoim blogiem i stroną…
Krystian Karczyński
Dzięki. Nie byłbym sobą, gdybym nie spytał o te skromne „ale”… ? 🙂
Mac.
Jest „kapke” dziurawa :/ Treściwa i w ogóle ale ma parę błędów np. Gdy wyskakuje formularz e-mailingowy można dowolnie poruszać stroną – poszerzać itp. Z tego co zauważyłem strona była robiona zewnętrzne a blog to jakiś gotowiec. Przez to są takie małe dziury ale generalnie spoko jest 😀 Zrozumiałe jest że nacisk kładziesz na kursy a nie na stronkę i blogaska 🙂
Krystian Karczyński
Co do bloga, to szykuje się Wielka Nowa Odsłona… 🙂
Mac.
No mam nadzieję 😀 bo trochę dziur jest które mogą nie miło namieszać. Ciekawi mnie co Cie natchnęło żeby zacząć czymś takim się zajmować.
Krystian Karczyński
Wezmę się za te dziury 🙂
Kilka lat temu udzielałem bardzo \intensywnie korepetycji i szukałem jakiegoś sposobu, żeby robić to lepiej i inaczej. Pewnego dnia u znajomego co miał 350 programów TV w kablówce, w jakimś bardzo mało popularnym kanale edukacyjnym (ale polskim) przypadkiem włączyłem na Pana, który na kartce papieru tłumaczył do kamery, jak się liczy macierze odwrotne. Pomyślałem, że robi dokładnie to samo co ja i to w telewizji. Kilka miesięcy później siedząc na korepetycjach przyszła mi myśl „z niczego”, że mogę to co robię na korepetycjach, robić w Internecie. Strasznie się zapaliłem do tego pomysłu i tak się zaczęło 🙂
Łukasz
Człowieku jesteś mistrzem! W tydzień opanowałem, granice i pochodne wraz z ich wszystkimi tematami dzięki Tobie! Naprawdę gratuluje pomysłu i zarazem dziękuję 🙂
Krystian Karczyński
Dzięki, powodzenia na studiach!
A.
Mario: A mnie wyszło 3.
Wyciagasz n przed nawias i w ułamku masz n(3-1/n)*n(3+2/n) / n^2(1-1/n^2) (To wszystko pod pierwiastkiem). Obydwa n z licznika skracają się z n2 z mianownika. 1/n dązy do zera, podobnie jak 2/n. Mianownik dazy do jednyki. I pod pierwiastkiem zostaje 3*3/1. Czyli pierwiastek z 9. A to jest rowne 3.
Krystian Karczyński
Dzięki, zgadza się 🙂
Jacek
jak na moje oko, to ten drugi przykład jest źle, bo jest pomnożony tylko przez sprzężenie, a noe przez a^2+ab+b^2… chyba ze się mylę?
Krystian Karczyński
Oczywiście, ma Pan dobre oko! Bardzo, bardzo przepraszam za moją pomyłkę (już poprawiłem), wyszłoby w sumie, że sam sobie dokładnie zaprzeczam, ech…