Trudniejsze granice funkcji do policzenia wymagają często podstawienia, na przykład:
Przykład
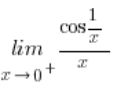
Granica w liczniku nie istnieje, w mianowniku zbiega do zera… Do czego zmierza całość?
Dogodnym podstawieniem będzie: 
Z podstawienia wynika, że: 
I że jeśli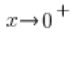 
, to 
. Mamy więc:
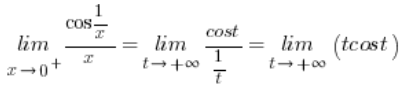
A ta granica nie istnieje, co można udowodnić w sposób pokazany w innym moim poście.
