Pochodne kierunkowe – znowu coś nowego?
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Miejsce i czas akcji
Obliczanie pochodnych kierunkowych jako temat do przerobienia (czyli do zaliczenia) plasują się właściwie tuż po pochodnych cząstkowych funkcji wielu zmiennych, które większość studentów przerabia w II semestrze.
Jest to temat na tyle rzadko jednak podejmowany, że nie uwzględniłem go w swoim Kursie do pochodnych cząstkowych i na tyle często, że wrzucę go na bloga – ku pożytkowi tych, którzy pochodnych kierunkowych nauczyć się muszą i tych, którzy są po prostu ciekawi, o co chodzi. Zaznaczam jednak, że tak jak w Kursach skoncentruję dzisiaj prawie wyłącznie na praktyce (“jak ja mam to zrobić?”), a nie na teorii (“co ja właściwie robię?”).
Pochodne kierunkowe – jak ja mam to zrobić?
W przypadku pochodnej kierunkowej mamy do czynienia z jednoczesnym przyrostem argumentów x i y, któremu oczywiście odpowiada pewien przyrost wartości funkcji 
.
Do zadania potrzebujemy trzech rzeczy:
- Funkcji, z której będziemy liczyć pochodną kierunkową.
- Punktu, w którym będziemy liczyć pochodną kierunkową.
- Kierunku danym w postaci wektora.
Mając powyższe, zadanie sprowadza się do przerobienia wektora na wektor kierunkowy (coś z geometrii analitycznej, pokażę jak to zrobić za moment), a potem wstawienia do wzoru:
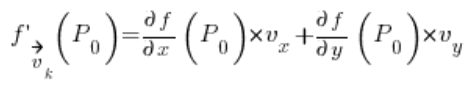
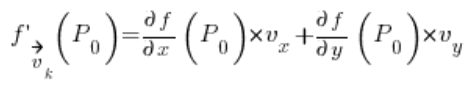
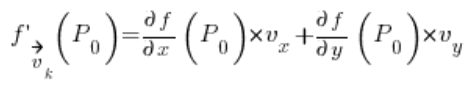
W którym:
to pochodna kierunkowa w punkcie 
w kierunku wektora 
to punkt, w którym liczymy pochodną kierunkową
to współrzędne wektora kierunkowego
to pochodne cząstkowe funkcji w punkcie .
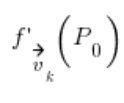
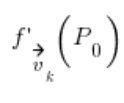
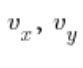
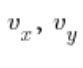
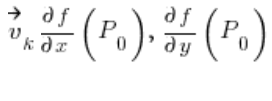
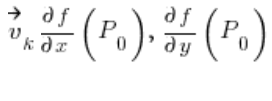
Oblicz pochodną kierunkową funkcji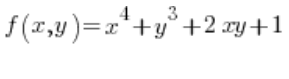 
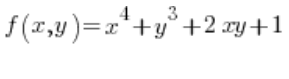
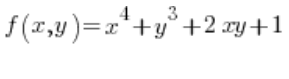
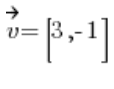
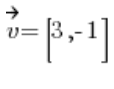
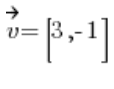
w punkcie P(1,2) w kierunku 
.
Rozwiązanie:
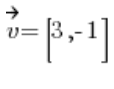
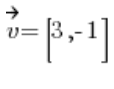
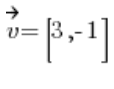
Wszystko jest dane na tacy, tylko z wektora trzeba zrobić wektor kierunkowy.
Wektor kierunkowy to wektor o takim samym kierunku (kto by pomyślał), zwrocie, ale o długości 1.
Oblicza się go ze wzoru:
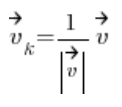
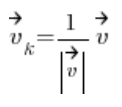
Czyli po prostu dzieli jego współrzędne przez jego długość.
No to liczymy długość wektora :
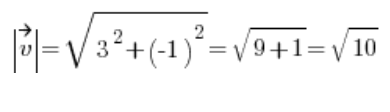
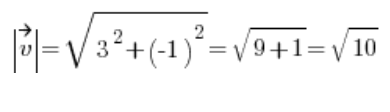
Po czym wychodzimy na wektor kierunkowy:
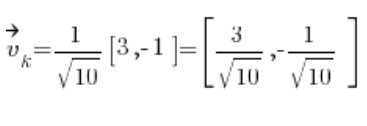
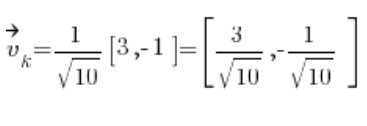
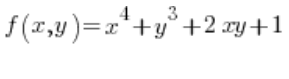
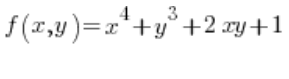
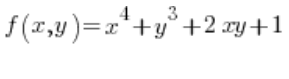
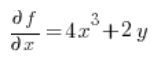
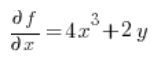
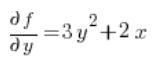
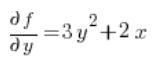
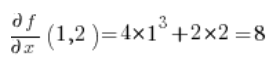
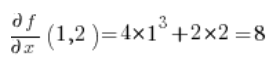
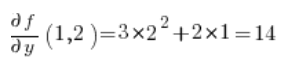
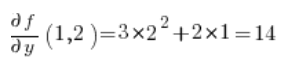
Do wzoru na pochodną kierunkową potrzebna nam będą jeszcze pochodne z funkcji w punkcie P(1,2):
No i mamy wszystko, co potrzebne jest do wzoru:
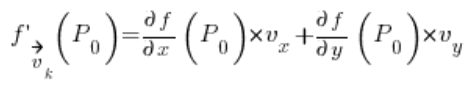
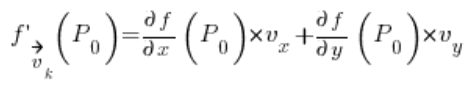
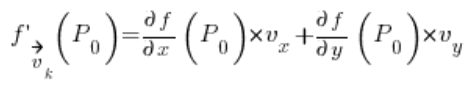
Podstawiamy tylko i mamy wynik: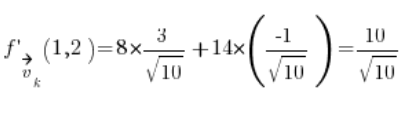 
.
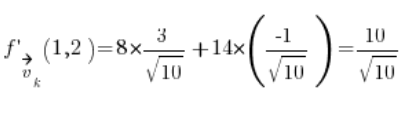
Zrobione.
Przykład 2
Znajdź pochodną kierunkową funkcji: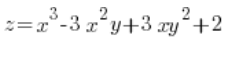 
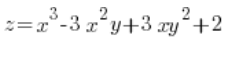
w punkcie P(3,1) w kierunku od tego punktu do punktu Q(6,5).
Rozwiązanie:
Sprawa o tyle trudniejsza, że wektor kierunku nie jest dany wprost, ale cóż to dla nas.
Przesuwamy się od punktu P do punktu Q, wektor przesunięcia więc to wektor [3,4].
Teraz szukamy wektora kierunkowego licząc długość wektora [3,4]:
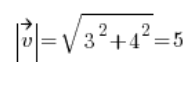
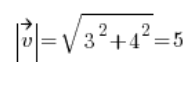
I mamy wektor kierunkowy:
Teraz liczymy pochodne cząstkowe w punkcie (3,1):
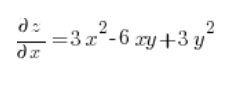
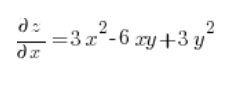
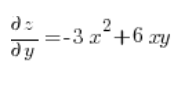
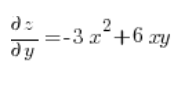
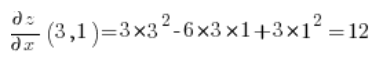
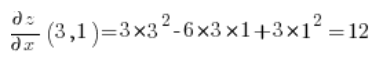
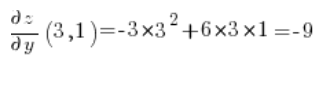
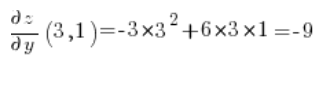
No i podstawiamy tylko do wzoru na pochodną kierunkową:
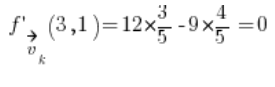
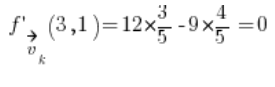
Przykład 3
Znajdź pochodną kierunkową funkcji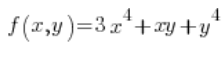 
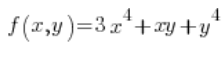
w punkcie (1,2) w kierunku tworzącym z dodatnią półosią X kąt 
.
Rozwiązanie:
Zadanie niby trudniejsze, ze względu na brak w danych wektora kierunku. Narysujmy jednak całą rzecz:
Rozchodzi się o to, żeby znaleźć współrzędne byle jakiego wektora o zaznaczonym kierunku.
Korzystamy z tego, że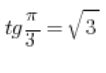 
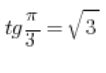
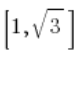
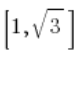
i możemy przyjąć sobie, że nasz wektor ma współrzędne 
, jak na rysunku (wystarczyło wybrać byle jaki wektor o kierunku jak kierunek prostej):
No i teraz już po staremu.
Liczymy wektor kierunkowy:
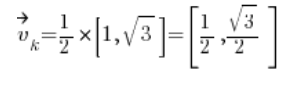
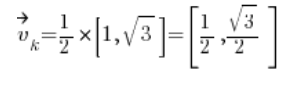
Potem pochodne cząstkowe w punkcie (1,2):
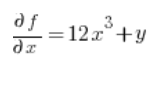
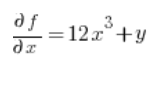
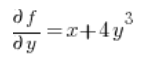
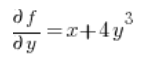
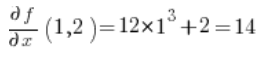
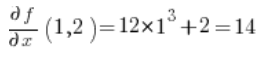
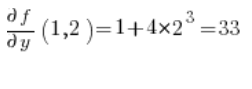
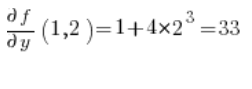
Podstawiamy do wzoru i mamy wynik
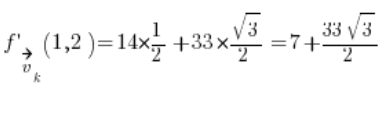
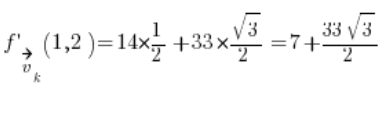
Zapraszam do pytań w komentarzach – jak zawsze 🙂
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
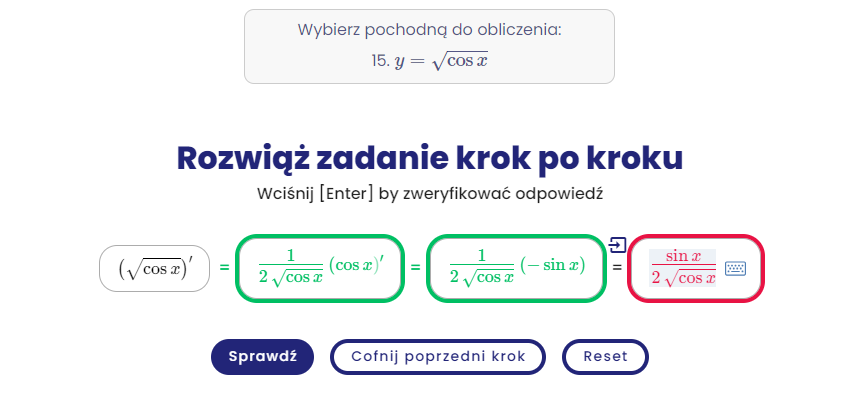
Obliczyć pochodną funkcji 𝑓(𝑥, 𝑦) = 𝑙𝑛√(𝑥^2+𝑦^2) w punkcie (−3,4) w kierunku wersora tworzącego kąt 𝜋/3 z dodatnią pólosią Ox.
Jak rozwiązać to zadanie? Jest dosyć podobne do tego z przykładu 3 ale nie potrafię go rozwiązać
A w jaki sposób rozwiązać zadanie gdzie trzeba policzyć pochodną cząstkową w punkcie ale nie ma nic o żadnym wektorze? Znalazłam na forum tu: że trzeba policzyć pochodną kierunkową w tym punkcie… Ale jak to skoro nie ma żadnego wektora?
Dlaczego kiedy w przykładzie trzecim zamiast vektora [1, \sqrt(3) ] użyłem [sqrt(3),1] wyszedł inny wynik? Przecież kierunek tego wektora i długość tego wektora jest taka sama, prawda?
czy mógłbyś dodać do bloga kalkulator do owych funkcji ?
Wyznaczyć wszystkie wersory v dla których pochodna kierunkowa funkcji f(x,y)= ln(xy^2)/x w punkcie (e,e) w kierunku wersora v = 2/e^2 . Jak poradzić sobie z takim zadaniem ?:)
Witam! Nie wiem czy Pana sposób można zastosować do przykładu, w którym mamy policzyć pochodną kierunkową funkcji f(x,y)=(x^4 + (y-1)^4)^(1/4) w kierunku wektora (1/2^(1/2);1/2^(1/2)) w punkcie (0,1). Pochodne w tym punkcie się zerują i wychodzi wynik 0. Czy to jest poprawnie?
Dziękuję i pozdrawiam!
Witam serdecznie, mam pytanie czy znajdę w Pana kursach rozwiązania takich zadań jak:
1.Zbadaj różniczkowalność funkcji?
f(x,y) =xy/(1+|x|+|y|)
Pozdrawiam serdecznie
Witam,
Mam problem z podobnym zadaniem. Znajdz df(1, 1, 1) oraz pochodna w punkcie (1, 1, 1) w kierunku wektora (3, 2, 1) funkcji
f(x, y, z) = x/y + y/z. Z Pana nieopisaną pomocą chyba poradziłam sobie z częścią drugą zadania tzn(Znajdz pochodna w punkcie (1, 1, 1) w kierunku wektora (3, 2, 1) funkcji f(x, y, z) = x/y + y/z) Wyszło mi 4/pierwiastek z 14. Ale niestety w ogole nie wiem jak mam się zabrać za pierwszą część zadania co to jest df(1, 1, 1)? Pochodna funkcji x/y +y/z w punkcie (1,1,1)?
Mam jeszcze jedno zadanie które sprawia mi dużo problemów: Niech f = f(t, u, v) — funkcja rózniczkowalna. Policzyc pochodne czastkowe funkcji
g(x, y) = f(x^2 + y^2, x^2 − y^2, 2x). Tutaj to już w ogóle nie mam pomysłu 🙁
Byłabym wdzięczna gdyby mi Pan pomógł 🙂 Z góry dziękuję i pozdrawiam 🙂
Panie Krystianie, odnośnie pierwszego przykładu, podobne zadanie jest w książce Banaś Wędrychowicz “Zbiór zadań z analizy matematycznej” (str. 77 zad.54), tyle że tam w odpowiedzi nie ma pierwiastka, jak u Pana. Mógłby Pan jeszcze raz wytłumaczyć dlaczego on tam musi być ?
Jak tu jest to prosto i fajnie opisane. Czemu znalazłem to dopiero w trakcie “kampani wrześniowej”. Naprawde pomagasz !! Dziękuję
PS. filmiki na youtube bardzo pomocne
Witam Panie Krystianie,
jeżeli przy funkcji dwóch zmiennych mam podane jedynie nachylenie kąta do osi OX, to nachylenie do osi OY bedzie wynosić 90 odjąć nachylenie do OX ?
Świetny artykuł, idealna pomoc dla studentów!
Jedno małe “ALE” symbol “x” jako operacja mnożeina bardzo mylący z iloczynem wektorowym !
Witam!
Mam problem z takim zadaniem:
Wyznaczyć taki wersor aby pochodna kierunkowa w pukcie (1,-1) była równa 1. dla funkcji f(x,y)=x^2+y^2. dla jakiego wersora pochodna kierunkowa w punkcie (1,-1) przyjmuje największą wartość? jaka jest ta wartość?
Z góry dziękuję za pomoc.
Mam do rozwiązania takie zadanie:
Oblicz pochodną funkcji f(x,y,z)=x√y ∛(z^2 ) e^(-√x+y-z^2 ) w punkcie P(1,1,1) w kierunku wektora l=[√2/3,√3/3, cosβ]
Witam,
Czy dobrze rozumiem, że zapis ∇⋅(f*v) można utożsamiać z pochodną kierunkową? (v to oczywiście nasz wektor).
Jest to część równania z którego mam wyznaczyć wektor v. Czy da się to zrobić?
Pozdrawiam i z góry dziękuję (choć ostatnio mało aktywny ten wątek).
Dzień dobry,
mam jedno pytanie, jak rozwiązać zadanie w którym należy policzyć pochodną kierunkową w kierunku dowolnego wektora?
Z góry bardzo dziękuję za pomoc ;))
A jak obliczyć takie zdanie:
Oblicz pochodną kierunkową funkcji f(x,y)= x^(y^2)w punkcie (1,1) w kierunku osi OX ?
Standardowo ze wzoru:
{{{f}’}_{{{{\vec{v}}}_{k}}}}\left( {{P}_{0}} \right)=\frac{\partial f}{\partial x}\left( {{P}_{0}} \right)\cdot {{v}_{x}}+\frac{\partial f}{\partial y}\left( {{P}_{0}} \right)\cdot {{v}_{y}}
z tym, że jeśli mamy liczyć w kierunku osi OX przyjmujemy sobie za wektor kierunkowy wersor {{\vec{v}}_{k}}=\left[ 1,0 \right]– zwróć uwagę, że jest to dokładnie wektor o kierunku osi OX i długości 1, czyli wektor kierunkowy.
Teraz już tylko liczymy odpowiednie pochodne metodami pokazanymi w moim Kursie Funkcji Wielu Zmiennych:
\frac{\partial f}{\partial x}={{\left( {{x}^{{{y}^{2}}}} \right)}^{\prime }}={{y}^{2}}{{x}^{{{y}^{2}}-1}}– przykład w WolframAlpha
\frac{\partial f}{\partial y}={{\left( {{x}^{{{y}^{2}}}} \right)}^{\prime }}={{x}^{{{y}^{2}}}}ln x\cdot {{\left( {{y}^{2}} \right)}^{\prime }}=2y{{x}^{{{y}^{2}}}}ln x– przykład w WolframAlpha
oraz wartości tych pochodnych w punkcie \left( 1,1 \right):
\frac{\partial f}{\partial x}\left( 1,1 \right)={{1}^{2}}{{1}^{{{1}^{2}}-1}}=1
\frac{\partial f}{\partial y}\left( 1,1 \right)=2\cdot 1\cdot {{1}^{{{1}^{2}}}}ln 1=0
Podstawiamy wszystko do wzoru i mamy wynik:
{{{{f}’}}_{\left[ 1,0 \right]}}\left( 1,1 \right)=1\cdot 1+0\cdot 0=1
Witam.
Dziękuje Panie Krystianie za ten temat, dzięki niemu zaliczyłem koło. Pamiętam jak kilka lat temu zaliczałem matmę na inżynierze. Wtedy jeszcze chodziłem do Pana na korepetycje na ul. Reymonta dzięki temu zaliczyłem. A teraz dalej walczę z matematyką na magisterce i znowu potrzebuję pomocy. Pozdrawiam.
Nie ma sprawy, miło wspominam Reymonta, pozdrawiam!
Witam, Panie Krystianie.
Pani doktor u mnie na kolokwium nie uznała mi zadania policzonego Pańską metodą na pochodną kierunkową twierdząc, że nie zna takiego wzoru. Uznałaby mi to jeśli pokazałbym jej to w fachowej literaturze lub wytłumaczył co się skąd wzięło.
Czy ten wzór jest w jakiejś książce?
Czy pochodną kierunkową liczyć również tą metodą:
Pozdrawiam i dziękuję za to co Pan robi 🙂
Wzór jest wzięty po prostu z Krysickiego-Włodarskiego z rozdziału “Pochodne jednostronne i pochodne w kierunku osi” – u mnie tom II s.29, ale ja mam starsze wydanie.
W “oryginale” wzór wygląda tak:
{{\left( \frac{\partial f}{\partial s} \right)}_{0}}={{{f}’}_{x}}\left( {{x}_{0}},{{y}_{0}} \right)cos \alpha +{{{f}’}_{y}}\left( {{x}_{0}},{{y}_{0}} \right)cos \beta
gdzie: cos \alpha , cos \beta to cosinusy nachylenia wektora kierunkowego do osi układu współrzędnych. Pozwoliłem sobie zastąpić je współrzędnymi wektora kierunkowego (bo można) i dostałem “mój” wzór:
{{{f}’}_{{{{\vec{v}}}_{k}}}}\left( {{P}_{0}} \right)=\frac{\partial f}{\partial x}\left( {{P}_{0}} \right){{v}_{x}}+\frac{\partial f}{\partial y}\left( {{P}_{0}} \right){{v}_{y}}
Jest on oczywiście równoważny z wzorem wykorzystującym pojęcie gradientu, np: \frac{\partial f}{\partial {{{\vec{v}}}_{k}}}=\nabla f\circ {{\vec{v}}_{k}}
W Krysickim-Włodarskim bierze się on ze zdefiniowania pochodnej kierunkowej jako: {{\left( \frac{\partial f}{\partial s} \right)}_{0}}=\underset{t\to 0}{\mathop{lim }}\frac{f\left( {{x}_{0}}+tcos \alpha ,{{y}_{0}}+tcos \beta \right)-f\left( {{x}_{0}},{{y}_{0}} \right)}{t}, gdzie {{x}_{0}}+tcos \alpha , {{y}_{0}}+tcos \beta pochodzą z równania osi’ w kierunku której liczymy pochodną.
Jeśli weźniemy sobie funkcję złożoną:
F\left( t \right)=f\left( {{x}_{0}}+tcos \alpha ,{{y}_{0}}+tcos \beta \right)
…i potraktujemy jako funkcję złożoną jednej zmiennej, licząc jej pochodną (tak, jak pokazywałem to w Kursie Funkcji Wielu Zmiennych na Lekcji 4), wyjdziemy na nasz wzór (jeśli trzeba, mogę powolutku pokazać jak – ale bez definicji pochodnych cząstkowych jako takich się oczywiście nie obejdzie).
Stąd bierze się wzór.
Natomiast co do metody z linku to różni się od “mojej” tym, że do wskazania kierunku używa wektora, który NIE jest jednostkowy (a ja używam jednostkowych tylko). W myśl podanej przeze mnie i przez Krysickiego-Włodarskiego definicji był by to błąd (cosinusy kierunkowe nie są wtedy równe współrzędnym wektora), ale, jak pisze Wikipedia , jest to czasami dopuszczalne (przy przerobieniu definicji, oczywiście).
Mam nadzieję, że jakoś pomogłem, służę szczegółowym wyprowadzeniem wzoru z definicji, w razie czego.
Witam Panie Krystianie.
Ostatnio na egzaminie miałem takie zadanie: Oblicz pochodną kierunkową w punkcie P(3,4) f-cji f(x,y) = ln(x^2 + y^2)^1/2 w kierunku gradientu tej f-cji w tym punkcie. Szczerze mówiąc nie mam pojęcia jak się za to zabrać, mógłby Pan rozwiązać takie zadanie 🙂
Z góry dziękuje.
Witam,
Trzeba obliczyć gradient tej funkcji w tym punkcie, a potem jej pochodną w kierunku tego gradientu 🙂
Jedziemy:
f\left( x,y \right)=ln \sqrt{{{x}^{2}}+{{y}^{2}}}– jak rozumiem 🙂 ?
1. Liczę gradient ogólnie
Liczę, tak jak pokazałem w moim Kursie Całek Wielokrotnych :
gradf=\left[ \frac{\partial f}{\partial x},\frac{\partial f}{\partial y} \right]=\left[ \frac{1}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\frac{1}{2\sqrt{{{x}^{2}}+{{y}^{2}}}}2x,\frac{1}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\frac{1}{2\sqrt{{{x}^{2}}+{{y}^{2}}}}2y \right]=\left[ \frac{x}{{{x}^{2}}+{{y}^{2}}},\frac{y}{{{x}^{2}}+{{y}^{2}}} \right]
2. Liczę gradient w punkcie P(3,4)
gradf\left( 3,4 \right)=\left[ \frac{3}{{{3}^{2}}+{{4}^{2}}},\frac{4}{{{3}^{2}}+{{4}^{2}}} \right]=\left[ \frac{3}{25},\frac{4}{25} \right]
3. Liczę wektor kierunkowy do tego gradientu (pokazałem to w poście):
\left| \left[ \frac{3}{25},\frac{4}{25} \right] \right|=\sqrt{{{\left( \frac{3}{25} \right)}^{2}}+{{\left( \frac{4}{25} \right)}^{2}}}=\sqrt{\frac{25}{{{25}^{2}}}}=\sqrt{\frac{1}{25}}=\frac{1}{5}
{{\vec{v}}_{k}}=\frac{1}{\tfrac{1}{5}}\left[ \frac{3}{25},\frac{4}{25} \right]=\left[ \frac{3}{5},\frac{4}{5} \right]
4. Liczę pochodne cząstkowe funkcji w punkcie
Już je mam, bo liczyłem przy okazji liczenia gradientu w punkcie.
5. Podstawiam do wzoru:
{{{{f}’}}_{{{{\vec{v}}}_{k}}}}\left( P \right)=\frac{3}{25}\cdot \frac{3}{5}+\frac{4}{25}\cdot \frac{4}{5}=\frac{9}{125}+\frac{16}{125}=\frac{25}{125}=\frac{1}{5}
Koniec 🙂
x*dy/dx + y = xsinx jak obliczyc wartość takiego wyrażenia. Bardzo proszę o pomoc.
Chodzi o to, żeby rozwiązać to równanie różniczkowe?
Nie ma sprawy, to jest zupełnie standardowe równanie różniczkowe liniowe. Rozwiążę je metodą uzmienniania stałej, którą pokazałem i wytłumaczyłem dokładnie w moim Kursie Równań Różniczkowych.
xfrac{dy}{dx}+y=xsin x
xfrac{dy}{dx}+y=0
xfrac{dy}{dx}=-yquad /:xquad /cdot dxquad /:y
frac{dy}{y}=-frac{dx}{x}
ln left| y right|=-ln left| x right|+C
ln left| y right|=ln {{left| x right|}^{-1}}+Cquad /{{e}^{left( ldots right)}}
{{e}^{ln left| y right|}}={{e}^{ln {{left| x right|}^{-1}}+C}}
y={{e}^{ln{{left| x right|}^{-1}}}}{{e}^{c}}
y=Ccdot frac{1}{x}
y=frac{C}{x}
y=frac{Cleft( x right)}{x}
{y}’=frac{{C}’left( x right)x-Cleft( x right){x}’}{{{x}^{2}}}
{y}’=frac{{C}’left( x right)x-Cleft( x right)}{{{x}^{2}}}
xfrac{{C}’left( x right)x-Cleft( x right)}{{{x}^{2}}}+frac{Cleft( x right)}{x}=xsin x
frac{{C}’left( x right)x-Cleft( x right)}{x}+frac{Cleft( x right)}{x}=xsin x
frac{{C}’left( x right)x}{x}-frac{Cleft( x right)}{x}+frac{Cleft( x right)}{x}=xsin x
{C}’left( x right)=xsin x
Cleft( x right)=int{xsin xdx}
Cleft( x right)=sin x-xcos x+C
y=frac{sin x-xcos x+C}{x}
Panie Krzysztofie, a co jeśli nie mamy podanego punktu, a jedynie wektor? Jak rozwiązać taki przykład?
Trzeba zamiast współrzędnych punktu (liczb) wziąć zmienne x,y (a może i z, jeśli bawimy się w 3 wymiarach). Rozwiązaniem będzie jakaś ogólna funkcja dwóch zmiennych (albo trzech), ze zmiennymi x,y,(z), a nie konkretna liczba.
Dwa zadania ode mnie:
Obliczyć pochodną kierunkową funkcji f(x,y)=x^4 – 1/y w punkcie P(- 3^1/2, – 2) w kierunku prostej 1 + x*3^1/2 – y = 0
Oblicz pochodną kierunkową w kierunku gradientu: M(2-2;1) u=(x^2)+(y^2)+(z^2)
Za pomoc byłbym bardzo wdzięczny.
Proszę o pomoc 🙂
1. Oblicz pochodną kierunkową funkcji f (x,y)= ln(1+√(x^2+y^2) ) w punkcie (3,4) w kierunku wersora tworzącego kąt 45° z dodatnim kierunkiem osi OX. Dla jakiego wersora Ϭf/Ϭv (3,4) ma wartość największą?
Można to policzyć tak jak to Pan robił w przykładzie 3 czy można tutaj skorzystać z wzoru Ϭf/Ϭv(x,y)= Ϭf/Ϭx• cosα + Ϭf/Ϭy•sinα i wtedy wersor byłby ( √2/2,√2/2) ? I jak polczyć z tego wartość największą?
a co w wypadku gdy pytaja nas o wektor w kierunku którego przyrosty f(x,y) są NAJMNIEJSZE? jak podejść do tego?
Też tego szukałem.
Nie jestem pewien ale to będzie wektor prostopadły do gradientu funkcji.
Witam serdecznie.
Mam problem z zadaniem, gdzie wszystko jest podane, a wyliczyć trzeba wektor (wersor konkretnie). Mógłby Pan pokazać sposób na obliczenie tego.
(w tym przypadku moje zadanie brzmi “Wyznaczyć wersor V tak, aby pochodna w pkt (-1,1) fukncji f(x,y)=x^3 +ln(x^2 -x) w kierunku tego wektora była równa 0”).
Byłabym naprawdę wdzięczna za pomoc.
Pozdrawiam serdecznie 🙂
POMOCY> pochodne cząstkowe f(x,y)=x√(y²+1) -sin(xy)+3x^4y^4 oraz ekstremum lokalne dla f(x,y)=11-6x*8y-x²+y² bardzo proszę o pomoc:*
Pochodne cząstkowe funkcji
zostały obliczone w tym filmiku 🙂
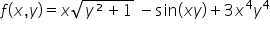
Ekstrema lokalne funkcji
zostały przedstawione tutaj:
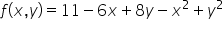
bardzo mi sie przydalo;D;D
super wyjasnienia;)
tyle ile ma pan cierpliwosci i checi to ja chyba nigdy nie bede mial :))) a co do zadan to perfekcyjnie wytlumaczone, po prostu teraz wszystko jasne
Dzięki, cieszę się, że się przydało.
Witam!
Panie Krystianie, świetnie rozumiem Pana sposób liczenia i nie mam problemów przy rozwiązywaniu zadań typu “Znajdź pochodną kierunkową funkcji: w punkcie P w kierunku od tego punktu do punktu Q.”
Problemy zaczynają się bowiem gdy pojawia się zadanie typu
“Oblicz pochodną kierunkową funkcji z=ln(x+y) w pkt. M(1,2) w kierunku stycznej poprowadzonej do paraboli y^2=4x ”
lub
“Pochodna kierunkowa f. z=y^2/x w kierunku prostej prostopadłej do stycznej elipsy 2x^2+y^2=1 w dowolnym punkcie” Nie bardzo wiem jak mogę użyć Pana metodę do tych zadań… Bardzo proszę o pomoc i schematyczny tok postępowania z wyżej wymienonymi zadaniami.
Nota Bene, jestem Pana wielkim fanem:)
Witam!
Zacytowane zadania to tylko cegła postawiona na fundamencie zadań typu “znajdź pochodną kierunkową od punktu P do Q”.
Wystarczy w nich wyznaczyć po prostu równanie rzeczonej stycznej (albo normalnej jak w drugim), obrać na niej dwa byle jakie punkty i mam już punkty P i Q.
Z tymi równaniami stycznych i normalnych to szło tak:
I. Jeżeli mamy funkcję w postaci jawnej y=f( x)i mamy wyznaczyć styczną/normalną w punkcie M(x_0,y_0) to:
Równanie stycznej: y-{{y}_{0}}={f}'( {{x}_{0}} )( x-{{x}_{0}})
Równanie normalnej (prostej prostopadłej do stycznej): x-{{x}_{0}}+{f}'( {{x}_{0}} )( y-{{y}_{0}} )=0
W Pan pierwszym przykładzie funkcję łatwo przerobić na postać jawną:
{{y}^{2}}=4x
y=2sqrt{x}quad vee quad y=-2sqrt{x}
Z czego wybieram y=2sqrt{x}, bo punkt M(1,2) należy do tej właśnie krzywej.
Czyli podstawiając do wzoru wyżej mam równanie stycznej:
y-2=frac{1}{2sqrt{1}}left( x-1 right)
y=frac{1}{2}x-frac{1}{2}+2
y=frac{1}{2}x+frac{3}{2}
(Wyznaczanie równań stycznej i normalnej w postaci jawnej pokazane jest także w moim Kursie Video: Kurs Pochodne Itd. )
Teraz biorę sobie dwa BYLE jakie punkty leżące na tej prostej (np. mogę sobie wziąść za x-sa zero i za x-sa 1 i w głowie “doliczyć” y-ki): (0,frac{3}{2}) , (1,2) i mam moje punkty P i Q. Dalej liczy Pan już według znanego schematu.
II. Jeżeli mam funkcję daną w postaci uwikłanej F(x,y)=0 i mamy policzyć styczną/normalną w punkcie M(x_0,y_0) , wzory są takie:
Na styczną: frac{partial F}{partial x}left( {{x}_{0}},{{y}_{0}} right)cdot left( x-{{x}_{0}} right)+frac{partial F}{partial y}left( {{x}_{0}},{{y}_{0}} right)cdot left( y-{{y}_{0}} right)=0
Na normalną: frac{partial F}{partial y}left( {{x}_{0}},{{y}_{0}} right)cdot left( x-{{x}_{0}} right)-frac{partial F}{partial x}left( {{x}_{0}},{{y}_{0}} right)cdot left( y-{{y}_{0}} right)=0
W Pana zadanie chodzi o “proste prostopadłe do stycznej”, czyli o normalne. Nie wyznacza się też tylko jednej z nich, tylko w ogóle całą ich pakę w dowolnym punkcie left( {{x}_{0}},{{y}_{0}} right).
Podstawiam więc co trzeba do wzoru na normalną:
2yleft( x-{{x}_{0}} right)-4xleft( y-{{y}_{0}} right)=0
Mam w ten sposób ogólne równanie normalnych w dowolnym punkcie elipsy left( {{x}_{0}},{{y}_{0}} right).
Teraz zadanie robi się trochę niefajne, bo nie wiadomo w sumie, w którym konkretnie punkcie liczyć tą pochodną kierunkową. Czy Panu profesorowi chodziło o to, żeby wybrać sobie samemu arbitralnie jakiś dowolny punkt, czy o to, żeby po prostu wyznaczyć ogólną rodzinę pochodnych kierunkowych jako funkcję punktów? Wynika to jakoś z treści zadania?
zdane na 3.5.Dziękuje serdecznie.Gdyby nie Pana pomoc i kursy to byłbym w d… 🙂
Nie ma sprawy, gratuluję!
Witam, wykładowca podał nam wzór aby liczyć pochodne kierunkowe, zupełnie inny aniżeli w/w. Wygląda on tak : lim t->0 = f(a + tp) – (a)/t
gdzie a – współrzędne punktu
p – współrzędne wektora;
Licząc pana sposobem i sposobem wykładowcy wyniki się różnią. Wolałabym jednak korzystać z pana wzoru, stąd moja prośba; czy mógłby się p. postarać się wyjaśnić różnicę. Z góry bardzo dziękuję 🙂
przepraszam, pomyłka we wzorze : lim t ->0 = f(a + tp) – f(a)/t
Witam
“Mój” wzór i Pani wzór to wzory równoważne. Czyli wyniki powinny wyjść takie same. Mój wzór wymaga różniczkowalności pochodnej w punkcie, ale to niuans i pewno nie na tym polega różnica.
Zgaduję że chodzi o to, że Pani wykładowca nie wymaga, aby wektor ‘p’ z Pani wzoru był wektorem jednostkowym, czy o to chodzi?
Jeśli tak, to na pewno tłumaczy to różnicę w wynikach.
Panie Krystianie jesczze jedno szybkie pytanko.Znajomi ze studiów zarzucaja mi ze z tych x i y powinno sie stworzyc kombinacje kazdy “x” z kazdym”y” i powinno byc P1(0,0) P2(0,-1/4)P3(-1/2,0)P4(-1/2,-1/4). Ja twierdez ze to jeden pieron bo tak naprawde potrzebujemy tutaj tylko X do sprawdzenia czy sa extrema wiec liczac te 4 punkty to tylko powielamy to samo( wystarczyłyby 2).Choc z drugiej strony pozniej przy podstawieniu pod funkcje wyszedłby nam inny wynik.ALe przeciez tez nie moze byc tak ze są 2 max. lokalne prawda ?:) kto ma racje ? i czy gdyby w tym zadaniu w macierzy powstałej z pochodnych II rzedu mielibysmy tez równiez gdzies y to wóczas trzebaby stworzyc 4 punkty podejrzane o ekstrema a wiec tak jak móia moi znajomi?
1. Nie powinno się tworzyć tych kombinacji, znajomi nie mają racji.
2. Jednak funkcja spokojnie może mieć nawet 20 ekstremów lokalnych. Niech Pan weźmie np. takie Tatry. Każdy czubek góry to było by maksimum lokalne i nie ma z tym większych problemów.
Naprawdę mocno polecam też mój Kurs Funkcje Wielu Zmiennych, tam spokojnie na obrazkach i przykładach tłumaczę te sprawy 🙂
Panie Krystianie skoro już jesteśmy przy pochodnych może będzie Pan w stanie mi pomóc w pewnym zadanku bo z wykładów nie wiele można wyciągnąć. Chodzi o :
Znajdź kierunek najszybszego wzrostu funkcji f(x,y,z)=(xy)^3+(y+z)^2 w pkt. A (1,1,1)
Tak, jasne, to nawet bardzo a’propos pytanie.
Kierunek najszybszego wzrostu funkcji w jakimś punkcie to po prostu wartość jej gradientu w tym punkcie (więcej o liczeniu gradientów jest w moim Kursie):
Czyli mając funkcję: [pmath]f(x,y,z)=(xy)^3+(y+z)^2[/pmath]
Liczymy jej pochodne cząstkowe:
[pmath]f_x{\prime}=3{(xy)^2}y[/pmath]
[pmath]f_y{\prime}=3{(xy)^2}x+2(y+z)[/pmath]
[pmath]f_z{\prime}=2(y+z)[/pmath]
Mamy więc gradient:
[pmath]grad(f)=delim{[}{3y(xy)^2,3x(xy)^2+2(y+z),2(y+z)}{]}[/pmath]
No i jego wartość w punkcie A(1,1,1), czyli konkretny, wybrany wektor z pola wektorowego:
[pmath]delim{[}{3*1(1*1)^2,3*1(1*1)^2+2(1+1),2(1+1)}{]}=delim{[}{3,5,2}{]}[/pmath]
Ten właśnie wektor wskazuje na kierunek najszybszego wzrostu funkcji (można jakoś \intuicyjne to zrozumieć, że w tym punkcie wartości funkcji zwiększają się “najszybciej” w tym samym kierunku, co ten wektor). Jeżeli na zajęciach tego wymagają, być może trzeba będzie jeszcze wyznaczyć z tego wektora kierunkowy do niego.
Dziękuję serdecznie mam jeszcze pytanie czy długość wektora przy 3 zmiennych liczy się analogicznie jak przy 2 zmiennych oraz czy przechodzi się na wektor kierunkowy w 3 zmiennych tak samo jak w dwóch? Pozdrawiam
Analogicznie 🙂
A nie powinno być [3,7,4] ? bo tam jest dodawanie np.: 2(1+1)
Panie Krystianie jeszcze jedno małe , szybkie pytanko bo znalazłem funkcje z któej wyliczałem tą pochodną :
f(x,y)=x^3+3xy-3y^2+1
Pochodne wyszły takie
fx=3x^2+3y
fy=3x-6y
Dobrze mi wyszło ?
Dobrze 🙂
Wielkie dzieki za pomoc! 🙂
a Od czego to zalezy , bo czesto ( jak nie zawsze) wychodziło nam na zajeciach 4 punkty podejrzane o ekstrema.Czemu np. w tym przypadku są 2 ?
Nie ma żadnej zasady, czasami w ogóle nie ma punktów podejrzanych o ekstrema, czasami jest jeden taki punkt, czasami więcej.
Taki akurat wyszedł układ równań z pochodnych cząstkowych, że miał dwa rozwiązania.
Powodzenia w weekend!
Czyli P1=0 a P2=-1/2 ?czy P1=0,0 a P2=-1/2,-1/4
[pmath]delim{|}{matrix{2}{2}{{6x} 3 3 {-6}}}{|}[/pmath] Wstawiam do tego za “x” i w pierwszej sytuacji wyjdzie mi -9 a w drugiej 9 ? Czyli ekstremum bedzie w P2 ? DObrze to zrobiłem ?
P1=(0,0), a P2=(-1/2.-1/4). Tak, dobrze Pan zrobił, o to chodzi. Ekstremum będzie w P2.
Błagam , bo nie wiem jak to ma wyglądac w wypadku gdy wulicza sie tylko dla X a w weekend mam poprawe z matematyki 🙁
Pochodne wyszły takie:
[pmath]f_x{\prime}=3x^2+3y[/pmath]
[pmath]f_y{\prime}=3x-6y[/pmath]
prawda?
Teraz trzeba utworzyć układ równań:
[pmath]3x^2+3y=0[/pmath]
[pmath]3x-6y=0[/pmath]
Wyznaczyć np. y z pierwszego równania:
[pmath]3y=-3x^2[/pmath] /:3
[pmath]y=-x^2[/pmath]
Wstawić do drugiego równania:
[pmath]3x-6(~-x^2)=0[/pmath]
[pmath]3x+6x^2=0[/pmath]
[pmath]3x(1+2x)=0[/pmath]
[pmath]x=0[/pmath] lub [pmath]1+2x=0[/pmath]
[pmath]x=0[/pmath] lub [pmath]2x=-1[/pmath]
[pmath]x=0[/pmath] lub [pmath]x=-1/2[/pmath]
I mamy wyznaczone współrzędne x-sowe punktów podejrzanych o to, że mogą być ekstremami – czy o to chodziło? To właśnie te współrzędne trzeba będzie wstawić w II etapie zadania za ‘x’ w wyrażeniu ‘6x’ (oczywiście trzeba jeszcze do nich doliczyć współrzędne y-kowe ze wzoru: [pmath]y=-x^2[/pmath]). Wyjdą dwa punkty podejrzane o bycie ekstremami.
Chodzi mi o przyrównanie do 0.Jak to wyliczyc ?
a jak włąsnie wyliczyc tego x ?:)
Nie wylicza się, tylko za ‘x’ wstawia współrzędne x-sowe punktu podejrzanego o nieciągłość.
Wrzucę może cały schemat, jak to się robi (pokazuję też to dokładnie w swoim Kursie):
Schemat obliczania ekstremów lokalnych funkcji 2 zmiennych
a jak teraz bedzie wyglądac wyliczenie 4 punktów podejrzanych o ekstrema ?:)
Współrzędne każde z nich wrzucasz po kolei do wyznacznika:
[pmath]delim{|}{matrix{2}{2}{{6x} 3 3 {-6}}}{|}[/pmath] (oczywiście w tym przypadku tylko ich wspórzędną x-ową w elemencie 6x) i orientujesz się, jaki wyjdzie znak wyznacznika 🙂
witam.Mam pytanie czy przy wyliczeniu ekstremó lokalnych ( niestety nie pamietam funckcji) pochodne drugiego rzedu moga wyjsc takie :
fxx=6x fxy=3
fyx=3 fyy=-6
Chodzi mi o to ze nie otrzymalismy nic z “y” Czy tak moze byc ?
Pochodne wynosiły:
fx=3x^2+3y
fy=3x-6y
Mogą wyjść i może tak być, nie ma problemu 🙂
Mam prośbę! Czy mógłby Pan pokazać jak zrobić takie zadanie ale z 3 zmiennymi?
I najlepiej jakby to było jakieś zadanie, w którym podany jest kąt, a nie wektor.
Jasne. W przypadku 3 zmiennych mamy daną funkcję:
[pmath]f(x,y,z)[/pmath], punkt [pmath]P_0[/pmath] i wektor [pmath]\vec{v}[/pmath].
Wzór na pochodną kierunkową z funkcji [pmath]f[/pmath], w punkcie [pmath]P_0[/pmath] w kierunku wektora [pmath]\vec{v}[/pmath] przyjmuje postać (dodajemy po prostu jedną zmienną):
[pmath]f{\prime}_{\vec{v}_k}(P_0)={{\partial}f}/{{\partial}x}(P_0)*v_x+{{\partial}f}/{{\partial}y}(P_0)*v_y+{{\partial}f}/{{\partial}z}(P_0)*v_z[/pmath]
Współrzędne [pmath]v_x,v_y,v_z[/pmath] to NIE są współrzędne wektora [pmath]\vec{v}[/pmath], tylko jego wektora kierunkowego [pmath]\vec{v}_k[/pmath], co pokazywałem w poście wyżej.
Opcjonalnie zamiast wektora kierunek może wyznaczać oś OS o zadanych kątach nachylenia do osi układu współrzędnych OX, OY i OZ. Mamy wtedy dane: [pmath]f(x,y,z)[/pmath], punkt [pmath]P_0[/pmath] i trzy kąty nachylenia do osi (powiedzmy [pmath]alpha[/pmath] do osi OX, [pmath]beta[/pmath] do osi OY, [pmath]gamma[/pmath] do osi OZ). Zamiast kątów możemy też mieć dane np. ich cosinusy, a to nawet lepiej, bo wtedy wzór na pochodną kierunkową przyjmuje postać:
[pmath]f{\prime}_{OS}(P_0)={{\partial}f}/{{\partial}x}(P_0)*cos{\alpha}+{{\partial}f}/{{\partial}y}(P_0)*cos{beta}+{{\partial}f}/{{\partial}z}(P_0)*cos{gamma}[/pmath]
, no a cosinusy z danych kątów liczy się chyba łatwiej, niż współrzędne wektora kierunkowego z danego wektora.
Przykład
Oblicz pochodną z funkcji [pmath]f(x,y,z)=x^2+y^3+2z[/pmath] w punkcie [pmath](1,0,-2)[/pmath] w kierunku osi OS, której kąty nachylenia do osi układu współrzędnych wynoszą: do osi OX [pmath]45^0[/pmath], do osi OY [pmath]60^0[/pmath], do osi OZ [pmath]90^0[/pmath].
Przypomnijmy ogólny wzór:
[pmath]f{\prime}_{OS}(P_0)={{\partial}f}/{{\partial}x}(P_0)*cos{\alpha}+{{\partial}f}/{{\partial}y}(P_0)*cos{beta}+{{\partial}f}/{{\partial}z}(P_0)*cos{gamma}[/pmath]
Wstawiamy do niego wszystko z marszu, licząc w pamięci pochodne:
[pmath]f{\prime}_{OS}(P_0)=2*1*cos45^0+3*{0^2}*cos60^0+2*cos90^0=2*{{\sqrt{2}}/2}+0+0=\sqrt{2}[/pmath]
KONIEC
Dziękuję ;))
To moźe by Pan panie Krystianie poprawił, jeśli jest taka możliwość swoje przeoczenie, bo wprowadza to niepotrzeby zamęt.
Poprawiłem, przepraszam!
Podobnie w przykładzie 3 – podstawia pan 2,1 zamiast zapowiedzianego w poleceniu 1,2. A swoją drogą, baaaardzo przydatny wpis, zwiększa szanse na zdanie egzaminu, bardzo dziekuję za zamieszczenie 🙂
Tak ,ma Pan rację w obu przypadkach (Przykład 1 i Przykład 3) z niewiadomych dla mnie przyczyn nie wstawiłem właściwych współrzędnych punktów, co rozwaliło cały wynik.
Przepraszam!
Witam, czy w pierwszym przykładzie do pochodnych cząstkowych nie powinno się podstawić wartości punktu P czyli 1 i 2 a nie, tak jak Pan zrobił, 3 i -1 ?
a jak obliczyć pochodną kierunkową 2 rzędu, np.taki przykład f(x,y)=y2-e(do potęgi x) , Po=(!,2) u=[1,-1]