Mój nowy Kurs – pochodne funkcji i ich zastosowania
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Dzisiaj podpiąłem do sprzedaży mój Kurs Pochodnych – możesz kliknąć na link na prawym pasku i zobaczyć, co i jak.
Materiału video jest w nim około 10 godzin, tak więc jest co ćwiczyć. Pochodne jak to pochodne, podstawa to nauczyć się je liczyć naprawdę dobrze, a potem wszystko leci już z górki.
Przy samej nauce pochodnych łatwo złapać kilka niedobrych manier, które starałem się zwalczać w Kursie.
Do Kursu dodane jest też liczenie granic w ramach reguły de l’Hospitala – bo wykorzystuje ona właśnie pochodne funkcji, a także obliczanie dziedziny funkcji, niezbędne do zbadania jej zmienności.
Polecam i mam nadzieję, że Kurs się Wam przyda.
Jedna z wielu opinii o naszych Kursach...
Świetny kurs, zagadnienia wytłumaczone w bardzo przystępny sposób. Niech o jego jakości świadczy fakt, że po jednorazowym wysłuchaniu i zrobieniu wszystkich zadań zdałam statystykę, z której miałam już dwa razy warunek.Ewelina
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
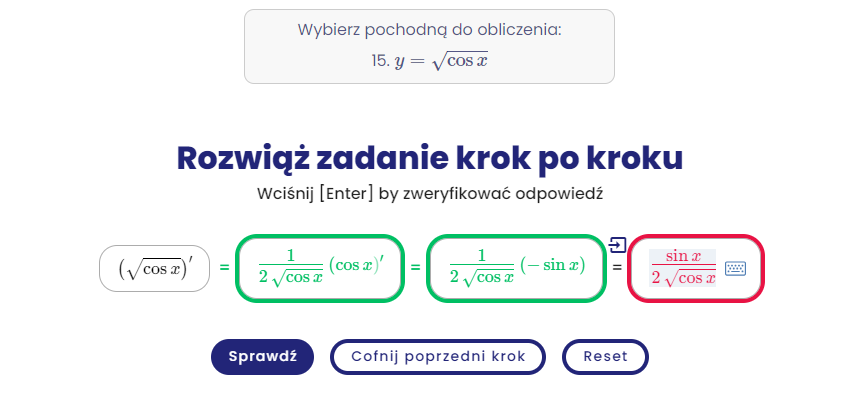
Pls o pomoc! Nie wiem gdzie dokładnie zakwalifikować moje pytanie, ale z góry dziękuję za odpowiedź. Zadanie niby łatwe, ale nie jestem pewna co do punktu styczności.Zadanie:Dana jest funkcja y= 6lnx. Znajdź tangens kąta pod jakim przecina ona oś x.Wiem, że tg
=f'(
), ale wiem czy, na pewno 
= 1
a ja siedzialem i liczylem ten przyklad z godzine a tu prosze 🙂
No właśnie coś mi tu nie pasowało 🙂 Dziękuję za odpowiedź.
Źle ułożyłem ten przykład w Zadaniu Domowym:
17)
To nie jest w ogóle symbol nieoznaczony!
Zainteresowanych bardzo przepraszam za pomyłkę.
Nie bardzo rozumiem skąd wziął się wynik w zadaniu 17 z De L’Hospitala.