Mój nowy filmik video jest odpowiedzią na pytanie p. Marcina w komentarzach.
Pokazuję na nim, jak zbadać monotoniczność funkcji f\left( x \right)={{\left( x-2 \right)}^{5}}{{\left( 2x+1 \right)}^{4}} i jak ważne – w tym konkretnym przykładzie – było umiejętne uporządkowanie wyniku. Przy okazji mała powtórka ze szkoły średniej i nierówności wielomianowych.
Przykład- jak powiedziałem w filmiku – dosyć nietypowy, ale się zdarza.
Tutaj jeszcze link do tej funkcji w WolframAlpha (omawiam go na końcu filmiku):
Oraz do mojego darmowego Praktycznego Przewodnika do WolframAlpha, gdzie pokazuję, jak pomagać sobie nim do przykładów, które masz na studiach:
WolframAlpha Praktyczny Przewodnik
Jeśli masz jakieś pytania – zadaj je śmiało w komentarzach pod postem.

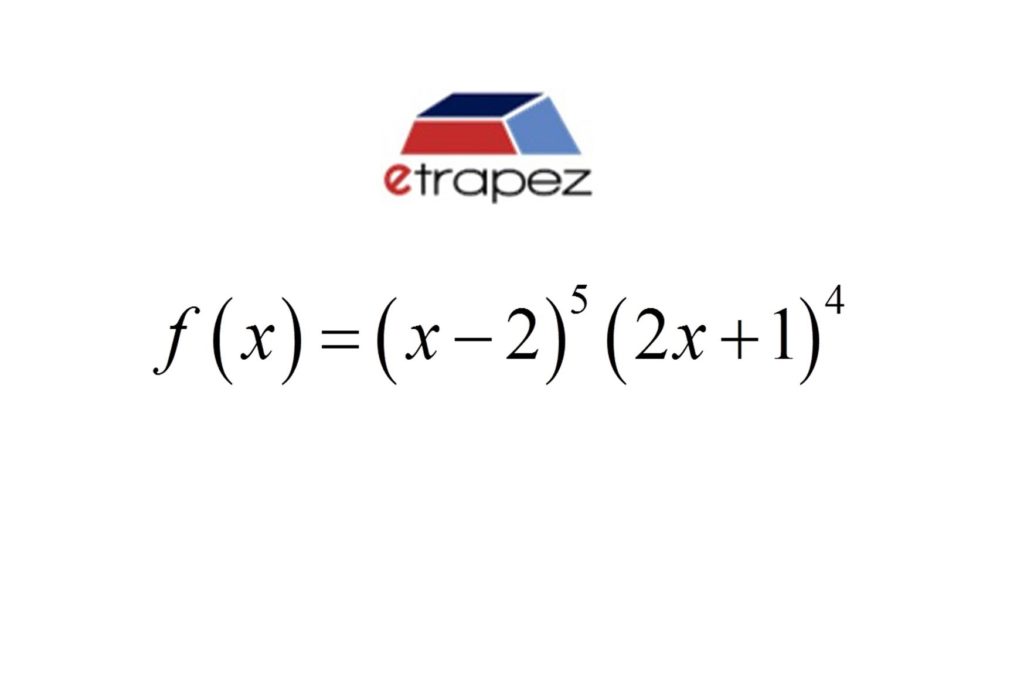

15 Komentarzy
Konrad
Witam,mam problem z rozwiązaniem zadania tego typu Po obliczeniu pochodnej, nie wiem co dalej zrobić.
Po obliczeniu pochodnej, nie wiem co dalej zrobić.
Madzia
Witam! czy w przykładzie 7 (zadanie domowe) jest blad? delta wynosi u mnie zero a według odpowiedzi powinna wyjść na minusie ?
Mariusz
Jeśli pochodna rośnie to funkcja jest wypukła
Jeśli pochodna maleje to funkcja jest wklęsła
ale to już inna bajka
Rafał
Witam!!
Mam problem z jedną sprawą, mam przykład xe^(1/x), w kursie jest że, gdy mianownik jest lub może być ujemny to nie mnożymy przez niego(kiedy przyrównuję pochodną do 0), na tym się zatrzymałem, a jak mimo to pomnożę to źle mi wychodzi
Krystian Karczyński
Witam!
Tak, dokładnie, to jest przykład, w którym można wpaść w pułapkę. Rozwiązuję krok po kroku:
y=x{{e}^{tfrac{1}{x}}}
Dy:xin Rbackslash \{ 0 }
{y}'={{left( x{{e}^{tfrac{1}{x}}} right)}^{prime }}={{left( x right)}^{prime }}{{e}^{tfrac{1}{x}}}+x{{left( {{e}^{tfrac{1}{x}}} right)}^{prime }}={{e}^{tfrac{1}{x}}}+x{{e}^{tfrac{1}{x}}}{{left( frac{1}{x} right)}^{prime }}={{e}^{tfrac{1}{x}}}+x{{e}^{tfrac{1}{x}}}left( -frac{1}{{{x}^{2}}} right)=
={{e}^{tfrac{1}{x}}}-frac{{{e}^{tfrac{1}{x}}}}{x}={{e}^{tfrac{1}{x}}}left( 1-frac{1}{x} right)
D{y}':xin Rbackslash \{ 0 }
{{e}^{tfrac{1}{x}}}left( 1-frac{1}{x} right)=0quad /:{{e}^{tfrac{1}{x}}}– możemy podzielić przez {{e}^{tfrac{1}{x}}}, bo {{e}^{tfrac{1}{x}}}jest zawsze dodatnie
1-frac{1}{x}=0
Tutaj jest ważny i krytyczny moment. NIE możemypomnożyć obustronnie przez x, ponieważ xprzyjmuje wartości albo dodatnie, albo ujemne. Czyli musimy zrobić tak:
1-frac{1}{x}=0quad /cdot {{x}^{2}}– możemy pomnożyć przez x^2, bo x^2jest zawsze dodatnie (w naszej dziedzinie funkcji).
{{x}^{2}}-x=0
xleft( x-1 right)=0
x=0quad vee quad x=1
Albo tak:
1-frac{1}{x}=0
frac{x}{x}-frac{1}{x}=0
frac{x-1}{x}=0
xleft( x-1 right)=0
x=0quad vee quad x=1
Teraz możemy narysować przybliżony wykres, według reguł podanych w Kursie:
No i napisać odpowiedź:
Odp. Funkcja y=x{{e}^{tfrac{1}{x}}}jest rosnąca dla xin left( -infty ,0 right)cup leftlangle {} right. 1,infty ),malejąca dla xin (, 0,1 rangle, osiąga minimum dla x=1.
{{y}_{min }}left( 1 right)=1cdot {{e}^{tfrac{1}{1}}}=e
Co potwierdza wykres funkcji y=x{{e}^{tfrac{1}{x}}}:
Tomasz
Wszystko się wyjaśniło. Tempo zmienności funkcji pokazane jest w tym temacie.
Tomasz
Witam, nurtuje mnie pewna kwestia.
Jak odczytać, lub wyliczyć przedział w którym funkcja rośnie coraz szybciej, rośnie coraz wolniej, maleje coraz szybciej, maleje coraz wolniej?
Pozdrawiam
Krystian Karczyński
Witam, dobre pytanie.
Trzeba policzyć jej pochodną. Im pochodna jest większa, tym funkcja rośnie „szybciej”
Omówiłem to w tym wykładziku, zapraszam.
Tomasz
Dzięki za odpowiedź.
Wiem, że:
f ’ (x) > 0
f ” (x) > 0
to funkcja rośnie coraz szybciej.
f ’ (x) > 0
f ” (x) < 0
to funkcja rośnie coraz wolniej.
f ' (x) < 0
f '' (x) < 0
to funkcja maleje coraz szybciej.
f ' (x) 0
to funkcja maleje zoraz wolniej.
Tyle z teorii, nie wiem jak wyznaczyć przedziały, w których dana funkcja właśnie rośnie coraz szybciej itd.
Czy można liczyć na jakiś poradnik video związany z tempem zmian wartości funkcji?
Tomasz
W ostatnim wdarły się błędy, chodzi o.
f ’ (x) 0
to funkcja maleje coraz szybciej.
Tomasz
Coś nie chce dobrze tego przedstawić, ale wie Pan o co chodzi. Da się te przedziały jakoś w miarę prosto odczytać lub obliczyć?
Marcin
Witam Panie Krystianie, czy byłby Pan w stanie zrobić video, gdzie od deski do deski wyjaśnione jest badanie przebiegu zmienności funkcji według punktów w schemacie, z tabelką, wykresem etc, na przykładzie takiej oto np nieskomplikowanej funkcji: y=(x^+1)/(x^2-4)
Pozdrawiam, Marcin.
Krystian Karczyński
Na pewno, tylko takie badanie naprawdę długo trwa, myślę, że co najmniej 40 minut… Jakby co, to zapraszam do mojego Kursu, gdzie jest ono zawarte (oczywiście nie dokładnie na tym przykładzie):
https://etrapez.pl/produkt/kurs-pochodne-i-badanie-przebiegu-zmiennosci-funkcji/
Ania
Uwielbiam pana kursy!
Nie myślał pan o zrobieniu kursu z Badań operacyjnych?
Pozdrawiam
Piotr
Kursy super , proponuje wydać książkę napisaną właśnie językiem potocznym 😀 , (oczywiście w granicach rozsądku) bo czasem naprawdę brakuje pod ręką dobrego poradnika matematycznego, żeby sobie szybko coś powtórzyć. (i nie siedzieć całego dnia przed komputerem)
Pozdrawiam