Pochodne Funkcji Wykład 3
Temat: Pochodne jednostronne. Pochodne nieskończone.
Streszczenie
Na wykładzie pokażę, czym są pochodne jednostronne funkcji, a także jej pochodne nieskończone. Zobaczymy też, jak wykazać, że pochodna funkcji nie istnieje.
Pochodne jednostronne funkcji
Definiując pochodne (niezależnie od tego, czy w sposób opisany w Wykładzie 1, czy w Wykładzie 2) doszliśmy do tego, że pochodna funkcji w punkcie ![]() jest pewnego rodzaju granicą funkcji:
jest pewnego rodzaju granicą funkcji:
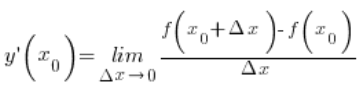
Granicę tą uzyskaliśmy…
1. Na pierwszym wykładzie obliczając coraz bardziej precyzyjne prędkości średnich dla przyrostów czasu coraz bliższych ![]() . Na przykładzie w wykładzie były to prędkości średnie między 2 a 2,5 sekundą ruchu, potem między 2 a 2,25 sekundą, między 2 a 2,1 sekundą itd. Nasze
. Na przykładzie w wykładzie były to prędkości średnie między 2 a 2,5 sekundą ruchu, potem między 2 a 2,25 sekundą, między 2 a 2,1 sekundą itd. Nasze ![]() zwiększaliśmy więc o przyrosty
zwiększaliśmy więc o przyrosty ![]() i dążyliśmy z tymi przyrostami do zera. Nic nie stało na przeszkodzie, abyśmy brali prędkości średnie pomiędzy 1,5 a 2 sekundą, 1,75 a 2 sekundą, 1,9 a 2 sekundą itd, a więc zmniejszali byśmy o przyrosty
i dążyliśmy z tymi przyrostami do zera. Nic nie stało na przeszkodzie, abyśmy brali prędkości średnie pomiędzy 1,5 a 2 sekundą, 1,75 a 2 sekundą, 1,9 a 2 sekundą itd, a więc zmniejszali byśmy o przyrosty ![]() i dążyli z tymi przyrostami do zera.
i dążyli z tymi przyrostami do zera.
Pochodną uzyskaną wyniku dążenia do ![]() z prawej strony możemy nazwać pochodną prawostronną funkcji i oznaczyć ją:
z prawej strony możemy nazwać pochodną prawostronną funkcji i oznaczyć ją:
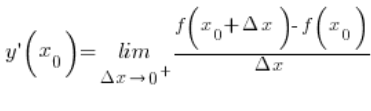
Pochodną uzyskaną wyniku dążenia do ![]() z lewej strony możemy nazwać pochodną lewostronną funkcji i oznaczyć ją:
z lewej strony możemy nazwać pochodną lewostronną funkcji i oznaczyć ją:
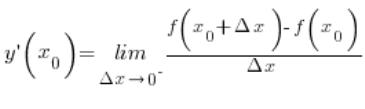
W naszym przykładzie z Kaziem na sankach obie te pochodne wyszły by równe (gorąco, gorąco, gorąco polecam wyciągnąć kalkulator i to sprawdzić, obliczając kolejne prędkości średnie). Nie jest to jednak regułą we wszystkich funkcjach i we wszystkich pochodnych. Czasami podchodząc do ![]() z prawej strony uzyskamy inny wynik (granicę), niż z lewej. Czasami możemy podchodzić tylko z którejś strony, bo po drugiej w ogóle funkcji nie ma… Może być różnie.
z prawej strony uzyskamy inny wynik (granicę), niż z lewej. Czasami możemy podchodzić tylko z którejś strony, bo po drugiej w ogóle funkcji nie ma… Może być różnie.
2. Na drugim przykładzie doszliśmy do pochodnej biorąc kolejne sieczne: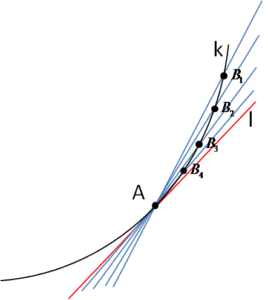 Zauważ, że na naszym przykładzie definiując styczną brałem punkty
Zauważ, że na naszym przykładzie definiując styczną brałem punkty ![]() , czyli punkty zbliżające się do A z prawej strony. Umawiając się, że biorę tylko takie punkty uzyskam przyrosty argumentów
, czyli punkty zbliżające się do A z prawej strony. Umawiając się, że biorę tylko takie punkty uzyskam przyrosty argumentów ![]() dodatnie, a wzór na tangens kąta nachylenia stycznej:
dodatnie, a wzór na tangens kąta nachylenia stycznej:
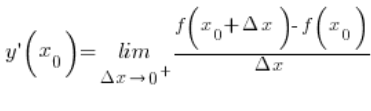
Równie dobrze jednak mogłem brać te punkty na krzywej dążące do A z lewej strony – w tym przypadku przyrosty ![]() będą ujemne, a wzór na odpowiedni tangens:
będą ujemne, a wzór na odpowiedni tangens:
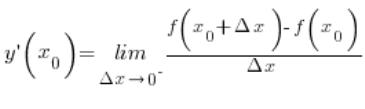
Biorąc sieczne z lewej lub z prawej strony uzyskamy tą samą (albo i nie) styczną. Mówimy więc o stycznej lewostronnej i stycznej prawostronnej. Mogą to być, w przypadku niektórych funkcji, dwie różne proste, które mają różne tangensy kąta nachylenia do osi OX.
Pojęcie pochodnych jednostronnych wynika więc nawet dosyć naturalnie z samego intuicyjnego rozumienia tego, czym są pochodne. Jeżeli jednak nawet znalibyśmy tylko i wyłącznie samą definicję granicy funkcji w punkcie ![]() :
:
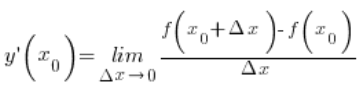
to pamiętając z Wykładów o samych granicach funkcji, że granica może być lewo i prawostronna, że istnieje wtedy, kiedy lewo i prawostronne są równe itd.
Po prostu zapominając na chwilę o tym, że jest to pochodna i zostając tylko i wyłącznie na gruncie granic funkcji obliczymy i zrozumiemy wszystko, co jest nam potrzebne z granic jednostronnych.
Pochodne jednostronne – kiedy ich używać?
Po zapoznaniu się z powyższym budzi się na pewno w każdym studencie pewien swoisty lęk – co to są pochodne to już jako tako umiem, liczyć jakoś tam umiem, wzory niby mam i teraz aby nauczyć się pochodnych muszę umieć JESZCZE COŚ NOWEGO?
Spokojnie. W praktycznych obliczeniach na studiach w 99% przypadków będziesz miał sytuację, w której pochodna lewo i prawostronna funkcji są sobie równe, a w tym przypadku w ogóle nie ma co wprowadzać analizy lewo i prawostronnej zachowania się granicy. Pochodna z ![]() to jest po prostu w każdym punkcie
to jest po prostu w każdym punkcie ![]() , nie ma tu w ogóle potrzeby nawet znajomości tych subtelnych rozróżnień.
, nie ma tu w ogóle potrzeby nawet znajomości tych subtelnych rozróżnień.
Pochodne jednostronne mogą Ci się jednak przydać do dwóch rzeczy:
- Do lepszego rozumienia tego, czym są pochodne (nie lekceważyłbym tej sprawy)
- Do rozwiązywania pewnego rodzaju szczególnych zadań, na przykład na sprawdzanie, czy pochodna w punkcie istnieje (a będzie istnieć, gdy pochodne lewo i prawostronna są równe)
- Do trudniejszych analiz ogólnie
Szkolnym przykładem na punkt 2. jest:
Przykład
Sprawdź, czy funkcja ![]() ma pochodną w punkcie
ma pochodną w punkcie ![]() .
.
Funkcja ![]() narysowana w układzie współrzędnych wyglądała by tak:
narysowana w układzie współrzędnych wyglądała by tak:
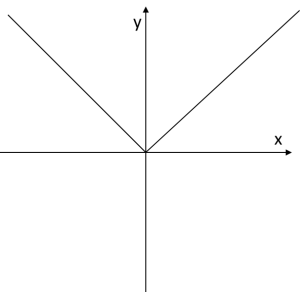 Pytanie jest – czy ma on pochodną w punkcie
Pytanie jest – czy ma on pochodną w punkcie ![]() ? Niby w sumie – czemu nie? No ale przyjrzyjmy się bliżej. Liczymy granicę prawostronną:
? Niby w sumie – czemu nie? No ale przyjrzyjmy się bliżej. Liczymy granicę prawostronną:
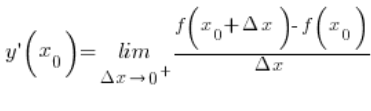
Biorą za ![]() :
:
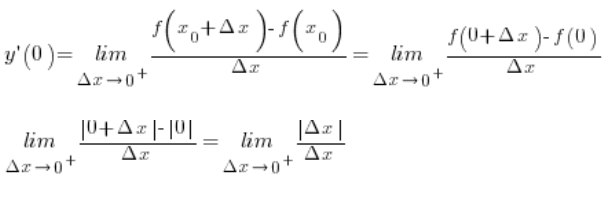
Teraz ważny moment. ![]() jest dodatnie (wiemy to stąd, że liczymy granicę przy
jest dodatnie (wiemy to stąd, że liczymy granicę przy 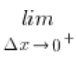 ), a wartości bezwzględna z liczby dodatniej jest równa tej liczbie, zatem:
), a wartości bezwzględna z liczby dodatniej jest równa tej liczbie, zatem:
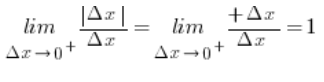
Pochodna prawostronna jest więc równa 1.
Liczymy granicę lewostronną:
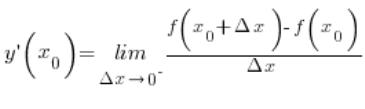
Biorą za ![]() :
:
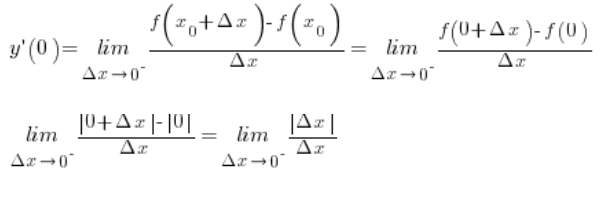
Teraz znowu ważny moment. ![]() jest ujemne (wiemy to stąd, że liczymy granicę przy
jest ujemne (wiemy to stąd, że liczymy granicę przy 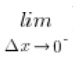 ), a wartości bezwzględna z liczby dodatniej jest równa tej liczbie z minusem (całość musi być dodatnia), zatem:
), a wartości bezwzględna z liczby dodatniej jest równa tej liczbie z minusem (całość musi być dodatnia), zatem:
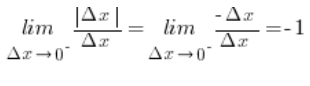
Pochodna lewostronna jest więc równa -1.
Zatem pochodna lewo i prawostronna są różne od siebie. Morał z tego taki, że pochodna z funkcji ![]() w punkcie
w punkcie ![]() nie istnieje.
nie istnieje.
Pochodne nieskończone
Skoro – jak już wiemy – pochodna funkcji w punkcie to pewna granica, nic nie stoi na przeszkodzie, aby dążyła ona do ![]() lub
lub ![]() – jak każda porządna granica. Tak uzyskaną pochodną możemy nazwać pochodną nieskończoną. Oczywiście możemy mówić też o pochodnej lewostronnej i prawostronnej nieskończonej (tak jak w przypadku każdej granicy). Interpretacją geometryczną takiej granicy są sieczne dążące do stycznej pionowej (tangens
– jak każda porządna granica. Tak uzyskaną pochodną możemy nazwać pochodną nieskończoną. Oczywiście możemy mówić też o pochodnej lewostronnej i prawostronnej nieskończonej (tak jak w przypadku każdej granicy). Interpretacją geometryczną takiej granicy są sieczne dążące do stycznej pionowej (tangens ![]() dąży do
dąży do ![]() lub
lub ![]() ).
).
Przykład
Oblicz pochodną funkcji ![]() w punkcie
w punkcie ![]() .
.
Mamy więc obliczyć:
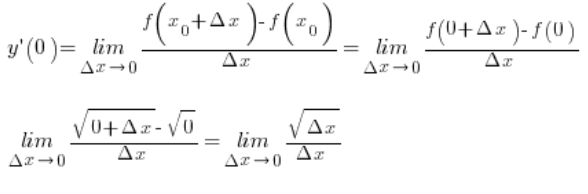
W tym przypadku nie ma sensu liczyć pochodnej lewostronnej przy ![]() . Nie możemy brać
. Nie możemy brać ![]() ujemnych, bo pierwiastki (rzeczywiste, ale nie motajmy) z liczb ujemnych nie istnieją. Jeśli więc istnieje pochodna w tym punkcie to tylko prawostronna, mamy więc:
ujemnych, bo pierwiastki (rzeczywiste, ale nie motajmy) z liczb ujemnych nie istnieją. Jeśli więc istnieje pochodna w tym punkcie to tylko prawostronna, mamy więc:
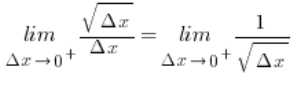
Co dąży do plus lub minus nieskończoności (granice funkcji się kłaniają, symbol ![]() ), a skoro mianownik i licznik są dodatnie, to do plus nieskończoności.
), a skoro mianownik i licznik są dodatnie, to do plus nieskończoności.
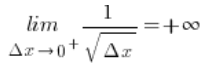
Zatem funkcja ![]() ma w punkcie
ma w punkcie ![]() pochodną prawostronną równą
pochodną prawostronną równą ![]() .
.
Rysując wykres funkcji ![]() i biorąc kolejne sieczne…
i biorąc kolejne sieczne…
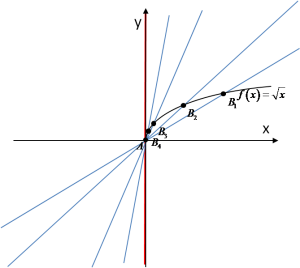
…widzimy, że graniczną prostą dla tych siecznych jest prosta pionowa, o kącie nachylenia do osi OX ![]() .
.
KONIEC
Pisząc tego posta korzystałem z…
1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.
Kliknij, aby przypomnieć sobie, jak zinterpretować pochodną jako tangens (poprzedni Wykład) <–


“Morał z tego taki, że pochodna z funkcji ma pochodną w punkcie nie istnieje. “Czy nie powinno być raczej : ” (…) że pochodna z funkcji w punkcie nie istnieje. “ Pozdrawiam
Tak, tak powinno dokładnie być. Poprawiłem i dziękuję.
Dobre, latwostrawne.
PS “Piszac ten post”, a nie “tego posta” 🙂