
Rząd macierzy szacowany „na oko”
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Definicja rzędu macierzy i co z niej wynika
Załóżmy, że zdefiniowaliśmy rząd macierzy jako: „liczba liniowo niezależnych wierszy i kolumn w macierzy”. Jakie już „na starcie” właściwości rzędów wynikają z tej definicji?
Po pierwsze, oczywiste jest, że rząd macierzy może być równy: 1, albo 4, albo czasami 0. Ale na pewno nie wyjdzie równy: -4, czy ![]() .
.
No dobra, to wszystko, co z niej wynika?
Ale czy to wszystko, co można wycisnąć? Weźmy na przykład macierz:
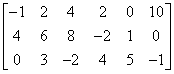
Ta macierz ma 3 wiersze i 6 kolumn.
Zadajmy sobie pytanie, jaki może być rząd tej macierzy? Czy może nam wyjść równy 7? Chyba jest jasne, że nie, bo skoro rząd macierzy to „liczba liniowo niezależnych wierszy i kolumn”, nie możę w tym przypadku być równy 7, bo ta macierz nie ma w ogóle ani tyle wierszy, ani tyle kolumn!
A teraz trudniejsze pytanie… Czy rząd może być równy 6? Macierz ma przecież 6 kolumn…
Odpowiedź brzmi: nie. 6 musiało by być „liczbą liniowo niezależnych wierszy i kolumn”. 6 może być liczbą liniowo niezależnych kolumn (bo ich jest 6), ale nie może być liczbą liniowo niezależnych wierszy (bo jest ich tylko 3). A powinno być liczbą liniowo niezależnych „wierszy i kolumn”.
Oczywiste jest więc, że rząd tej macierzy może wyjść maksymalnie 3.
Dochodzimy tu do pożytecznej własności:
![]()
Patrząc więc na macierz, od razu można powiedzieć, ile wyniesie jej rząd maksymalnie – co czasami bywa bardzo użyteczne.
Aby policzyć go dokładniej, potrzebujesz już jednak zastosować odpowiednie metody – pokazuję je w moim Kursie poświęconym macierzy na Lekcji 5, zapraszam!
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.









