जटिल बहुपदीय समीकरणों का समाधान करते समय, हम आमतौर पर वही विधियां इस्तेमाल करते हैं जैसे कि हम हाई स्कूल में वास्तविक बहुपदीय समीकरणों को हल करने के लिए करते हैं।
दूसरे डिग्री में कमी योग्य चौथे डिग्री के जटिल समीकरण
यह उन चौथे डिग्री के जटिल समीकरणों पर भी लागू होता है जिन्हें दूसरे डिग्री के समीकरणों में कम किया जा सकता है, यानि वे जिनमें चर चौथे घात, दूसरे घात और एक स्वतंत्र पद होते हैं, उदाहरण के लिए:
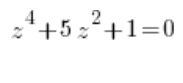
या:
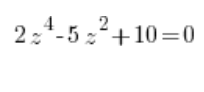
हम इस प्रकार की जटिल समीकरणों को दूसरी डिग्री की जटिल समीकरणों में परिवर्तित करते हैं जिसमें ![]() का प्रयोग करते हैं, जहाँ
का प्रयोग करते हैं, जहाँ ![]() स्पष्ट रूप से जटिल चर है।
स्पष्ट रूप से जटिल चर है।
कार्य
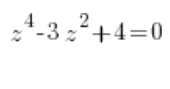
हम ![]() (बिल्कुल
(बिल्कुल 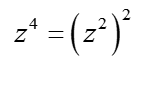 ) का प्रयोग करते हैं, इस प्रकार हमें मिलता है:
) का प्रयोग करते हैं, इस प्रकार हमें मिलता है:
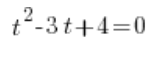
और इस प्रकार हम इस समीकरण को सामान्य तरीके से डेल्टा का उपयोग करके हल करते हैं (बेशक, नकारात्मक संख्याओं की जड़ें जटिल संख्याओं में मौजूद हैं)। हमें दो जटिल समाधान मिलेंगे:
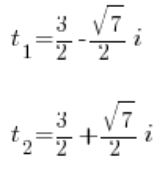
चूँकि हमने प्रतिस्थापित किया: ![]() , हमारे पास है:
, हमारे पास है:
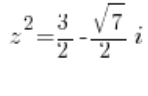
या:
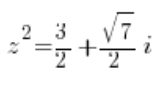
अर्थात:
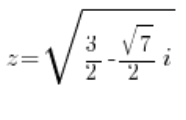
या:
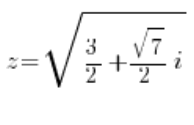
जड़ों की गणना करने के बाद (निश्चित रूप से चार जटिल जड़ें निकलेंगी), हमारे पास चार समाधान होंगे:
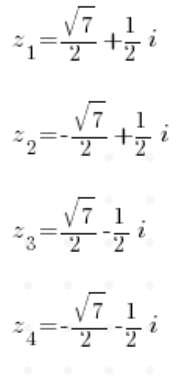
पी.एस. मैं इस और अन्य विधियों को पाठ 6 में दिखाता हूं, मेरे जटिल संख्या कोर्स में, जरूर देखें!


