Fourth Degree Polynomial Equations in Complex Numbers
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
When tackling problems using complex polynomial equations, we generally employ the same methods as we do for solving real polynomial equations in high school.
Fourth Degree Complex Equations Reducible to Second Degree
This also applies to fourth degree complex equations that can be reduced to second degree ones, meaning those where we have variables to the fourth power, to the second power, and a constant term, for example:
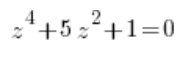
or:
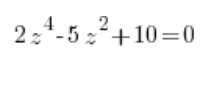
We reduce these types of complex equations to second degree complex equations by substituting 
, where 
is obviously the complex variable.
Task
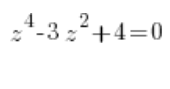
We substitute (of course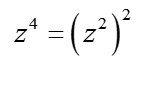 
), thus we get:
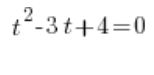
And thus we solve this equation in the usual way using the discriminant (of course, roots of negative numbers exist in complex numbers). We will obtain two complex solutions:
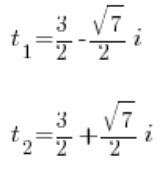
Since we substituted: , we have:
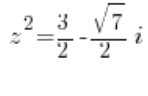
or:
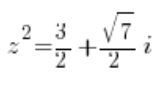
That is:
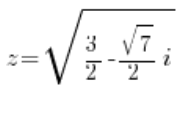
or:
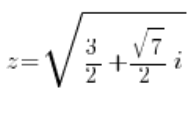
After calculating the roots (of course, there will be four complex roots), we will have four solutions:
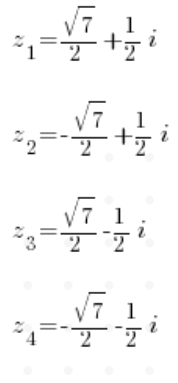
P.S. I show this and other methods in Lesson 6 of my Complex Numbers Course, check it out!
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.
