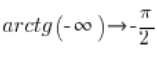चक्रवृत्तीय फलन व्याख्यान
विषय: चक्रवृत्तीय फलन
सारांश
इस व्याख्यान में, मैं चक्रवृत्तीय फलनों का परिचय दूंगा: arcsinx, arccosx, arctgx, arcctgx। ये त्रिकोणमितीय फलनों के व्युत्क्रम हैं।
व्याख्यान दो भागों में विभाजित है। पहले भाग में, मैं बस चक्रवृत्तीय फलनों के मानों की गणना कैसे जल्दी से की जाए, यह दिखाऊंगा, बिना विषय में अधिक गहराई से जाने के (इस भाग में एक वीडियो संलग्न है, जो मेरे इंटीग्रल कैलकुलस कोर्स का अंश है)।
दूसरे भाग में, मैं चक्रवृत्तीय फलनों का अधिक सटीक वर्णन करूंगा, उनके ग्राफ आदि दिखाऊंगा।
व्याख्यान को समझने के लिए आवश्यक होंगे:
- त्रिकोणमितीय फलन (उच्च विद्यालय)
भाग I
चक्रवृत्तीय फलन – “त्वरित” संस्करण
चक्रवृत्तीय फलन सरल शब्दों में त्रिकोणमितीय फलनों के व्युत्क्रम हैं। यानी arcsinx sinx का व्युत्क्रम फलन है।
इसका मतलब, अगर हम जानते हैं कि 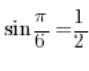 , तो इसका मतलब है कि
, तो इसका मतलब है कि ![]() ।
।
और इसी तरह:
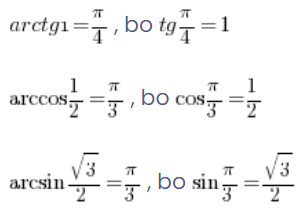
इसके अलावा हमारे पास कुछ चक्रवृत्तीय फलनों के गुणधर्म भी हैं, जो हमें नकारात्मक तर्कों के लिए भी उनके मानों की गणना करने की अनुमति देते हैं:
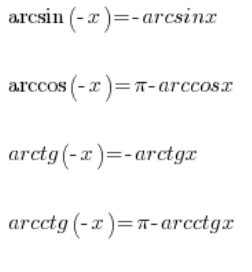
इसलिए हम इसे भी गणना कर सकते हैं:
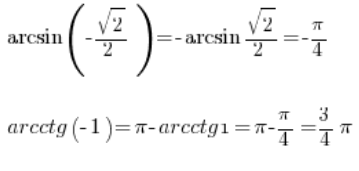
इस प्रकार, हमारे पास त्रिकोणमितीय फलनों की तालिका होने से हम आसानी से चक्रवृत्तीय फलनों के मानों का निर्धारण कर सकते हैं, बस इसे “उल्टा” पढ़कर।
मैं इसे यहाँ वीडियो में अधिक विस्तार से समझाता हूँ:
वीडियो में त्रिकोणमितीय फलनों के मौलिक मानों की तालिका – यहाँ डाउनलोड करें।
भाग II
चक्रवृत्तीय फलन – पूर्ण संस्करण
परिचय – क्यों भाग I पर्याप्त नहीं है
ऐसा लगता है कि भाग I में, हमने प्रत्येक चक्रवृत्तीय फलन को उसके संबंधित त्रिकोणमितीय फलन का व्युत्क्रम फलन के रूप में परिभाषित किया है।
आइए इसे थोड़ा औपचारिक बनाएं। हमने कहा कि उदाहरण के लिए, फलन ![]() मान
मान ![]() लेता है, जब फलन
लेता है, जब फलन ![]() इस
इस ![]() का मान
का मान ![]() होता है।
होता है।
अनुरूप:
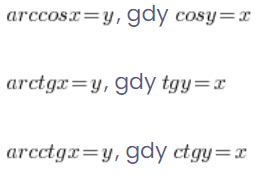
तो अगर हम ![]() की गणना करना चाहते हैं, तो हम सोचते हैं कि कौन सा कोण
की गणना करना चाहते हैं, तो हम सोचते हैं कि कौन सा कोण ![]() का कोसाइन देता है, हमें पता चलता है कि यह कोण
का कोसाइन देता है, हमें पता चलता है कि यह कोण ![]() है और हमारे पास परिणाम है:
है और हमारे पास परिणाम है: 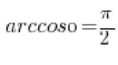 ।
।
क्या यह चक्रवृत्तीय फलनों के सभी मानों को कवर करता है?
बिल्कुल नहीं।
आइए विशिष्ट संख्याओं के साथ पूरा तर्क फिर से देखें (और शायद परंपरागत रूप से arcsinx पर स्विच करें):
यदि हम  की गणना करना चाहते हैं, तो हम सोचते हैं कि कौन सा कोण
की गणना करना चाहते हैं, तो हम सोचते हैं कि कौन सा कोण ![]() का साइन देता है, हमें पता चलता है कि यह कोण
का साइन देता है, हमें पता चलता है कि यह कोण ![]() है और हमारे पास परिणाम है:
है और हमारे पास परिणाम है:  ।
।
समस्या कहाँ है? बोल्ड वाले भाग में:
यदि हम  की गणना करना चाहते हैं, हम सोचते हैं कि कौन सा कोण का साइन
की गणना करना चाहते हैं, हम सोचते हैं कि कौन सा कोण का साइन ![]() देता है, हमें पता चलता है कि यह कोण
देता है, हमें पता चलता है कि यह कोण ![]() है और हमारे पास परिणाम है:
है और हमारे पास परिणाम है:  ।
।
दुर्भाग्य से, केवल ![]() का साइन
का साइन ![]() के बराबर नहीं है।
के बराबर नहीं है।
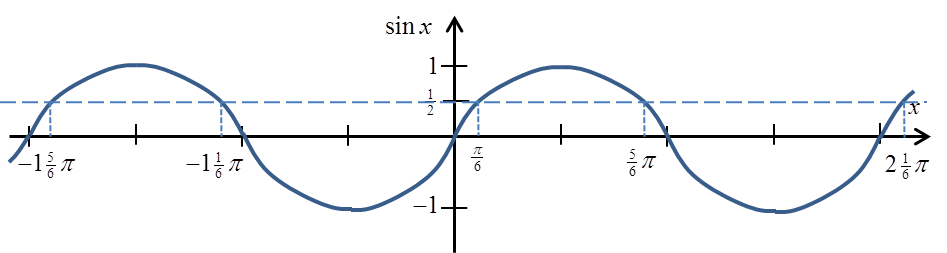
आइए sinx का ग्राफ याद करें (मैंने उस पर ![]() का मान चिह्नित किया है):
का मान चिह्नित किया है):
हम देख सकते हैं और उच्च विद्यालय से जानते हैं कि साइन का मान ![]() केवल
केवल ![]() कोण के लिए ही नहीं बल्कि इन कोणों के लिए भी लेता है:
कोण के लिए ही नहीं बल्कि इन कोणों के लिए भी लेता है: 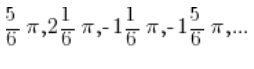
इसका मतलब 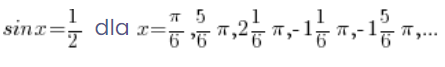
आइए अपनी arcsin गणना विधि को फिर से याद करें:
यदि हम  की गणना करना चाहते हैं, हम सोचते हैं कि कौन सा कोण का साइन
की गणना करना चाहते हैं, हम सोचते हैं कि कौन सा कोण का साइन ![]() देता है, हमें पता चलता है कि यह कोण
देता है, हमें पता चलता है कि यह कोण ![]() है और हमारे पास परिणाम है:
है और हमारे पास परिणाम है:  ।
।
लेकिन अब हम जानते हैं कि सिर्फ sin![]()
![]() ही नहीं देता, इसलिए ऐसा लगता है:
ही नहीं देता, इसलिए ऐसा लगता है:
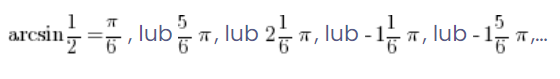
इसका मतलब है कि arcsinx बिल्कुल भी फ़ंक्शन नहीं है, क्योंकि एक आर्ग्यूमेंट के लिए कई मान हैं!
किसी चीज़ का arcsin कितना है, इस सवाल का स्पष्ट उत्तर देना तब पूरी तरह से असंभव होगा।
यह भी कल्पना करना आसान है कि इसी तरह की समस्या किसी भी त्रिकोणमितीय फ़ंक्शन के साथ होती है।
ज्यादा पेशेवर तरीके से कहें तो: ये फ़ंक्शन एक-एक मान वाले नहीं हैं, इसलिए उनके विपरीत फ़ंक्शन मौजूद नहीं हैं। प्रत्येक त्रिकोणमितीय फ़ंक्शन में, प्रत्येक मान अनंत संख्या में आर्ग्यूमेंट्स के लिए प्राप्त होता है (वे आवर्ती होते हैं, है ना?), इसलिए उनके विपरीत फ़ंक्शन को निर्धारित करने की कोशिश करते समय, हमें प्रत्येक आर्ग्यूमेंट के लिए अनंत मान प्राप्त होंगे। और ऐसा फ़ंक्शन में नहीं हो सकता।
क्या करें?
यह काफी सरल है, यह कहने के लिए कि यह प्राचीन है। प्रत्येक त्रिकोणमितीय फ़ंक्शन को काटा जा सकता है ताकि परिणाम एक-एक मान वाला फ़ंक्शन हो।
तो चलिए सही तरीके से सभी 4 चक्रवृत्तीय फ़ंक्शंस को परिभाषित करते हैं:
arcsinx
sinx फ़ंक्शन के ग्राफ़ को याद करें:
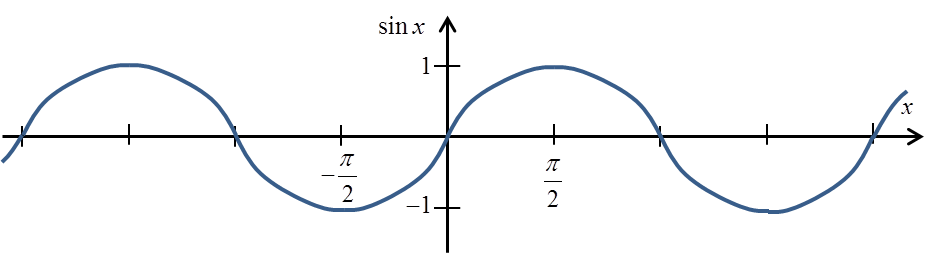
अगर हम मान लें कि हम इसे ![]() अंतराल में काटते हैं, तो हमें ऐसा ग्राफ़ मिलेगा:
अंतराल में काटते हैं, तो हमें ऐसा ग्राफ़ मिलेगा:
![Wykres sinx w przedziale [0,pi] Obraz3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
दुर्भाग्य से, यह वह नहीं है जो हम चाहते हैं, क्योंकि यह अभी भी एक-एक मान वाले फ़ंक्शन का ग्राफ़ नहीं है, और ![]() का मुद्दा अभी भी मौजूद है:
का मुद्दा अभी भी मौजूद है:
![Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2 Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
इसलिए हम सहमत हैं कि sinx फ़ंक्शन को अलग तरीके से काटें, आर्ग्यूमेंट्स के लिए 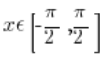 :
:
![Wykres funkcji sinx dla x należących do [-pi/2,pi/2] Wykres funkcji sinx dla x należących do [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
अब यह एक-एक मान वाला फ़ंक्शन है और इसमें एक विपरीत फ़ंक्शन arcsinx है।
arcsinx फ़ंक्शन का ग्राफ़ कुछ इस प्रकार होगा:

इसका डोमेन अंतराल ![]() नहीं है।
नहीं है।
इसलिए, arcsinx फ़ंक्शन की सटीक परिभाषा है:
![]() ।
।
arccosx
cosx फ़ंक्शन भी एक-एक मान वाला फ़ंक्शन नहीं है:
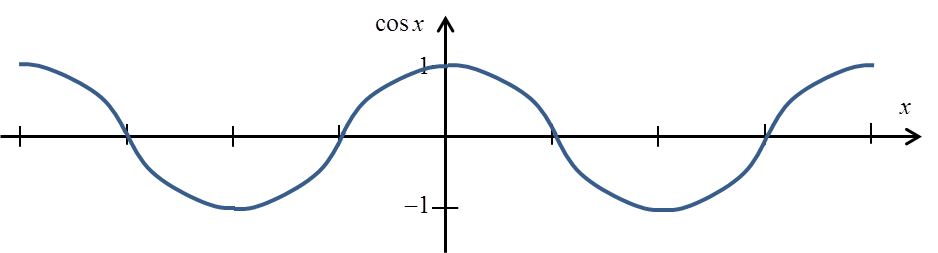
एक-एक मान वाला फ़ंक्शन प्राप्त करने के लिए हमें इसे ![]() अंतराल तक काटना होगा:
अंतराल तक काटना होगा:
![Wykres funkcji cosx obciętej do przedziału [0,pi] Wykres funkcji cosx obciętej do przedziału [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
इस प्रकार परिभाषित फ़ंक्शन पहले से ही एक-एक मान वाला है और इसमें एक विपरीत फ़ंक्शन arccosx है।
इसका ग्राफ़ लगभग इस प्रकार होगा:
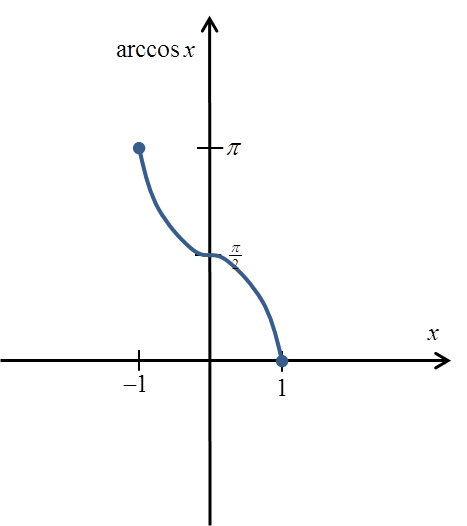
और इसकी सटीक परिभाषा है:
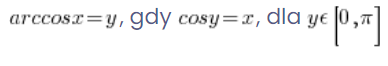 ।
।
arctgx
tgx फ़ंक्शन का ग्राफ़ इस प्रकार है:

यह भी एक-एक मान वाला फ़ंक्शन नहीं है! हम इसे इस प्रकार काट सकते हैं:
![Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2] Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
इस प्रकार हमें एक-एक मान वाला फ़ंक्शन प्राप्त होता है।
arctgx फ़ंक्शन का ग्राफ़ इस प्रकार है:

और इसकी सटीक परिभाषा इस प्रकार है:
![]() , y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right) के लिए।
, y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right) के लिए।
हम यह भी देख सकते हैं कि ग्राफ़ से कुछ दिलचस्प गुण निकलते हैं, उदाहरण के लिए:
- arctgx फ़ंक्शन का डोमेन पूरे वास्तविक संख्याओं का समूह है (हम किसी भी संख्या का arctg निकाल सकते हैं)


arcctgx
ctgx फ़ंक्शन के ग्राफ़ से:

हम एक-एक मान वाला टुकड़ा काटते हैं:
arcctgx फ़ंक्शन का ग्राफ़ इस प्रकार है:
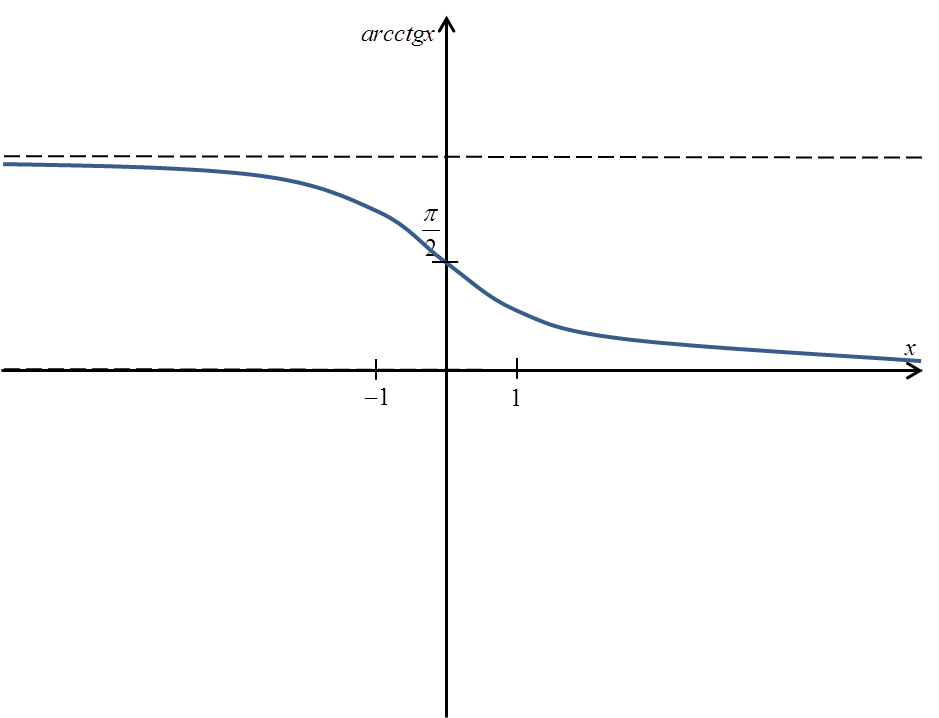
arcctgx की सटीक परिभाषा इस प्रकार होगी:
![]() ।
।
हम देख सकते हैं कि:
- arcctgx फ़ंक्शन का डोमेन पूरे वास्तविक संख्याओं का समूह है (हम किसी भी संख्या का arcctg निकाल सकते हैं)


नोट
कई कैलकुलेटरों और सामान्य रूप से गणितीय अभिव्यक्तियों (विशेष रूप से पश्चिमी) में, त्रिकोणमितीय फ़ंक्शंस के विपरीत फ़ंक्शन को “arcus” के रूप में नहीं दर्शाया जाता है, बल्कि घातांक -1 से। उदाहरण के लिए, arcsinx को ![]() के रूप में लिखा जाता है। यदि आप जानते हैं कि यह किस बारे में है, तो कोई समस्या नहीं है। हालाँकि, आप एक बड़ी गलती कर सकते हैं और sinx के विपरीत फ़ंक्शन को
के रूप में लिखा जाता है। यदि आप जानते हैं कि यह किस बारे में है, तो कोई समस्या नहीं है। हालाँकि, आप एक बड़ी गलती कर सकते हैं और sinx के विपरीत फ़ंक्शन को ![]() फ़ंक्शन के साथ भ्रमित कर सकते हैं – जो arcsinx से पूरी तरह से अलग फ़ंक्शन है।
फ़ंक्शन के साथ भ्रमित कर सकते हैं – जो arcsinx से पूरी तरह से अलग फ़ंक्शन है।