ऊपर दिए गए समीकरणों के सिस्टम में पैरामीटर ‘a’ की गणना करें, यह जानते हुए कि यह असंगत है।
मुख्य मैट्रिक्स की रैंक की गणना स्कीमेटिक तरीके से शुरू करने के बजाय, हम विस्तारित मैट्रिक्स की रैंक निर्धारित करते हैं:
…यह दो के बराबर है, क्योंकि इस मैट्रिक्स में आप दूसरे क्रम का गैर-शून्य डिटर्मिनेंट निकाल सकते हैं (और आप बड़ा नहीं प्राप्त कर सकते हैं):
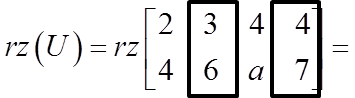
इसलिए विस्तारित मैट्रिक्स की रैंक 2 है।
क्रोनेकर-कापेली प्रमेय का उपयोग
तो मुख्य मैट्रिक्स की रैंक क्या होनी चाहिए?
हम जानते हैं कि सिस्टम असंगत है, और क्रोनेकर-कापेली प्रमेय से हम जानते हैं कि यह असंगत होगा जब मुख्य मैट्रिक्स की रैंक विस्तारित मैट्रिक्स की रैंक से अलग होगी। हम यह भी जानते हैं कि मुख्य मैट्रिक्स की रैंक हमेशा विस्तारित मैट्रिक्स की रैंक से कम या बराबर होती है (मुख्य मैट्रिक्स विस्तारित मैट्रिक्स में समाहित होती है)। इसलिए मुख्य मैट्रिक्स की रैंक 1 या 0 होनी चाहिए (विस्तारित मैट्रिक्स की रैंक से भिन्न होने के लिए)।
मुख्य मैट्रिक्स की रैंक होगी:
हम देखते हैं कि यह निश्चित रूप से 0 नहीं होगी (केवल शून्य मैट्रिक्स की रैंक 0 होती है) – इसलिए इसे 1 होना चाहिए। जब पहली और दूसरी पंक्ति समानुपाती होती हैं तो रैंक एक होगी (तब हम उनमें से एक को हटा देंगे)। हम देखते हैं कि पहली पंक्ति को दो से गुणा करने पर दूसरी पंक्ति मिलती है, यदि केवल a 8 के बराबर हो।
तो तेजी से और बिना बड़े गणनाओं के हम उत्तर पर पहुँचते हैं:
