Currently Empty: zł0.00
Krystian Karczyński- 28 जून 2024
- Comment 0
शीर्षक में पूछे गए प्रश्न का उत्तर देने के लिए, हमें तिरछी आसमोट की परिभाषा तक जाने की जरूरत नहीं है, हमें केवल यह जानना है कि एक फ़ंक्शन क्या है।
जैसा कि अक्सर गणित में होता है – हम अस्थायी रूप से मान लेंगे कि फ़ंक्शन के ग्राफ में 
पर दो अलग-अलग तिरछी आसमोट हैं और दिखाएंगे कि इस धारणा को मानने से निश्चित रूप से विरोधाभास उत्पन्न होगा, इसलिए इस धारणा को स्वीकार नहीं किया जा सकता।
ग्राफ
ग्राफ में ये तिरछी आसमोट इस प्रकार दिख सकती हैं:
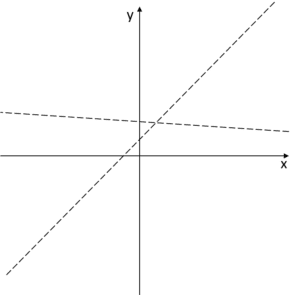और पर फ़ंक्शन का ग्राफ इन तिरछी आसमोट के करीब होना चाहिए, इसलिए यह इस प्रकार दिखेगा:
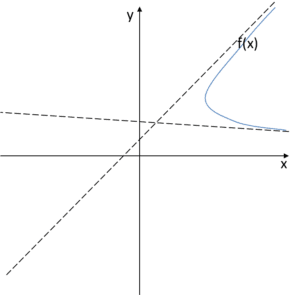और? क्या ऐसा हो सकता है? क्या फ़ंक्शन का ग्राफ ऐसा दिख सकता है? या हमारे पास यहां कोई समस्या है?
समस्या
बेशक, हमारे पास एक समस्या है। ऊपर जो दिखाया गया है वह फ़ंक्शन का ग्राफ नहीं हो सकता। चलिए परिभाषा की ओर लौटते हैं, फ़ंक्शन परिभाषा के अनुसार एक निरूपण है जो प्रत्येक x तर्क के लिए सिर्फ एक y मान निर्दिष्ट करता है। हमारे ग्राफ से क्या निष्कर्ष निकलता है?
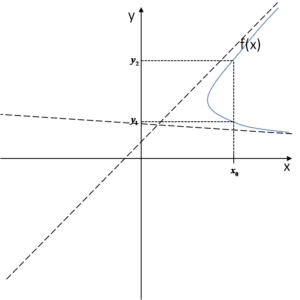हम देख सकते हैं कि उदाहरण के लिए तर्क 
के लिए दो मान निर्दिष्ट हैं – 
और 
। और यह फ़ंक्शन ग्राफ में नहीं हो सकता, क्योंकि प्रत्येक x तर्क के लिए सिर्फ एक y मान होना चाहिए।
इसलिए पर फ़ंक्शन के पास दो अलग-अलग तिरछी आसमोट नहीं हो सकती। 
के लिए भी पूरा तर्क इसी प्रकार से दोहराया जा सकता है 🙂
