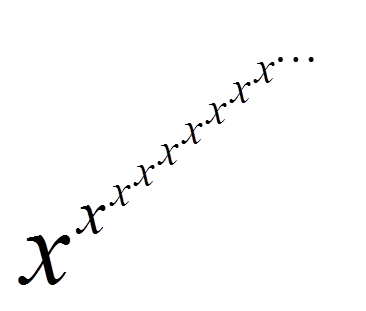
x do x do x … Co Robić? (Przykład z Morałami)

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

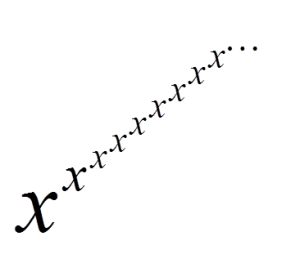Jako ciekawostkę policzę granicę funkcji:

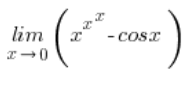
Ciekawsze od samych obliczeń będą dwa morały, które można z nich wyciągnąć. Ale morały na koniec (czy ktoś widział historyjkę z morałem na początku)? Teraz liczę:

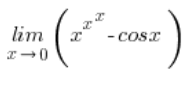
Na początku patrzę, co do czego zmierza i mam:

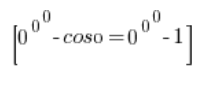
Czyli nie mam pojęcia co do czego zmierza, bo nie wiem nawet, do czego zmierza (jest to symbol nieoznaczony), a co dopiero takie dziwadło jak: .

Wygląda jednak na to, że z cosinusem nie ma problemów, liczę więc na boku, do czego zmierza samo:

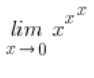
Będę stosował dojście do d’Hospitala (pokazałem dokładnie o co chodzi w moim Kursie ), czyli skorzystam ze wzoru ():

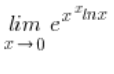
Ale nadal nie jest fajnie, bo mam dalej w wykładniku symbol nieoznaczony , przekształcam więc to drugi raz:

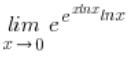
Teraz mogę już spokojnie brać się do roboty. Liczę na boku:

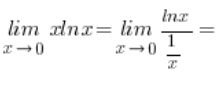
, mam więc symbol nieoznaczony de l’Hospitalem więc to:

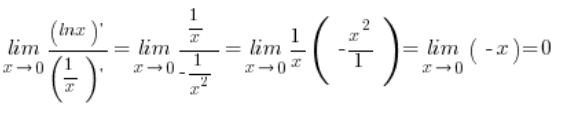
Czyli mam policzone na boku, że: .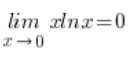

Wracając więc do granicy:

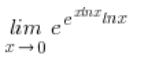
Wiem już, że mam tu sytuację:

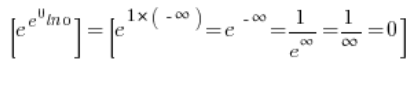
Czyli okazało się, że:

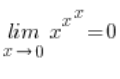
Zatem cała moja granica:

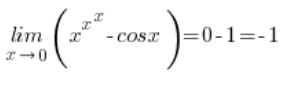
A cosinus był tylko na postrach.

Morały z tej historii

Są dwa.

1. W trudniejszych granicach zawsze można i czasem trzeba brać jej kawałek i obliczać, do czego zmierza “na boku”.
2. Czasami niektóre fragmenty w formule granicy mogą być dodane tak jak ten cosinus. Okazało się, że nic z nim nie muszę kombinować, tylko podstawić zero na końcu.