Twierdzenie o trzech funkcjach - przykład (VIDEO) | Blog eTrapez

Krystian Karczyński

Znane dobrze twierdzenie o trzech ciągach ma swój odpowiednik dla funkcji. W filmiku poniżej rozwiązuję granicę:

\underset{x\to \infty }{\mathop{\lim }}\,\frac{x-\sin 3x}{2x+\sin 4x}

…korzystając właśnie z twierdzenia o trzech funkcjach.

Pokazuję też na nim ważną zasadę dotyczącą szukania ograniczeń ułamków, którą stosuje się również w innych działach matematyki (np. w kryterium porównawczym szeregów).

Filmik jest odpowiedzią na pytanie w komentarzach do innego postu na blogu.

Jeśli masz jakieś pytania lub wątpliwości – wal śmiało w komentarzach pod postem 🙂

konometria jest dosyć młodą dziedziną wypływającą z ekonomii i matematyki. W praktyce, dzięki modelom ekonometrycznym, możesz „zmierzyć gospodarkę”.Polega to konkretnie na zmierzeniu, jak zachowuje się jedna zmienna w zależności od innych. I na podstawie analizy tego, co było, możesz określać, co będzie się działo w przyszłości.

Wykorzystasz do tego przeróżne obliczenia, testy, schematy. Jedne będą bardzo proste, inne trudniejsze. Jednak najczęściej będzie się liczyło nie to, jak dojdziesz do wyniku, ale jak go zinterpretujesz, odczytasz i jakie wnioski wyciągniesz.

Poniższe Wykłady dotykają najważniejszych pojęć teoretycznych. Jestem przekonana, że pomogę Ci odkrywaniu tego, czym jest ekonometria. I przy okazji uda Ci się zaliczyć ten przedmiot na studiach.

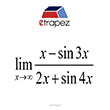
4 Komentarzy

Ola
12 grudnia 2013 at 00:00

Witam, świetnie Pan tłumaczy, przykłady są bardzo pomocne, kursy przemyślane i przystęp\ne. Dzięki nim jakoś łatwiej i przyjemniej 😉 podchodzi się do nauki analizy i algebry,

PS Z e-trapezem bez problemu zaliczyłam I kolokwium z analizy, moi znajomi również. Gratuluję doskonałego pomysłu i jego realizacji, oby tak dalej:)

Odpowiedz
1. Krystian Karczyński
  12 grudnia 2013 at 10:16
  
  Dzięki, gratuluję!
Zbigniew Płonka
9 lutego 2013 at 09:08

Polecam użyć zabawnej historii o 2 policjantach co prowadzą napranego gościa 🙂 … jeżeli dwoch niebieskich idzie w prawo to naprany nie ma wyjścia i również ..

ZP

Odpowiedz
1. Krystian Karczyński
  12 lutego 2013 at 22:38
  
  W Kursie użyłem, ta historyjka jest nawet w Wikipedi:
  http://pl.m.wikipedia.org/wiki/Twierdzenie_o_trzech_ci%C4%85gach

Dodaj komentarz Anuluj pisanie odpowiedzi

Nasze "Wykłady"

Wirtualny Krystian AI

Wirtualny nauczyciel AI działający w przeglądarce internetowej.