Wykazywanie, że sinx nie osiąga granicy przy x dążącym do nieskończoności
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka koło Szczecina. Lubi spacery po lesie, plażowanie i piłkę nożną.
Mamy granicę funkcji:
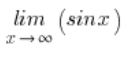
Intuicyjnie czujemy, że powyższa granica nie istnieje. x-sy są coraz większe i większe, a wartości sinusa “majtają się” cały czas pomiędzy -1 a 1.
Formalny dowód
Jak jednak formalnie to wykazać i udowodnić?
Z definicji granicy funkcji przy x dążącym do nieskończoności wiemy, że granica istnieje, jeśli dla każdego ciągu argumentów funkcji rozbiegającego w 
odpowiadający im ciąg wartości funkcji zbiega do tej samej liczby (wtedy ta liczba właśnie jest tą granicą).
Żeby pokazać więc, że taka granica nie istnieje wystarczy wziąść dwa byle jakie ciągi argumentów rozbiegające w i pokazać, że odpowiadające im ciągi wartości zbiegają do dwóch różnych liczb.
Wiemy, że funkcja sinus jest okresowa, mogą to być więc na przykład ciągi:
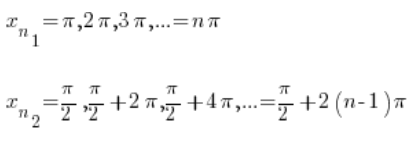
Oczywiście oba ciągi rozbiegają w nieskończoność przy 
Teraz spójrzmy na odpowiadające tym ciągom ciągi wartości funkcji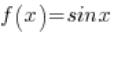 
:
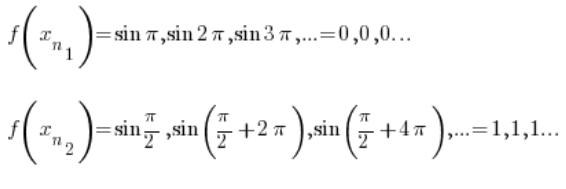
Oczywiście pierwszy ten ciąg zbiega do 0, a drugi ciąg zbiega do 1.
To wystarczy, żeby udowodnić, że granica funkcji:
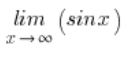
nie istnieje.
Jedna z wielu opinii o naszych Kursach...
Śmieszne pieniądze za porządny kurs, a wielu wykładowców tłumaczy bez pasji i nawet na konsultacjach im się nie chce dodatkowo tłumaczyć, a tutaj mogę kilka razy tego samego słuchać jak potrzebuje.Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Jedno trzeba przyznać, jakby takich ćwiczeniowców i wykładowców jak p. Karczyńskiego miała każda uczelnia, to Polska byłaby u szczytu rozwoju cywilizacji. Niestety realia takie że jedyne co podszkoliłem do tej pory na matmie to kaligrafie.. Polecam gorąco i dziękuję że poświęcił Pan czas dla takich jak my !! : D
czy ktos pomoze zbadac zbieznosc calki okreslonej na przedziale od zera do nieskonczonosci i funkcji podcalkowej xsinxdx
Jak należało by to zrobić dla sinx^3?
Napisałam pi/2 dlatego, że stwierdziłam że nie moge zastosować wzoru na limn->- sinx/x =1
dlatego że w tym wzorrze lim dąży do 0 a w rozwiązywanym preze mnie przykładzie lim n dąży do nieskończoności.
Wobec tego zrobiłam małą szaloną twórczość 😀 i sinx/sinx razy sin , potem poskracałam wyszło mi sin 1 a z tabelki finkcji trygonometrycznych napisałam że sin1 =pi/2
Miałam ten przykład dzisiaj na kolosie i mam szczere wątpliwości czy nie napisałam głupot :/
Proszę mi pomóc – jaka miało być prawidłowe rozwiazanie?
Witam, prawidłowe rozwiązanie to 0🙂
Oczywiście, nie można zastosować wzoru \underset{x\to 0}{\mathop{\lim }}\,\frac{\sin x}{x}=1, bo x nie dąży do zera.
To trzeba ruszyć twierdzeniem o trzech funkcjach, które omawiam w tym poście . To jest taki jakby odpowiednik twierdzenia o trzech ciągach.
sinx jest zawsze mniejsze lub równe od 1 i większe lub równe od -1, zatem na pewno:
\frac{-1}{x}\le \frac{\sin x}{x}\le \frac{1}{x}
Teraz liczę granice z funkcji ograniczających z dołu i z góry i pokazuję, że są równe sobie:
\underset{x\to \infty }{\mathop{\lim }}\,\frac{1}{x}=0
\underset{x\to \infty }{\mathop{\lim }}\,\frac{-1}{x}=0
Zatem, na mocy twierdzenia o trzech funkcjach, wynika stąd, że: \underset{x\to \infty }{\mathop{\lim }}\,\frac{\sin x}{x}=0
No zajebiście wytłumaczone tutaj, tak samo zrobiłem te zadanie ;P
A w takim razie mam pytanie. Jeśli mam
lim n-> nieskończoności z sinx/x to jaki będzie wynik tej granicy? Mnie wysżło pi/2 ale mam wątpliwości czy to tak ma być ….
Nie ‘wziąść’ tylko ‘wziąć’, jako humanista czuje się zobowiązany zwrócić Panu uwagę.
Dziękuję. Humanistyczny głos jest bardzo potrzebny na tym blogu 🙂