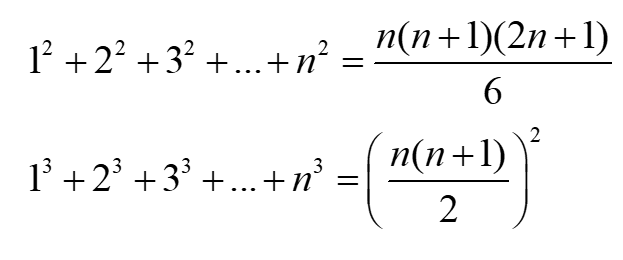
Granice ciągu z sumą kwadratów lub sumą sześcianów

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

W granicach ciągów bywa czasami tak:

a czasami nawet tak:

${lim}under{n{right}infty}{1+2^3+3^3+...+n^3}/n^4$

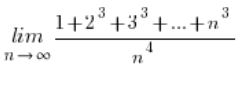
Co wtedy?

Odpowiedź jest prosta:

wzory na sumę kwadratów i na sumę sześcianów kolejnych liczb naturalnych.

Szły one tak:

$1^2+2^2+3^2+...+n^2={n(n+1)(2n+1)}/6$

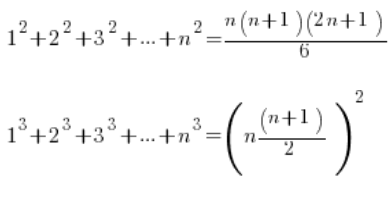
Wzory – jak to wzory – do wyuczenia na pamięć. O ile miałeś podobne przykłady i ich rzeczywiście potrzebujesz.

Znając wzorki policzenie naszych granic staje się banalne:

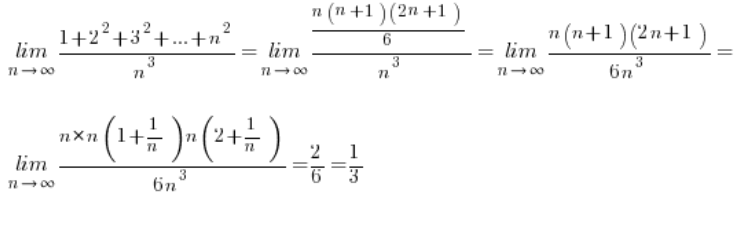
${lim}under{n{right}infty}{1+2^2+3^2+...+n^2}/n^3={lim}under{n{right}infty}{{n(n+1)(2n+1)}/6}/n^3={lim}under{n{right}infty}{n(n+1)(2n+1)}/{6n^3}=$

$={lim}under{n{right}infty}{n*n(1+1/n)n(2+1/n)}/{6n^3}=2/6=1/3$

Kolejna granica:

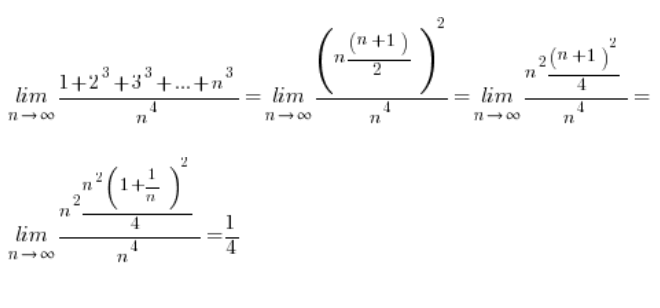
${lim}under{n{right}infty}{1+2^3+3^3+...+n^3}/n^4={lim}under{n{right}infty}(n(n+1)/2)^2/n^4={lim}under{n{right}infty}{{n^2}(n+1)^2/4}/n^4=$

${lim}under{n{right}infty}{{n^2}{{n^2}(1+1/n)^2}/4}/n^4=1/4$

Dowody indukcyjne dla wzorów

Prawdziwości wzorów można dosyć łatwo dowieść indukcyjne (przynajmniej jeszcze parenaście lat temu był to zupełny standard w szkole średniej). Zrobię to dla wzoru:

1. $1^2+2^2+3^2+...+n^2={n(n+1)(2n+1)}/6$

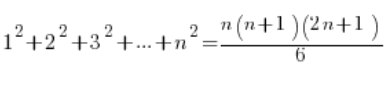
1 Krok indukcyjny

Sprawdzamy prawdziwość wzoru dla n=1:

$1^2={1(1+1)(2*1+1)}/6$

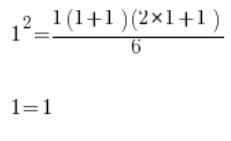
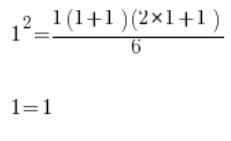
Zgadza się

2 Krok indukcyjny

Przyjmujemy założenie, że dla pewnego naturalnego n:

$1^2+2^2+3^2+...+n^2={n(n+1)(2n+1)}/6$

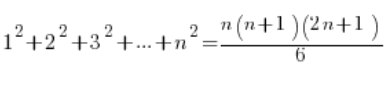
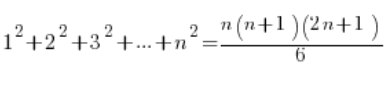
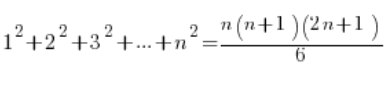
3 Krok indukcyjny

Wykazujemy tezę (korzystając z przyjętego założenia), że dla n+1 wzór także zachodzi, tzn:

$1^2+2^2+3^2+...+n^2+(n+1)^2={(n+1)(n+1+1)(2(n+1)+1)}/6$

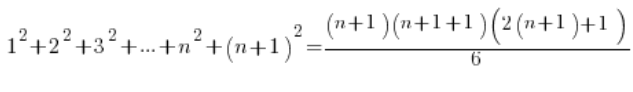
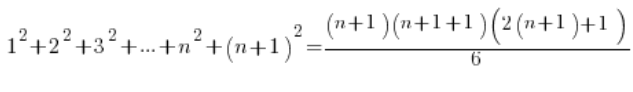
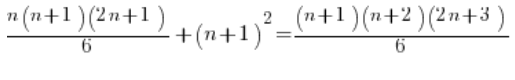
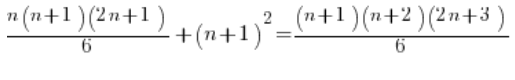
Po lewej stronie zamiast wstawiam formułę z założenia, po prawej po prostu porządkuję:

${n(n+1)(2n+1)}/6+(n+1)^2={(n+1)(n+2)(2n+3)}/6$

I dalej zamiast smarować na siłę działam trochę subtelniej:

${n(n+1)(2n+1)}/6+(n+1)^2={(n+1)(n+2)(2n+3)}/6$ /

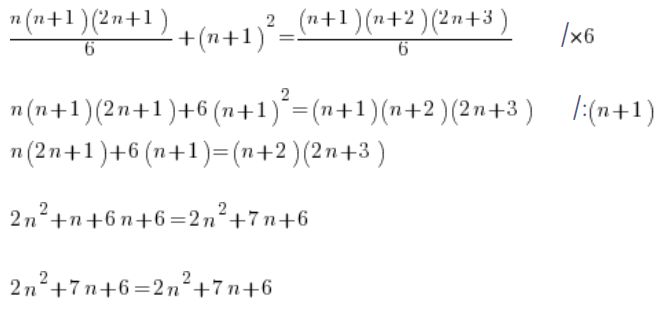
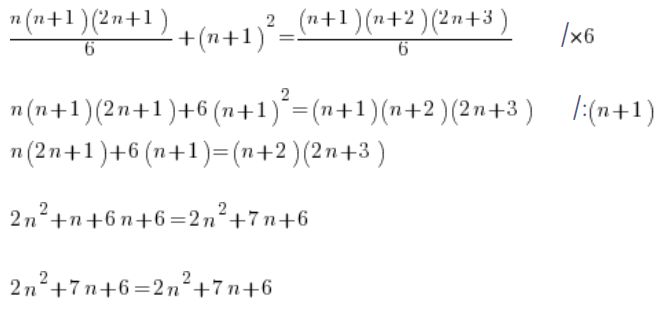
Czyli teza wykazana. Wzór wykazany indukcyjnie.

Was zapraszam do indukcyjnego wykazania drugiego wzoru, na sumę sześcianów:

Jedna z wielu opinii o naszych Kursach...

Zakupiłem cały pakiet kursów mimo, że już dobijam do wieku emerytalnego i jestem po studiach technicznych. Nie znaczy to jednak , że zainteresowanie matematyką osłabło. Wręcz przeciwnie! Jestem w trakcie ich „konsumowania”. Mogę stwierdzić jedno – to co robicie jest fantastyczne. Pomoc dla wszystkich, czy to uczniów szkół ponadpodstawowych czy też dla studentów. To nie są pieniądze wyrzucone w błoto!

Aleksander M.

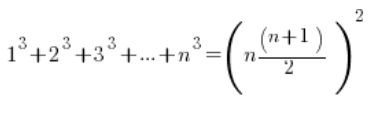
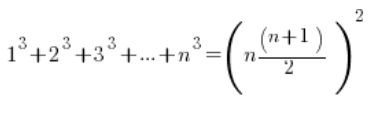
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?

Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.

Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.

Dodaj komentarz Anuluj pisanie odpowiedzi

Wprowadzenie do granic ciągów. Wyciąganie przed nawias najwyższej potęgi. Pełna DARMOWA Lekcja Kursu Granice [VIDEO]

13 stycznia 2022 / Krystian Karczyński

Czytaj więcej

Elementy kombinatoryki: reguła mnożenia, permutacje, wariacje, kombinacje. Pełna darmowa Lekcja Kursu Prawdopodobieństwo. [VIDEO]

03 stycznia 2022 / Krystian Karczyński

Czytaj więcej

Wprowadzenie do macierzy: dodawanie, odejmowanie, mnożenie macierzy. Kurs Macierze – pełna Lekcja 1. [VIDEO]

03 stycznia 2022 / Krystian Karczyński

Czytaj więcej

Najpopularniejsze Kursy w sierpniu

Zobacz demo