Dowodu nie wymyśliłem sam, tylko wziąłem z książki G.M.Fichtenholz’a “Rachunek różniczkowy i całkowy” (z małą przeróbką na samym końcu) – oczywiście rozszerzając o wszystkie przejścia, dla lepszego zrozumienia, co się bierze z czego. Do wykazania powyższej granicy wykorzystam definicję Cauchy’ego granicy funkcji.
Wykazanie pewnej pożytecznej dla dowodu nierówności
Lemat
Dla :
.
Dowód
Czyli wykażemy jakby nierówność:
, która zachodzi dla
Tą nierówność warto zapamiętać, przydaje się nie tylko do tego dowodu, ale do różnych innych rzeczy w analizie matematycznej (na przykład do szacowania szeregów liczbowych w kryterium porównawczym). Poza tym w ogóle jest ciekawa sama w sobie, prawda? 🙂
No to do dzieła, dowiedźmy tej nierówności.
Na początku narysujmy coś takiego:
Mamy okrąg o środku w punkcie O, promieniu R, cięciwie AB, kącie AOB równym i stycznej BC do okręgu w punkcie B.
Zwróćmy uwagę na trzy rzeczy:
Pole trójkąta OAB
Pole wycinka koła o kącie AOB (nie myl z trójkątem z punktu 1!)
Pole trójkąta COB
Oczywistym jest, że zawsze:
Pole trójkąta OAB < Pole wycinka AOB < Pole trójkąta COB
Teraz po kolei wyznaczmy te pola:
1. Pole trójkąta OAB
Ze szkoły średniej pamiętamy alternatywny wobec oklepanego “” wzór:
Pole trójkąta = bok razy bok razy sinus kąta pomiędzy nimi.
W naszym konkretnym trójkącie oba boki mają długość R (promień koła), zatem pole trójkąta równe jest:
2. Pole wycinka OAB
Pole wycinka można wyznaczyć na przykład z proporcji (albo gotowym wzorkiem – jak się zna). Polu całego okręgu odpowiada kąt (w radianach), a polu wycinka (które mamy właśnie policzyć), kąt radianów. Proporcje wyglądać będą tak:
Mnożąc na krzyż, tak jak to się w proporcjach działało (szukamy P(AOB)) otrzymamy nasze pole wycinka:
3. Pole trójkąta COB
Ten trójkąt jest trójkątem prostokątnym (bo prosta CB jest styczną). Zatem można przyjąć, że odcinek OB (równy R) to jego podstawa, a odcinek CB – wysokość i skorzystać ze standardowego .
Zamieszajmy jednak do tego wzoru kąt , zamiast odcinka . Wiemy, że w tym trójkącie:
Mnożąc obie strony równości przez R otrzymamy:
…które możemy podstawić do wzoru na pole trójkąta COB, otrzymując:
Mamy wyznaczone wszystkie 3 pola.
Wróćmy więc do nierówności:
Pole trójkąta OAB < Pole wycinka AOB < Pole trójkąta COB
Podstawiając wyliczone pola otrzymamy:
Dzielimy obustronnie przez (możemy, bo promień okręgu jest większy od zera) i otrzymujemy:
A jest to dokładnie nierówność, którą mieliśmy udowodnić! I udowodniliśmy sposób 🙂
Wnioski z udowodnionej nierówności
Wyjdźmy zatem z udowodnionej już nierówności i przekształćmy ją trochę:
Najpierw rozbijemy ja na dwie:
1.
Dzielimy ją obustronnie przez x (możemy, bo x z założenia jest – czyli różne od zera i dodatnie, nie zmieni się więc znak nierówności):
2.
Jak wiemy :
Po przemnożeniu przez cosx (możemy, ze względu na założenie dotyczące x-sów):
I podzieleniu przez x (możemy ze względu na założenie odnośnie x):
Mamy więc przekształcone dwie nierówności:
Które możemy połączyć i zapisać:
Odejmując stronami 1 otrzymamy (jeśli chcesz, możesz to rozpisać z rozbiciem na dwie nierówności):
Mnożymy stronami przez -1 (zmieni to znaki nierówności):
Zapisujemy zgrabniej:
Zajmijmy się :
Na początku powtórzyć musimy sobie niestety pewien wzór trygonometryczny, mianowicie wzór na cosinus podwojonego kąta:
A więc (z tego wzoru):
Czyli:
Rozbijając jedynkę z jedynki trygonometrycznej i wchodząc z minusem w nawias otrzymam:
Czyli:
Wracając więc do naszej nierówności:
Możemy ją zapisać jako:
Zajmijmy się teraz .
Jest prawdą, że:
bo dla x z założenia z przedziału wartości sinusa są ułamkami z przedziału (0,1), a takie ułamki podniesione do kwadratu są mniejsze niż przed podniesieniem (na przykład ).
Jest także prawdą, że:
bo po podzieleniu nierówności przez 2 otrzymamy:
a to, że sinus z czegoś jest mniejszy od tego czegoś wykazaliśmy w lemacie () na początku.
Zatem wracając do naszej głównej nierówności:
Skracając:
Z powyższej nierówności wynika poniższa:
– wartość bezwzględna to odległość od zera, zatem nie zmieni się ona przy zmianie znaku x na ujemny, dopóki oczywiście x pozostaje pomiędzy 0 a .
Ze względu na to, że w wartościach bezwzględnych :
Powtórzmy, wykazaliśmy, że zachodzi nierówność (dla ).
Definicja granicy funkcji Cauchy’ego
Przypomnijmy: jeśli chcemy wykazać z definicji granicy funkcji Cauchy’ego, że musimy pokazać, że zawsze znajdziemy takie , że dla dowolnego zachodzić będzie:
Czyli:
Sprawa jest więc prosta: jeżeli obierzemy sobie byle jaki – zawsze możemy dobrać do niego takie jako liczbę większą od zera, mniejszą od epsilona i należącą do przedziału .
Z nierówności nasze x-sy będą mniejsze od delty, a skoro pokazaliśmy wcześniej, że to prawdą jest, że:
Czyli wykazaliśmy, dla takiej :
Pokazaliśmy więc z definicji Cauchy’ego, że:
Pisząc tego posta korzystałem z…
1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.
Czy mając udowodnioną nierównośćmożna skorzystać z twierdzenia o granicy trzech funkcji?więcCzy zastosowałem to twierdzenie poprawnie? Z góry dziękuję za odpowiedź 🙂
Według mnie, tak. Spełnione są założenia twierdzenia ale tylko dla x > 0, więc podobne rozumowanie trzeba by było przeprowadzić również dla x < 0.Pozdrawiam,Adam
Co do poprzedniego pytania to sobie poradziłam . Mam mały problem z granicą funkcji x dąży do minus nieskończoności (1+1/x)^x wydaje mi się że rozwiązaniem będzie liczba e ale nie wiem jak to zapisać
Korzystamy z plików cookies w celu dostosowania jej treści, jeśli będziesz na nią wracał; stosowania narzędzi analitycznych (Google Analytics, Crazyegg); marketingowych (Google Ads, Facebook Ads); widgetów matematycznych (Wolfram|Alpha) oraz embedowania treści ze stron zewnętrznych (YouTube, Vimeo). Cookies funkcjonują przez okres do 24 miesięcy, chyba że wcześniej je wyczyścisz. Dostęp do cookies mają podmioty trzecie wskazane w nawiasach. Poprzez kliknięcie “Zaakceptuj wszystkie”, wyrażasz zgodę na użycie WSZYSTKICH ciasteczek. Możesz też dostosować swoje zgody modyfikując Ustawienia. Czytaj więcej
Używamy ciasteczek, aby ulepszyć funkcjonowanie strony eTrapez. Podzieliliśmy te ciasteczka na kategorie. Niektóre z nich uznaliśmy za "niezbędne". Przechowujemy je w Twojej przeglądarce, ponieważ zapewniają podstawowe funkcjonalności strony. Inne ciasteczka uznaliśmy za mniej ważne i przechowujemy je w Twojej przeglądarce tylko za Twoją zgodą. Masz możliwość zablokowania tych ciasteczek.
Ponadto, oprócz naszych własnych, wewnętrznych ciasteczek, używamy także ciasteczek zewnętrznych firm, takich jak Facebook, Google, Vimeo.
Niezbędne ciasteczka są potrzebne do podstawowego działania strony. Zapewniają najbardziej kluczowe funkcjonalności, zabezpieczenia i zgodność z wymogami prawnymi.
Wszystkie inne ciasteczka, które nie są niezbędne do funkcjonowania strony, w szczególności zbierające dane osobiste do celów analitycznych, reklamowych i innych. Wymagają zgody użytkownika strony internetowej.
Ciasteczka statystyczne są używane do badania tego, jak użytkownicy zachowują się na stronie internetowej. Pomagają dostarczać informacje o wskaźnikach takich jak liczba odwiedzin na stronie, współczynnik odrzuceń, źródła odwiedzin itd.
Ciasteczka reklamowe są używane do celów marketingowych. Śledzą wizyty użytkowników na stronach internetowych i zbierają informacją o ich zachowaniach, aby docierać do nich z odpowiednimi reklamami.
Ciasteczka wydajnościowe używane są do zrozumienia i analizy kluczowych indeksów strony, takich jak szybkość wyświetlania treści, liczba wyświetleń video itp. Dzięki nim możemy poprawiać stronę tak, żeby korzystanie z niej było bardziej przyjazne dla użytkowników.
Ciasteczka funkcjonalne pomagają wykonywać określone funkcje, takie jak udostępnianie treści strony na platformach mediów społecznościowych, zbieranie opinii oraz inne funkcje stron trzecich.
Wynik to liczba
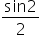

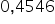
Czy mając udowodnioną nierówność
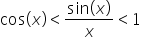

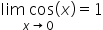

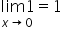

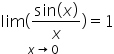
Według mnie, tak. Spełnione są założenia twierdzenia ale tylko dla x > 0, więc podobne rozumowanie trzeba by było przeprowadzić również dla x < 0.Pozdrawiam,Adam
tak e^1
Co do poprzedniego pytania to sobie poradziłam . Mam mały problem z granicą funkcji x dąży do minus nieskończoności (1+1/x)^x wydaje mi się że rozwiązaniem będzie liczba e ale nie wiem jak to zapisać
super strona !
Mam pytanie co jeżeli zamiast x dąży do zera będzie x dążący do nieskończoności ??
Wtedy oczywiście nie wyrażenie dazy do zera, gdyż sinx jest ograniczony przez 1 a x zbiega do nieskoczonosci 😉
Moglibyście trochę poprawić TeX’a. W wielu wypadkach używacie
sin x
zamiast
sin x
😉