Limit of the sinx/x function – proof

Limits of functions Lecture 8

Topic: Limit of a function \underset{x\rightarrow0}{\lim}\frac{sinx}{x}=1 – proof

Summary

In the article I will show proof that:

\underset{x\rightarrow0}{\lim}\frac{sinx}{x}=1

I didn’t come up with the proof myself, I just took it from GMFichtenholz’s book “Differential and Integral Calculus” (with a small modification at the very end) – of course extending it to include all transitions, for a better understanding of what comes from what. To demonstrate the above limit, I will use Cauchy’s definition of the limit of a function.

Demonstrating a certain inequality useful for proof

Lemma

For 0<x<\frac{1}{2} :

sinx<x i x<tgx .

Proof of the lemma

So we our task is to prove the inequality:

sinx< x< tgx, which occurs for 0< x< \frac{1}{2}

This inequality is worth remembering, because it is useful not only for this proof, but for various other things in mathematical analysis (for example, for estimating numerical series in a comparative convergence criterion). Besides, it’s interesting in itself, right? 🙂

Let’s go ahead and prove this inequality.

First, let’s draw something like this:

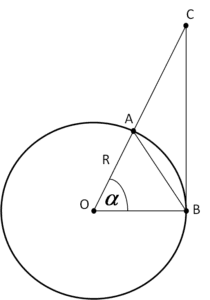We have a circle with center O, radius R, chord AB, angle AOB equal to \alpha , and tangent BC to the circle at point B.

Let’s note three things:

1. Area of ​​triangle OAB
2. Area of ​​a sector of a circle with angle \alpha AOB (do not confuse it with the triangle from point 1!)
3. Area of ​​triangle COB

It is obvious that always:

Area of ​​triangle OAB < AOB circle’s slice field < Area of ​​triangle COB

Now let’s compute these fields one by one:

1. Area of ​​triangle OAB

From high school we remember an alternative to the clichéd ” P=\frac{1}{2}ah ” formula:

Area of ​​a triangle = \frac{1}{2} side length times side length times sine of the angle between them.

In our particular triangle, both sides have length R (radius of the circle), so the area of ​​the triangle is:

P_{\Delta} OAB=\frac{1}{2}{R}^{2}sin{\alpha}

2. OAB slice field

The area of ​​the sector can be determined, for example, from proportions (or a ready-made formula – if you know it). The area of ​​the entire circle corresponds to the angle 2\pi (in radians), and the area of ​​the segment (which we are about to calculate) corresponds to the angle \alpha radians. The proportions will look like this:

{\pi}{R}^{2}  —  2\pi

P(AOB)  —  \alpha

therefore:

\frac{{\pi}{R}^{2}}{P(AOB)}=\frac{2\pi}{\alpha}

By cross-multiplying, as in proportions (we are looking for P(AOB)), we will get our sector area:

P(AOB)=\frac{{\pi} R^2{\alpha} }{2\pi} =\frac{R^2{\alpha} }{2}=\frac{1}{2}R^2{\alpha}

3. Area of ​​triangle COB

This triangle is a right triangle (because line CB is a tangent line). Therefore, we can assume that the segment OB (equal to R) is its base, and the segment CB – the height, and use the standard P = \frac{1}{2}ah formula.

P_{\Delta} COB=\frac{1}{2}|OB||CB|=\frac{1}{2}R|CB|

However, let’s include angle \alpha in this formula, instead of |CB| . We know that in this triangle:

tg{\alpha} =\frac{|CB|}{|OB|}=\frac{|CB|}{R}

Multiplying both sides of the equality by R we get:

|CB|=Rtg{\alpha}

…which we can substitute into the formula for the area of ​​triangle COB, obtaining:

P_{\Delta} COB=\frac{1}{2}|OB||CB|=\frac{1}{2}R\cdot{Rtg{\alpha}} =\frac{1}{2}R^2{tg{\alpha}}

In this way, we have all 3 areas from the picture above computed.

So now let’s go back to inequality:

Area of ​​triangle OAB < AOB slice field < Area of ​​triangle COB

Substituting the calculated fields we get:

\frac{1}{2}R^2 sin{\alpha}< \frac{1}{2}R^2{\alpha}< \frac{1}{2}R^2tg{\alpha}

We divide both sides by \frac{1}{2}R^2 (and we can do so, because the radius of the circle is greater than zero) and we get:

sin{\alpha}<{\alpha}< tg{\alpha}

And this is exactly the inequality we wanted to prove! And we have just proved this way 🙂

Conclusions from the proven inequality

So let’s start with the already proven inequality and transform it a bit:

sinx < x < tgx

First, let’s break it down into two ineqalities:

1. sinx < x

We divide it on both sides by x (we can, because x is assumed to be 0 < x < {pi}/2 – i.e. non-zero and positive, so the inequality sign will not change):

\frac{sinx}{x} < 1

2. x < tgx

As we know tgx=\frac{sinx}{cosx} :

x < \frac{sinx}{cosx}

After multiplying by cosx (we can, due to the assumption about x’s mentioned earlier):

xcosx < sinx

And divided by x (we can, due to the assumption about x):

cosx<\frac{sinx}{x}

So in this way, we have two inequalities transformed:

\frac{sinx}{x} < 1 cosx < \frac{sinx}{x}

Which we can combine and write:

cosx < \frac{sinx}{x} < 1

After subtracting 1 by both sides we get (if you are confused, you can break it down into two inequalities):

cosx-1 < \frac{sinx}{x}-1 < 0

We multiply both sides by -1 (this will change the inequality signs):

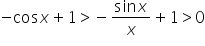
We write more neatly:

0 < 1-\frac{sinx}{x} < 1-cosx

At first, let’s deal with 1-cosx :

At the beginning, unfortunately, we must repeat a certain trigonometric formula, namely the formula for the cosine of a double angle:

cos2x=cos^2{x} -sin^2{x}

So (according to this formula):

cosx=cos^2(\frac{1}{2} x)-sin^2(\frac{1}{2} x)

That is:

1-cosx=1-(cos^2(\frac{1}{2} x)-sin^2(\frac{1}{2} x))

By using the “Pythagorean identity” I get from this:

1-cosx=cos^2(\frac{1}{2} x)+sin^2(\frac{1}{2} x)-cos^2(\frac{1}{2} x)+sin^2(\frac{1}{2} x)

That is:

1-cosx=2sin^2(\frac{1}{2} x)

So back to our inequality:

0 < 1-\frac{sinx}{x} < 1-cosx

We can write it as:

0 < 1-\frac{sinx}{x} < 2sin^2(\frac{1}{2} x)

Now let’s deal with 2sin^2(\frac{1}{2} x) .

It is true that:

2sin^2(\frac{1}{2} x) < 2sin(\frac{1}{2} x)

because for x it is assumed to be in the range 0 < x  < \frac{\pi}{2}, in which sine values ​​are fractions in the interval (0,1), and such squared fractions are smaller than before squared (for example \frac{1}{16} < \frac{1}{4}).

It is also true that:

2sin(\frac{1}{2} x) < x

because after dividing the inequality by 2 we get:

2sin(\frac{1}{2} x) < \frac{x}{2}

and we’ve already showed in the lemma that the sine of something is smaller than that something ( sinx < x < tgx ) at the beginning.

So going back to our main inequality:

0 < 1-\frac{sinx}{x} < 2sin^2 (\frac{1}{2} x)< 2sin(\frac{1}{2} x) < x

And making it shorter:

0 < 1-\frac{sinx}{x} < x

The above inequality results in the following inequality:

|1-\frac{sinx}{x} | < | x |

– the absolute value is the distance from zero, so it will not change when x changes to negative, as long as x remains between 0 and \frac{\pi}{2} .

Due to the fact that in absolute values ​​| a-b | = | b-a | :

| \frac{sinx}{x} - 1 | < | x |

Let us repeat, we have shown that the below inequality holds (for 0 < x < \frac{\pi}{2} ):

| \frac{sinx}{x} - 1 | < | x |

Cauchy definition of the limit of the function

Recall: if we want to prove from the Cauchy definition of the limit of the function that \underset{x\rightarrow0}{\lim}\frac{sinx}{x}=1 we have to show that we will always find one \delta that for every \epsilon the follow will occur:

0 < |x-0| < \delta\Rightarrow | \frac{sinx}{x} - 1| < \epsilon

That is:

0 < |x| < \delta\Rightarrow | \frac{sinx}{x} - 1| < \epsilon

Let’s start by acknowledge simple fact: if we choose just any \epsilon – indeed we can always find some \delta for it as a number greater than zero, less than epsilon and in the range 0 < \delta < \frac{\pi}{2} as well.

Next, from assumption 0 < |x| < \delta our x’s will be smaller than the delta, and since we showed earlier in the proof, that | \frac{sinx}{x}-1 | < | x | we conclude that:

| \frac{sinx}{x}-1 | < | x | < \delta < \epsilon

So in this way we have shown, that for any given \epsilon we can find \delta, that below is true :

| \frac{sinx}{x} -1 | < \epsilon

So we have shown from Cauchy’s definition that:

\underset{x\rightarrow0}{\lim}\frac{sinx}{x}=1

While writing this post, I used…

1. “Differential and integral calculus. Volume I.” GM Fichtenholz. Polish Ed. 1966.

END

Click to remind yourself how to apply limits of functions by definition (previous Lecture)< —

Click here to return to the Boundary Lectures page