Granica funkcji sinx/x – dowód

Granice funkcji Wykład 8

Temat: Granica funkcji   – dowód

Streszczenie

W artykule pokażę dowód na to, że:

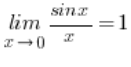
Dowodu nie wymyśliłem sam, tylko wziąłem z książki G.M.Fichtenholz’a “Rachunek różniczkowy i całkowy” (z małą przeróbką na samym końcu) – oczywiście rozszerzając o wszystkie przejścia, dla lepszego zrozumienia, co się bierze z czego. Do wykazania powyższej granicy wykorzystam definicję Cauchy’ego granicy funkcji.

Wykazanie pewnej pożytecznej dla dowodu nierówności

Lemat

Dla :

.

Dowód

Czyli wykażemy jakby nierówność:

, która zachodzi dla

Tą nierówność warto zapamiętać, przydaje się nie tylko do tego dowodu, ale do różnych innych rzeczy w analizie matematycznej (na przykład do szacowania szeregów liczbowych w kryterium porównawczym). Poza tym w ogóle jest ciekawa sama w sobie, prawda? 🙂

No to do dzieła, dowiedźmy tej nierówności.

Na początku narysujmy coś takiego:

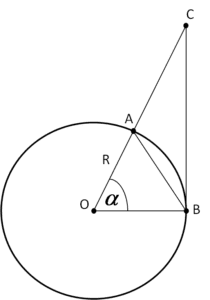Mamy okrąg o środku w punkcie O, promieniu R, cięciwie AB, kącie AOB równym i stycznej BC do okręgu w punkcie B.

Zwróćmy uwagę na trzy rzeczy:

1. Pole trójkąta OAB
2. Pole wycinka koła o kącie AOB (nie myl z trójkątem z punktu 1!)
3. Pole trójkąta COB

Oczywistym jest, że zawsze:

Pole trójkąta OAB < Pole wycinka AOB < Pole trójkąta COB

Teraz po kolei wyznaczmy te pola:

1. Pole trójkąta OAB

Ze szkoły średniej pamiętamy alternatywny wobec oklepanego “” wzór:

Pole trójkąta =  bok razy bok razy sinus kąta pomiędzy nimi.

W naszym konkretnym trójkącie oba boki mają długość R (promień koła), zatem pole trójkąta równe jest:

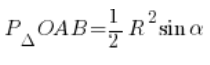
2. Pole wycinka OAB

Pole wycinka można wyznaczyć na przykład z proporcji (albo gotowym wzorkiem – jak się zna). Polu całego okręgu odpowiada kąt (w radianach), a polu wycinka (które mamy właśnie policzyć), kąt radianów. Proporcje wyglądać będą tak:

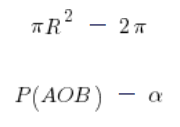
Mnożąc na krzyż, tak jak to się w proporcjach działało (szukamy P(AOB)) otrzymamy nasze pole wycinka:

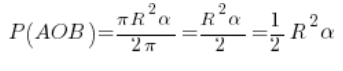
3. Pole trójkąta COB

Ten trójkąt jest trójkątem prostokątnym (bo prosta CB jest styczną). Zatem można przyjąć, że odcinek OB (równy R) to jego podstawa, a odcinek CB – wysokość i skorzystać ze standardowego .

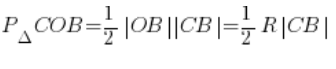
Zamieszajmy jednak do tego wzoru kąt , zamiast odcinka . Wiemy, że w tym trójkącie:

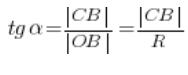
Mnożąc obie strony równości przez R otrzymamy:

…które możemy podstawić do wzoru na pole trójkąta COB, otrzymując:

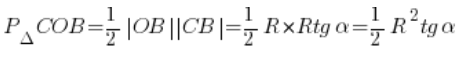
Mamy wyznaczone wszystkie 3 pola.

Wróćmy więc do nierówności:

Pole trójkąta OAB < Pole wycinka AOB < Pole trójkąta COB

Podstawiając wyliczone pola otrzymamy:

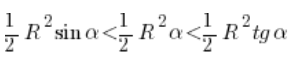
Dzielimy obustronnie przez (możemy, bo promień okręgu jest większy od zera) i otrzymujemy:

A jest to dokładnie nierówność, którą mieliśmy udowodnić! I udowodniliśmy sposób 🙂

Wnioski z udowodnionej nierówności

Wyjdźmy zatem z udowodnionej już nierówności i przekształćmy ją trochę:

Najpierw rozbijemy ja na dwie:

1.

Dzielimy ją obustronnie przez x (możemy, bo x z założenia jest 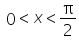 – czyli różne od zera i dodatnie, nie zmieni się więc znak nierówności):

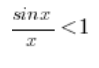
2.

Jak wiemy :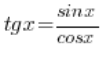

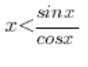
Po przemnożeniu przez cosx (możemy, ze względu na założenie dotyczące x-sów):

I podzieleniu przez x (możemy ze względu na założenie odnośnie x):

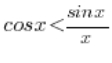
Mamy więc przekształcone dwie nierówności:

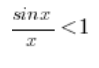
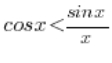
Które możemy połączyć i zapisać:

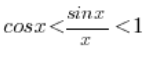
Odejmując stronami 1 otrzymamy (jeśli chcesz, możesz to rozpisać z rozbiciem na dwie nierówności):

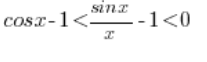
Mnożymy stronami przez -1 (zmieni to znaki nierówności):

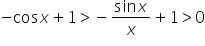
Zapisujemy zgrabniej:

Zajmijmy się :

Na początku powtórzyć musimy sobie niestety pewien wzór trygonometryczny, mianowicie wzór na cosinus podwojonego kąta:

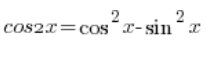
A więc (z tego wzoru):

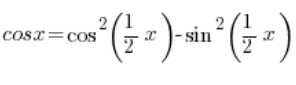
Czyli:

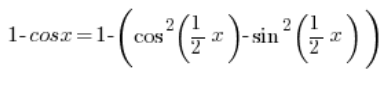
Rozbijając jedynkę z jedynki trygonometrycznej i wchodząc z minusem w nawias otrzymam:

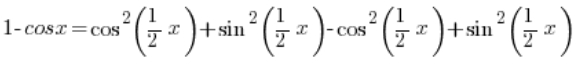
Czyli:

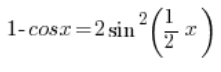
Wracając więc do naszej nierówności:

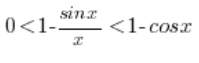
Możemy ją zapisać jako:

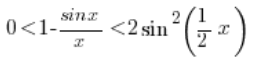
Zajmijmy się teraz .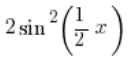

Jest prawdą, że:

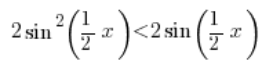
bo dla x z założenia z przedziału 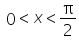wartości sinusa są ułamkami z przedziału (0,1), a takie ułamki podniesione do kwadratu są mniejsze niż przed podniesieniem (na przykład ).

Jest także prawdą, że:

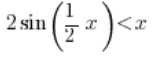
bo po podzieleniu nierówności przez 2 otrzymamy:

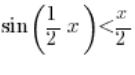
a to, że sinus z czegoś jest mniejszy od tego czegoś wykazaliśmy w lemacie () na początku.

Zatem wracając do naszej głównej nierówności:

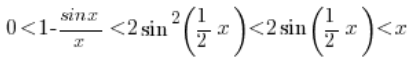
Skracając:

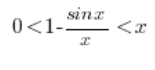
Z powyższej nierówności wynika poniższa:

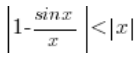
– wartość bezwzględna to odległość od zera, zatem nie zmieni się ona przy zmianie znaku x na ujemny, dopóki oczywiście x pozostaje pomiędzy 0 a .

Ze względu na to, że w wartościach bezwzględnych :

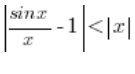
Powtórzmy, wykazaliśmy, że zachodzi nierówność (dla ).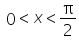

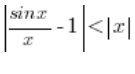
Definicja granicy funkcji Cauchy’ego

Przypomnijmy: jeśli chcemy wykazać z definicji granicy funkcji Cauchy’ego, że 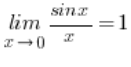 musimy pokazać, że zawsze znajdziemy takie , że dla dowolnego zachodzić będzie:

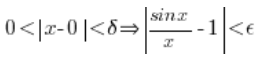
Czyli:

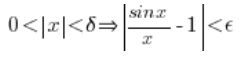
Sprawa jest więc prosta: jeżeli obierzemy sobie byle jaki – zawsze możemy dobrać do niego takie jako liczbę większą od zera, mniejszą od epsilona i należącą do przedziału .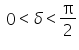

Z nierówności nasze x-sy będą mniejsze od delty, a skoro pokazaliśmy wcześniej, że 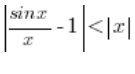  to prawdą jest, że:

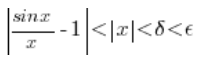
Czyli wykazaliśmy, dla takiej :

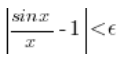
Pokazaliśmy więc z definicji Cauchy’ego, że:

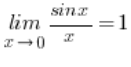
Pisząc tego posta korzystałem z…

1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.

KONIEC

Kliknij, aby przypomnieć sobie, jak stosować granice funkcji z definicji (poprzedni Wykład) <–

Kliknij, aby powrócić na stronę z wykładami o granicach