No hay productos en el carrito.
Krystian Karczyński- 18 abril 2024
- Komentarz 0
Al resolver problemas con ecuaciones polinómicas complejas, generalmente usamos los mismos métodos que en las ecuaciones polinómicas reales en la escuela secundaria.
Ecuaciones complejas de cuarto grado reducibles a segundo grado
Esto también se aplica a las ecuaciones complejas de cuarto grado que se pueden reducir a ecuaciones de segundo grado, es decir, aquellas en las que tenemos una variable a la cuarta potencia, a la segunda potencia y un término constante, por ejemplo:
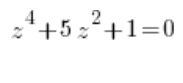
o:
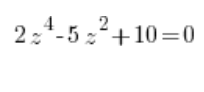
Reducimos este tipo de ecuaciones complejas a ecuaciones complejas de segundo grado mediante la sustitución de 
, donde 
es obviamente la variable compleja.
Tarea
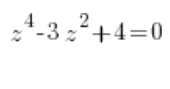
Sustituimos (por supuesto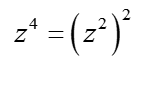 
), así obtenemos:
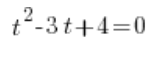
Y así resolvemos esta ecuación de la manera habitual usando el discriminante (por supuesto, las raíces de números negativos existen en los números complejos). Obtendremos dos soluciones complejas:
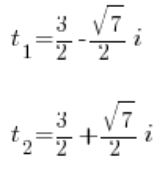
Dado que sustituimos: , tenemos:
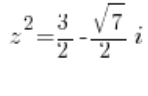
o:
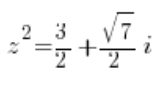
es decir:
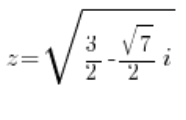
o:
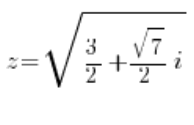
Después de calcular las raíces (por supuesto, saldrán cuatro raíces complejas), tendremos cuatro soluciones:
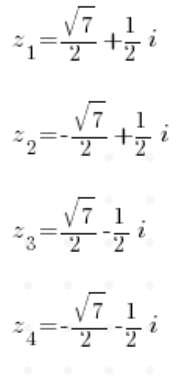
P.D. Muestro este y otros métodos en la Lección 6 de mi Curso de Números Complejos, ¡visítalo!
