Sistema de Ecuaciones con un Parámetro a Determinar
Krystian Karczyński
Fundador y jefe del servicio eTrapez.
Maestro en Matemáticas por la Universidad Tecnológica de Poznań (Polonia). Tutor de matemáticas con muchos años de experiencia. Creador de los primeros Cursos eTrapez, que se han vuelto enormemente populares entre estudiantes de toda Polonia.
Vive en Szczecin (Polonia). Le gusta caminar por el bosque, ir a la playa y hacer kayak.
Calcula el parámetro ‘a’ en el sistema de ecuaciones anterior, sabiendo que es inconsistente.
En lugar de comenzar sistemáticamente calculando el rango de la matriz principal, determinemos el rango de la matriz aumentada:
…es igual a dos porque en esta matriz puedes extraer un determinante de segundo orden no nulo (y no puedes obtener uno más grande):
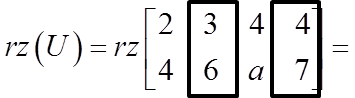
Entonces, el rango de la matriz aumentada es igual a 2.
Aplicación del Teorema de Kronecker-Capelli
¿Cuál debería ser el rango de la matriz principal?
Sabemos que el sistema es inconsistente, y del Teorema de Kronecker-Capelli sabemos que será inconsistente cuando el rango de la matriz principal sea diferente al rango de la matriz aumentada. También sabemos que el rango de la matriz principal siempre es menor o igual al rango de la matriz aumentada (la matriz principal está contenida en la aumentada). Entonces, el rango de la matriz principal debería ser 1 o 0 (para ser diferente al rango de la matriz aumentada).
El rango de la matriz principal será:
Vemos que definitivamente no será 0 (solo la matriz nula tiene un rango de 0) – por lo tanto, debería ser 1. El rango será uno cuando la primera y segunda filas sean proporcionales (entonces eliminaremos una de ellas). Vemos que la primera fila multiplicada por dos da la segunda fila, si solo a es igual a 8.
Así que rápidamente y sin grandes cálculos llegamos a la respuesta:
¿Buscas clases particulares de matemáticas para nivel universitario o de secundaria? ¿O quizás necesitas un curso que te prepare para el examen de selectividad?
Somos el equipo de eTrapez. Enseñamos matemáticas de manera clara, sencilla y muy detallada - llegamos incluso al más resistente al aprendizaje.
Hemos creado cursos en video explicados en un lenguaje comprensible para descargar en tu computadora, tableta o teléfono. Enciendes la grabación, miras y escuchas, como en las clases particulares. A cualquier hora del día o de la noche.
