Definición del rango de una matriz y sus implicaciones
Supongamos que hemos definido el rango de una matriz como: «el número de filas y columnas linealmente independientes en una matriz». ¿Qué propiedades del rango se derivan de esta definición desde el principio?
Primero, es obvio que el rango de una matriz puede ser: 1, o 4, o a veces 0. Pero definitivamente no será: -4, o ![]() .
.
¿Vale, eso es todo?
Pero, ¿eso es todo lo que se puede obtener? Tomemos, por ejemplo, la matriz:
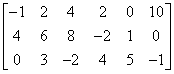
Esta matriz tiene 3 filas y 6 columnas.
Preguntémonos, ¿cuál puede ser el rango de esta matriz? ¿Puede ser igual a 7? Está claro que no, porque si el rango de una matriz es «el número de filas y columnas linealmente independientes», no puede ser 7 en este caso porque esta matriz no tiene tantas filas ni tantas columnas.
Ahora una pregunta más difícil… ¿Puede el rango ser igual a 6? La matriz tiene 6 columnas…
La respuesta es: no. 6 tendría que ser «el número de filas y columnas linealmente independientes». 6 puede ser el número de columnas linealmente independientes (porque hay 6), pero no puede ser el número de filas linealmente independientes (porque solo hay 3). Y debería ser el número de «filas y columnas» linealmente independientes.
Así que, es obvio que el rango de esta matriz puede ser como máximo 3.
Llegamos a una propiedad útil:
rango(A) <= min(número de filas de la matriz, número de columnas de la matriz)
Por lo tanto, al observar una matriz, puedes decir inmediatamente cuál es su rango máximo – lo que a veces puede ser muy útil.
Para calcularlo con más precisión, necesitas usar métodos apropiados – los muestro en mi Curso de Matrices en la Lección 5, ¡bienvenido!


