Para responder a la pregunta planteada en el título, no necesitamos retroceder hasta la definición de una asíntota oblicua, solo necesitamos saber qué es una función.
Como a menudo ocurre en matemáticas, imaginemos temporalmente que el gráfico de la función TIENE dos asíntotas oblicuas diferentes en 
y demostremos que al asumir esto, llegaremos a una contradicción, por lo tanto, esta suposición no puede ser aceptada.
Gráfico
En el gráfico, estas asíntotas podrían verse así:
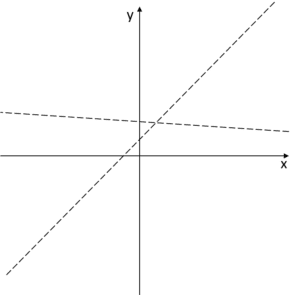Y el gráfico de la función debería acercarse a estas asíntotas en , por lo tanto, se vería de la siguiente manera:
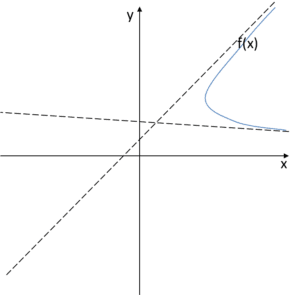¿Y qué? ¿Puede ser así? ¿Puede el gráfico de una función verse así? ¿O tenemos aquí algún problema?
Problema
Obviamente, tenemos un problema. Lo que se muestra arriba no puede ser el gráfico de una función. Volvamos a la definición, una función por definición es una asignación que asigna a cada argumento x exactamente un valor y. ¿Qué se desprende de nuestro gráfico?
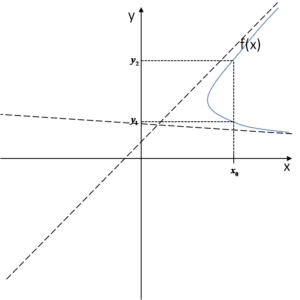Se puede leer de él que, por ejemplo, al argumento 
se le asignan dos valores – 
y 
. Y eso no puede ser en un gráfico de función, porque en ella cada argumento x debe corresponder a solo un valor y.
Por lo tanto, una función no puede tener dos asíntotas oblicuas diferentes en . Todo el razonamiento se puede repetir adecuadamente para 
🙂
