Recibo muchas preguntas sobre la fórmula de la forma canónica de una función cuadrática que introduje en el Curso de Integrales Indefinidas.
La fórmula:
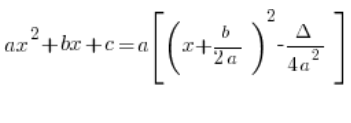
aparece en el esquema para resolver integrales racionales en la Lección 5 del curso:
Esquema para integrales racionales
¿Por qué está ahí a^2?
El problema es que a primera vista, parece diferente de la forma canónica conocida de la escuela secundaria:
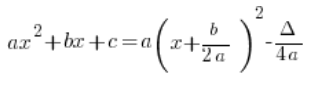
La pregunta estándar aquí es: «¿Por qué tiene 
en el denominador?»
Transformación de la fórmula
Basta con notar que si en la fórmula:
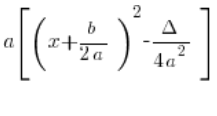
multiplicamos 
por el corchete cuadrado, obtenemos exactamente la fórmula:
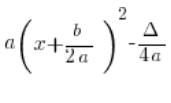
(después de multiplicar por el término 
, se cancela y obtenemos 
)
Por lo tanto, ambas formas son equivalentes, es decir, simplemente:
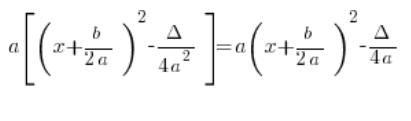
Entonces, ¿por qué introducir esta fórmula con el corchete cuadrado y a fuera del corchete? Porque en las integrales racionales es más conveniente 🙂
En las etapas posteriores del cálculo de la integral, aún necesitarás extraer antes del signo de la integral (y primero antes del corchete en el denominador), ¿por qué esperar? 🙂
