No hay productos en el carrito.
Krystian Karczyński- 5 agosto 2024
- Komentarz 0
Reducir algunas ecuaciones de cuarto grado a ecuaciones cuadráticas
Muchas ecuaciones polinómicas de cuarto grado se pueden transformar en ecuaciones cuadráticas utilizando un truco bien conocido de la escuela secundaria que se describe aquí:
Reducir a una ecuación cuadrática
Esto funciona, por supuesto, y de la mejor manera también para polinomios en números complejos.
Para recordarte, teniendo la ecuación:
{{z}^{4}}+3{{z}^{2}}+2=0Sustituimos: {{z}^{2}}=t
Y obtenemos una ecuación cuadrática:
{{t}^{2}}+3{t}+2=0Luego la resolvemos usando delta común y así sucesivamente, tenemos soluciones 
, recordando que 
formamos dos ecuaciones adicionales a partir de ellas:
o 
Las resolvemos y tenemos cuatro soluciones: 
.
Reducir algunas ecuaciones de grados mayores a ecuaciones cuadráticas
Absolutamente nada impide extender este método a ecuaciones de grados mayores que 4 (si, por supuesto, se pueden reducir a cuadráticas mediante sustitución).
Así que tenemos:
2{{z}^{6}}-5{{z}^{3}}+4=0También se puede notar que es equivalente a:
2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0Y después de sustituir: 
Obtenemos una cuadrática:
2{{t}^{2}}-5t+4=0En la ecuación:
{{x}^{10}}-3{{x}^{5}}+1=0Después de sustituir: 
Tenemos:
{{t}^{2}}-3t+1=0Y así sucesivamente, y así sucesivamente…
Ejemplo
Tomemos la ecuación:
z^6+(1-i)z^3-i=0Sustituimos z^2=t y tenemos:
t^2+(1-i)t-i=0Luego calculamos:
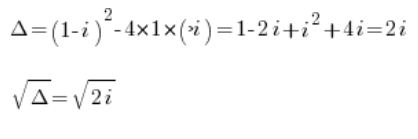
Calculamos estas raíces utilizando los métodos conocidos de números complejos (mostrados por ejemplo en mi Curso).
Tenemos 
o 
Es decir:
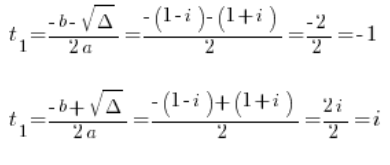
Recordando que estos no son aún soluciones, porque z^3=t
Así que tenemos que resolver las ecuaciones:
z^3=-1Y:
z^3=iLas transformamos en:
y 
Y calculando nuevamente utilizando los métodos conocidos, tenemos tres raíces de la primera ecuación:
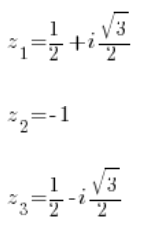
Y tres raíces de la segunda ecuación:
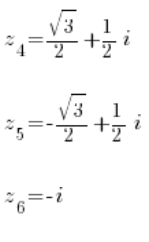
Resuelto 🙂
