Funciones Ciclométricas (Conferencia)
Tema: Funciones ciclométricas
Resumen
En esta conferencia, presentaré el concepto de funciones ciclométricas: arcsinx, arccosx, arctgx, arcctgx. Estas son las funciones inversas de las funciones trigonométricas.
La conferencia consta de dos partes. En la primera parte, solo muestro cómo calcular rápidamente los valores de las funciones ciclométricas, sin profundizar demasiado en el tema (a esta parte se adjunta un video, fragmento de mi Curso de Cálculo Integral).
En la segunda parte, describo las funciones ciclométricas con más detalle, mostrando sus gráficas, etc.
Para entender la conferencia, necesitarás:
- funciones trigonométricas (nivel de secundaria)
Parte I
Funciones ciclométricas – Versión «INSTANTÁNEA»
Las funciones ciclométricas en términos sencillos son simplemente las funciones inversas de las trigonométricas. Es decir, arcsinx es la función inversa de sinx.
Entonces, si sabemos, por ejemplo, que 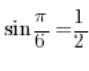 , significa que
, significa que ![]() .
.
Y así sucesivamente:
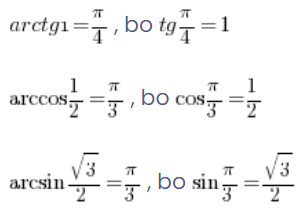
Además, tenemos algunas propiedades de las funciones ciclométricas que nos permiten calcular sus valores incluso para argumentos negativos:
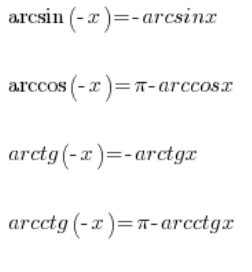
Así que también podemos calcular esto:
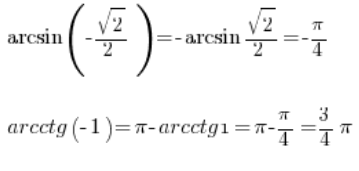
Entonces, teniendo una tabla de funciones trigonométricas podemos determinar fácilmente los valores de las funciones ciclométricas, simplemente leyéndola «al revés».
Lo explico más detalladamente en el video aquí:
Tabla de valores básicos de las funciones trigonométricas del video – descargar aquí.
Parte II
Funciones ciclométricas – Versión Completa
Introducción – Por qué la Parte I no es suficiente
Parece que en la Parte I definimos cada función ciclométrica como la inversa de la función trigonométrica correspondiente.
Formalicemos esto un poco. Dijimos que, por ejemplo, la función ![]() toma el valor
toma el valor ![]() , cuando la función
, cuando la función ![]() de este
de este ![]() es igual a
es igual a ![]() .
.
Correspondientemente:
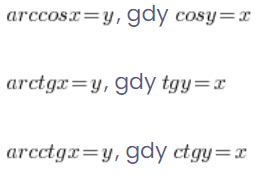
Entonces, si queremos calcular ![]() , nos preguntamos cuál es el coseno de qué ángulo da
, nos preguntamos cuál es el coseno de qué ángulo da ![]() , nos damos cuenta de que es el ángulo
, nos damos cuenta de que es el ángulo ![]() y tenemos el resultado:
y tenemos el resultado: 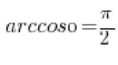 .
.
¿Esto cubre todos los valores de las funciones ciclométricas?
Por supuesto que NO.
Repasemos todo el razonamiento con números específicos (y tal vez pasemos tradicionalmente a arcsinx):
Si queremos calcular  , nos preguntamos cuál es el seno de qué ángulo da
, nos preguntamos cuál es el seno de qué ángulo da ![]() , nos damos cuenta de que es el ángulo
, nos damos cuenta de que es el ángulo ![]() y tenemos el resultado:
y tenemos el resultado:  .
.
¿Dónde está el problema? En la parte en negrita:
Si queremos calcular  , nos preguntamos cuál es el seno de qué ángulo da
, nos preguntamos cuál es el seno de qué ángulo da ![]() , nos damos cuenta de que es el ángulo
, nos damos cuenta de que es el ángulo ![]() y tenemos el resultado:
y tenemos el resultado:  .
.
Desafortunadamente, no solo el seno de ![]() es igual a
es igual a ![]() .
.
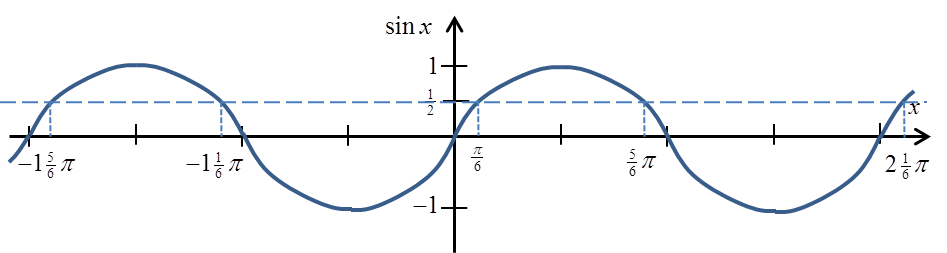
Recordemos el gráfico de sinx (he marcado el valor ![]() en él):
en él):
Podemos ver y ya sabemos desde la secundaria, que el seno toma el valor ![]() no solo para el ángulo
no solo para el ángulo ![]() , sino también para los ángulos:
, sino también para los ángulos: 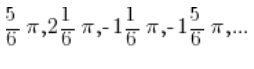
Entonces 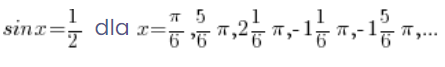
Recordemos nuevamente nuestro método para calcular arcsin:
Si queremos calcular  , nos preguntamos cuál es el seno de qué ángulo da
, nos preguntamos cuál es el seno de qué ángulo da ![]() , nos damos cuenta de que es el ángulo
, nos damos cuenta de que es el ángulo ![]() y tenemos el resultado:
y tenemos el resultado:  .
.
Pero ahora sabemos que no solo sin![]() da
da ![]() , por lo que parece que:
, por lo que parece que:
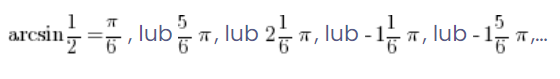
Esto significaría que arcsinx no es una función en absoluto, ¡porque un argumento tiene varios valores asignados!
Dar una respuesta clara a la pregunta de cuánto es el arcsin de algo sería completamente imposible.
También es fácil imaginar que un problema similar se aplica a CUALQUIERA de las funciones trigonométricas.
Dicho de manera más profesional: estas funciones no son inyectivas, por lo que no existen funciones inversas para ellas. En cada una de las funciones trigonométricas, cada valor se alcanza para un número infinito de argumentos (son periódicas, ¿verdad?), por lo que al intentar determinar sus funciones inversas, obtendremos un número infinito de valores asignados a cada argumento. Y eso no puede ser en funciones.
¿Qué hacer?
Es bastante simple, por no decir primitivo. Cada una de las funciones trigonométricas puede RECORTARSE para obtener una función inyectiva.
Entonces, definamos correctamente las 4 funciones ciclométricas:
arcsinx
Recordemos el gráfico de la función sinx:
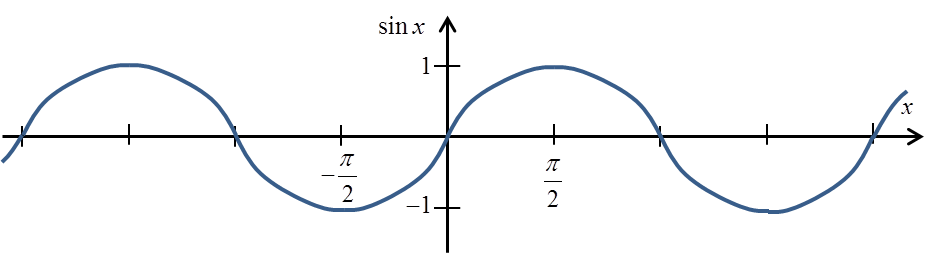
Si acordamos recortarlo, por ejemplo, al intervalo ![]() , obtenemos un gráfico así:
, obtenemos un gráfico así:
![Wykres sinx w przedziale [0,pi] Obraz3](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz33.png)
Desafortunadamente, esto no es lo que queremos, porque todavía no es el gráfico de una función inyectiva, y el problema con el valor de ![]() todavía existe:
todavía existe:
![Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2 Wykres funkcji sinx w przedziale [0,pi] z zaznaczoną wartością 1/2](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz41.png)
Entonces acordamos recortar la función sinx de manera diferente, a los argumentos 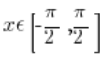 :
:
![Wykres funkcji sinx dla x należących do [-pi/2,pi/2] Wykres funkcji sinx dla x należących do [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz51.png)
Ahora es una función inyectiva y tiene una función inversa arcsinx.
El gráfico de la función arcsinx se verá más o menos así:

Su dominio es el intervalo ![]() .
.
La definición estricta de la función arcsinx es así:
![]() .
.
arccosx
La función cosx tampoco es inyectiva:
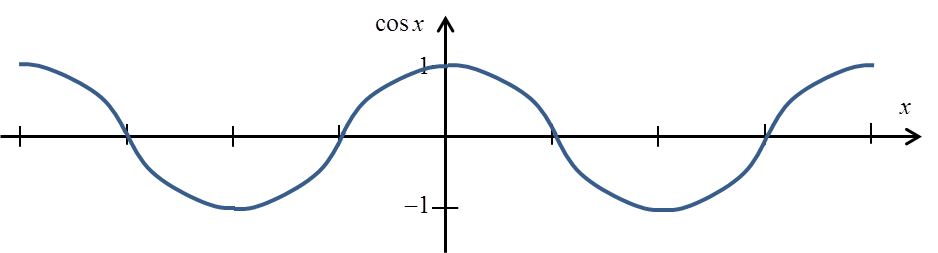
Para obtener una función inyectiva debemos recortarla al intervalo ![]() :
:
![Wykres funkcji cosx obciętej do przedziału [0,pi] Wykres funkcji cosx obciętej do przedziału [0,pi]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz8.png)
Así definida, la función ya es inyectiva y tiene una función inversa arccosx.
Su gráfico será aproximadamente:
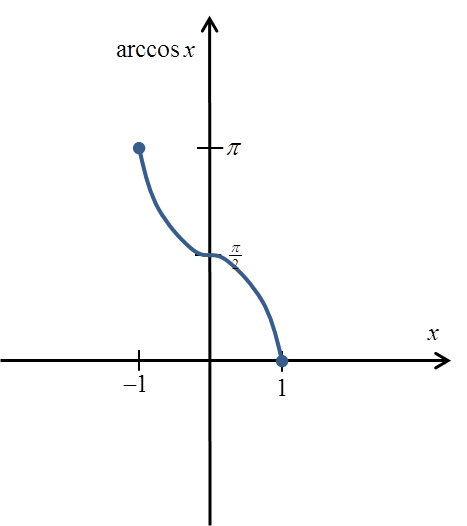
Y su definición estricta:
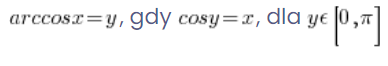 .
.
arctgx
El gráfico de la función tgx se ve así:

¡Tampoco es una función inyectiva! Podemos recortarla de la siguiente manera:
![Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2] Wykres funkcji tgx obięty do przedziału [-pi/2,pi/2]](https://blog.etrapez.pl/wp-content/uploads/sites/3/2012/01/Obraz111.png)
Obteniendo así una función inyectiva.
El gráfico de la función arctgx se ve así:

Y su definición estricta es:
![]() , para y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
, para y\in \left( -\frac{\pi }{2},\frac{\pi }{2} \right).
También notamos que del gráfico se derivan algunas propiedades interesantes, por ejemplo:
- el dominio de la función arctgx es todo el conjunto de números reales (podemos calcular arctg de cualquier número)


arcctgx
Del gráfico de la función ctgx:

Cortamos una pieza inyectiva:
El gráfico de la función arcctgx se ve así:
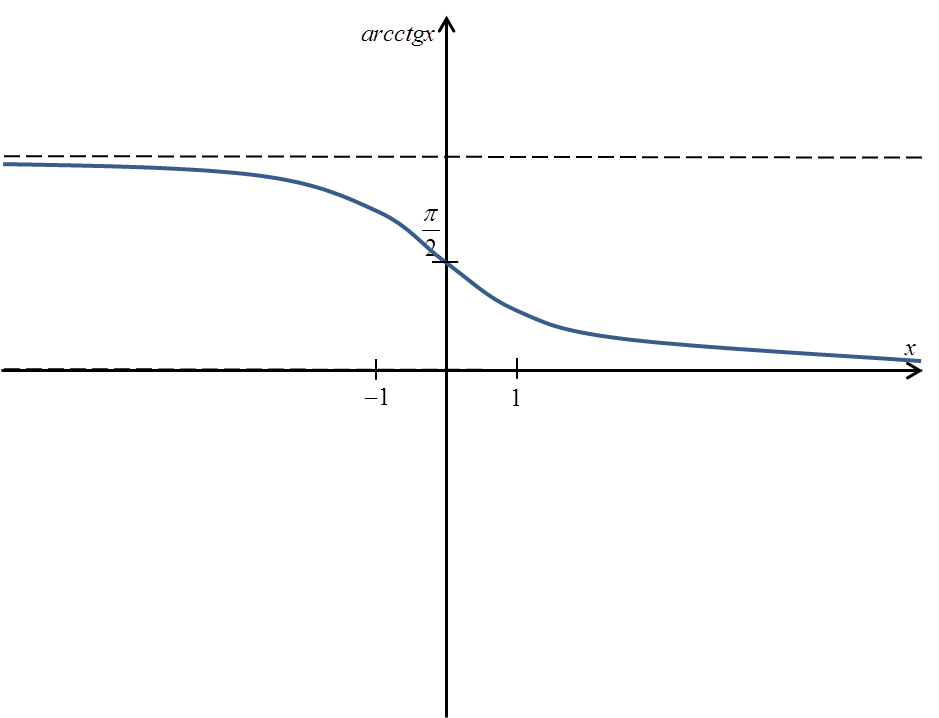
La definición estricta de arcctgx sería:
![]() .
.
Vemos que:
- el dominio de la función arcctgx es todo el conjunto de números reales (podemos calcular arcctg de cualquier número)


Nota
En muchas calculadoras y en la notación matemática en general (especialmente occidental), las funciones trigonométricas inversas no se denotan como «arcus,» sino con el exponente -1. Por ejemplo, arcsinx se escribe como ![]() . Si sabes de qué se trata, no hay problema. Sin embargo, puedes cometer un error terrible y confundir la función inversa de sinx con la función
. Si sabes de qué se trata, no hay problema. Sin embargo, puedes cometer un error terrible y confundir la función inversa de sinx con la función ![]() , que es una función completamente diferente de arcsinx.
, que es una función completamente diferente de arcsinx.