Cuantificadores – pero en realidad no estaban allí…
Bueno, no estoy 100% seguro de si los cuantificadores todavía están en la escuela secundaria después de los recortes regulares anuales de material. Realmente tampoco quiero comprobarlo porque, ¿para qué molestarse?
Deberían estar en el perfil ampliado. Realmente deberían.
Bueno, ¿pero quién necesita esto?
En la mayoría de las definiciones y teoremas matemáticos, se utilizan conceptos como: «cada» y «existe».
Más a menudo en algunas secuencias más complejas, por ejemplo: «entre cada dos números hay infinitos números» (esto es algo semiformal e inexacto), o: «para cada número real no negativo existe exactamente una raíz», o: «existe algo tal que para cada otra cosa existe otra cosa» (esta es la definición matemática de otra cosa).
En la universidad, recibirás una gran cantidad de definiciones y teoremas dados de esta manera, dictados rápidamente y en secuencia durante una conferencia, o – peor aún – escritos directamente en la pizarra en forma de:
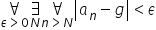
Así que sería bueno (en lugar de levantar la mano y preguntar al profesor si debes «redibujar» eso), que ya hayas aprendido a leer correctamente tales fórmulas. Podrías entonces pasar directamente a las etapas de «profundizar» en la definición, hacer algunas observaciones sobre «cómo funciona» en ejemplos concretos, etc.
Cuantificador general y específico – Conozcámonos mejor
«cada», «para cada» – este es un cuantificador general, denotado como: ![]() .
.
«existe», «existe tal» – este es un cuantificador específico, denotado como: ![]() .
.
Uso y recomiendo estos símbolos particulares de cuantificadores porque definitivamente no se confundirán entre sí.
![]() – es una A mayúscula invertida (del inglés «all» – cada).
– es una A mayúscula invertida (del inglés «all» – cada).
![]() – es una E mayúscula invertida (del inglés «exists» – existe).
– es una E mayúscula invertida (del inglés «exists» – existe).
También hay otros símbolos para los cuantificadores: Λ («para cada») y V («existe») – pero no voy a tratar con ellos porque confunden a todos.
Fórmulas matemáticas escritas usando cuantificadores
Las fórmulas más simples son de la forma:
![]() – leemos: «para cada x» (también se puede escribir como:
– leemos: «para cada x» (también se puede escribir como: ![]() , pero se confunde de nuevo, así que no lo haré)
, pero se confunde de nuevo, así que no lo haré)
![]() – leemos: «existe x»
– leemos: «existe x»
Sin embargo, en general, las fórmulas son más complicadas, por ejemplo:
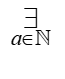 – leemos: «existe a que es un número natural», o: «existe tal a, perteneciente a los números naturales», o cualquier otra expresión en español, reflejando la esencia del asunto, es decir:
– leemos: «existe a que es un número natural», o: «existe tal a, perteneciente a los números naturales», o cualquier otra expresión en español, reflejando la esencia del asunto, es decir:
1. Existe a
2. a es un número natural
Aquí no hay reglas de lenguaje «rígidas» sobre lo que debe ser cada palabra y si debe ser «existe a» o debe ser «existe tal a».
Las fórmulas pueden y generalmente deben combinarse entre sí, por ejemplo:
\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,significa:
«para cada x>4, existe un n perteneciente a los números naturales»
Entendemos por esto que para cada x>4 «encontraremos» un n perteneciente a los números naturales, de modo que para cada x tal elegiremos el n apropiado. Los cuantificadores están lógicamente relacionados entre sí, no son dos fórmulas independientes escritas una al lado de la otra.
Además…
El orden importa
La misma fórmula que la última, pero con el orden de los cuantificadores invertido:
\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,…la leeremos de manera diferente:
«existe a que es un número natural, de modo que para x mayores que 4…»
Entendemos que primero tenemos algún n (del que sabemos que existe) y solo para este n específico sucede algo para todos los x>4.
Ejemplo – Digresión
Un ejemplo clásico aquí es la definición de convergencia uniforme y puntual de una secuencia de funciones, que difieren solo por… el orden de los cuantificadores (simplifiqué un poco estas definiciones):
Convergencia puntual:

Convergencia uniforme:

En la definición de convergencia uniforme, el cuantificador que estaba al principio de la puntual termina al final. Sin entrar en detalles, esto cambia el significado de toda la fórmula.
En la convergencia puntual, PRIMERO (leemos de izquierda a derecha) tomábamos algún x arbitrario, luego leyendo la fórmula llegábamos a la conclusión de que para este x establecido inicialmente las distancias entre los valores de las funciones en la secuencia y la función «límite» disminuyen hacia el infinito.
En la convergencia uniforme, PRIMERO determinábamos que la distancia entre los valores de las funciones apropiadas disminuye hacia el infinito, y luego llegábamos a la conclusión de que esto sucede para cualquier x.
Escritura de definiciones y teoremas
Sabiendo cómo leer los cuantificadores, la escritura de definiciones y teoremas matemáticos ya está abierta para nosotros. Por ejemplo:
\underset{x\in\mathbb{R}}{\mathop{\forall }}\,{{x}^{2}}\ge 0Lo leeremos como: «Para cada número real x, x al cuadrado es mayor o igual a cero», o más bonito: «Cada número x elevado al cuadrado es no negativo» – Definitivamente estoy a favor de leer definiciones y teoremas en un lenguaje más colorido.
La oración anterior es VERDADERA. No tenemos ningún problema en escribir también oraciones FALSAS:
\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1Lo leeríamos como: «Existe un número positivo a, de modo que para cada número x mayor que este a, a dividido por x es mayor que 1», lo cual es obviamente FALSO (porque un número positivo dividido por uno mayor que él nunca será mayor que 1 y no existe tal número).
Y ahora tomando la definición del límite de una secuencia del post anterior:

Lo leeremos así (agregando algunas explicaciones):
«Para cualquier ![]() mayor que cero, encontraremos un número de término de la secuencia
mayor que cero, encontraremos un número de término de la secuencia ![]() , de modo que para cada término de la secuencia
, de modo que para cada término de la secuencia ![]() con un número mayor que
con un número mayor que ![]() la distancia (el valor absoluto es la distancia) entre este término de la secuencia y el límite
la distancia (el valor absoluto es la distancia) entre este término de la secuencia y el límite ![]() será menor que
será menor que ![]() »
»
También podemos usar un lenguaje más humano:
«No importa cuán pequeña sea la distancia ![]() al principio, encontraremos un número de término de la secuencia, de modo que todos los términos posteriores de esta secuencia estarán más cerca del límite
al principio, encontraremos un número de término de la secuencia, de modo que todos los términos posteriores de esta secuencia estarán más cerca del límite ![]() que la distancia inicialmente establecida
que la distancia inicialmente establecida ![]() »
»