A Few Things You Should Have Learned Well in Middle School, But No One Told You – Part 2: Quantifiers

---

Quantifiers – but they weren’t really there…

Alright, I’m not 100% sure if quantifiers are still in high school after regular annual material cuts. I don’t really want to check either because why get upset.

They should still be in the extended profile. They really should.

Alright, but who needs this?

In most mathematical definitions and theorems, concepts like: “every” and “exists” are used.

Most often in some more complex sequences, for example, “between every two numbers, there are infinitely many numbers” (this is somewhat semi-formal and inaccurate), or: “for every non-negative real number, there exists exactly one root”, or: “there exists something-something, that for every something-else-something there exists another something-something” (this is the mathematical definition of another-something).

In college, you will get a whole heap of definitions and theorems given this way, dictated quickly and in sequence during a lecture, or – worse – written directly on the board in the form:

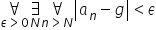
So it would be good (instead of raising your hand and asking the professor if you should “redraw” it) to have already learned how to read such formulas correctly. You could then go straight to the stages of “digging into” the definition, making a few observations on how it works with specific examples, etc.

General and Specific Quantifiers – Let’s Get to Know Them Better

“every”, “for every” – this is a general quantifier, denoted as: .

“exists”, “there exists” – this is a specific quantifier, denoted as: .

I use and recommend these particular quantifier symbols because they definitely won’t get mixed up.

– is an inverted capital A (from the English “all” – every).

– is an inverted capital E (from the English “exists” – exists).

There are also other symbols for quantifiers: Λ (“for every”) and V (“exists”) – but I’m not going to deal with these because they confuse everyone.

Mathematical Formulas Written Using Quantifiers

The simplest formulas are of the form:

– we read: “for every x” (can also be written as: , but it gets confused again, so I won’t do it)

– we read: “there exists x”

However, generally, formulas are more complicated, for example:

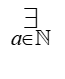– we read: “there exists a being a natural number”, or: “there exists such an a, belonging to the natural numbers”, or any other expression in English, reflecting the essence of the matter, namely that:

1. There exists a

2. a is a natural number

There are no “rigid” language rules here about what each word must be and whether it must be “there exists a” or it must be “there exists such an a”.

Formulas can and usually have to be combined with each other, for example:

\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,

means:

“for every x>4, there exists an n belonging to the natural numbers”

We understand by this that for every x>4 “we will find” an n belonging to the natural numbers, so for each such x we “choose” the appropriate n. Quantifiers are logically related to each other, not two independent formulas written next to each other.

Moreover…

Order Matters

The same formula as the last one, but with the order of quantifiers switched:

\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,

…we will read differently:

“there exists an a being a natural number, such that for x greater than 4…”

We understand that first we have some n (which we know exists) and only for this specific n something happens for all x>4.

Example – Digression

A classic example here is the definition of uniform and pointwise convergence of a sequence of functions, which differ only by… the order of the quantifiers (I simplified these definitions a bit):

Pointwise convergence:

Uniform convergence:

In the definition of uniform convergence, the quantifier that was at the beginning of pointwise ends up at the end. Without going into details, this changes the meaning of the whole formula.

In pointwise convergence, FIRST (we read from the left) we took some arbitrary x, then reading the formula we came to the conclusion that for this initially established x the distances between the values of the functions in the sequence and the “limit” function decrease to infinity.

In uniform convergence, FIRST we determined that the distance between the values of the appropriate functions decreases to infinity, and then we came to the conclusion that this happens for any x.

Writing Definitions, Theorems

Knowing how to read quantifiers, the writing of mathematical definitions and theorems is already open to us. For example:

\underset{x\in\mathbb{R}}{\mathop{\forall }}\,{{x}^{2}}\ge 0

We will read it as: “For every real number x, x squared is greater than or equal to zero”, or more nicely: “Every number x raised to the power of two is non-negative” – I am definitely in favor of reading definitions and theorems in a more colorful language.

The above sentence is TRUE. We have no problem writing FALSE sentences as well:

\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1

Which we would read as: “There exists a positive number a, such that for every number x greater than this a, a divided by x is greater than 1”, which is of course FALSE (because a positive number divided by a larger one will never be greater than 1 and there is no such number).

And now taking the definition of the limit of a sequence from the previous post:

We will read it like this (adding some explanations):

“For any greater than zero, we will find a term number of the sequence , such that for each term of the sequence with a number greater than the distance (absolute value is the distance) between this term of the sequence and the limit will be less than ”

We can also use more human language:

“No matter how small the distance is at the beginning, we will find a term number of the sequence, so that all subsequent terms of this sequence will be closer to the limit than the initially established distance “