Limits of Sequences with Logarithms

For the limits of many sequences with logarithms, you can confidently use the transformations and formulas for logarithms learned in high school. For example:

Example of a Limit of a Sequence with Logarithms


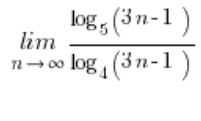
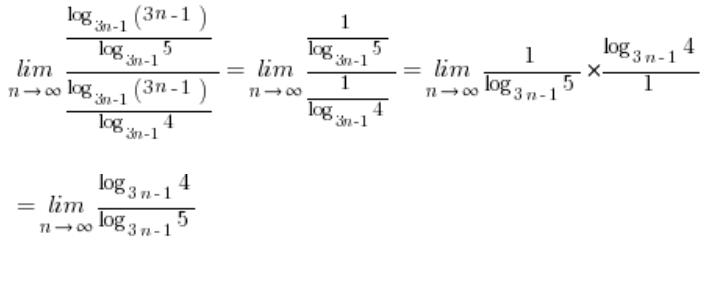
In situations where logarithms had different bases and there wasn’t much you could do about it, they were converted to a common base using the formula: 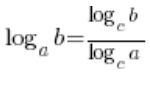. For our limit, it will be nice and convenient to take this base: . We then have the limit of the sequence:


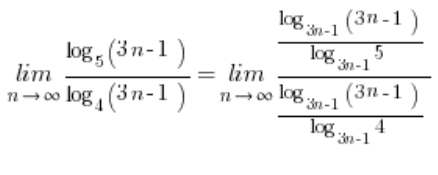
We know that , which in our expression is 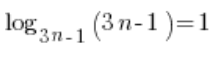. Therefore:


And this expression, using the high school formula again (but this time in reverse), will be equal to …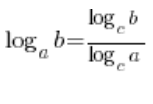


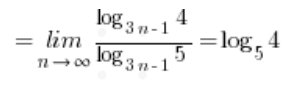
Which is of course the result (an irrational number).

There was no need to use any limit methods – just the high school logarithm transformations were enough.

Want to know more about calculating limits? I recommend my course 🙂

Krystian Karczyński

Założyciel i szef serwisu eTrapez.

Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.

Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.

Related Posts

Why can’t a function graph have two oblique asymptotes as x approaches positive infinity?

Posted on

Directional derivatives – something new again?

Posted on

Econometrics – What Is It Exactly?

Posted on

Leave a Reply

Your email address will not be published. Required fields are marked *

Your comment will be publicly visible on our website along with the above signature. You can change or delete your comment at any time. The administrator of personal data provided in this form is eTrapez Usługi Edukacyjne E-Learning Krystian Karczyński. The principles of data processing and your related rights are described in our Privace Policy (polish).