Definite integrals can be calculated with respect to variable x or y, and sometimes should be, if it’s more convenient. This often plays a big role in the applications of integrals, such as: calculating the area of regions, arc lengths, volumes, and surface areas of solids of revolution. Often we don’t even have a choice, because the conditions of the problem specify that the curve rotates around the OY axis, not the OX.
How do you do that?
First, you need to draw a diagram and mark the area/arc length/volume you need to calculate. Without this, we can’t get started.
Second, you need to determine the integration limits on the OY axis (similarly, as done on the OX axis).
Now, all you need to do is determine the bounding curves for the data (usually) with respect to variable x using variable y, for example, if we have the curve 
, we determine “x” and thus obtain two functions of variable y: 
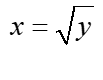and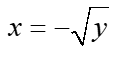 
.
Then we just create the appropriate integral with integration limits on the OY axis and functions of variable y, for example in the area of the region it would be:
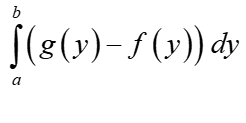
I’ll repeat again, the basis is a clear, large graph!
