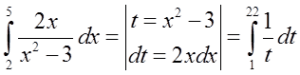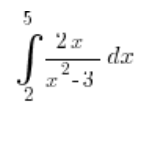
To tackle the above problem on definite integration, we need to use substitution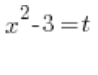 
, and we’re all on the same page here. But what about the limits of integration?
Integration Limits in Substitution Tasks for Definite Integrals
Can we write:
?
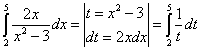Absolutely not. The issue with integration limits. In the definite integral on the left, they relate to variable
, and on the right to variable 
, so they must also change with the variable.
One approach (which I recommend in my course) is to completely sidestep the problem by solving the indefinite integral (without integration limits) on the side and then inserting the integration limits of 5 and 2 into the result (with variable x).
The other approach is to confront the problem head-on and change the integration limits according to the substitution. Since the limits in variable x are: 2 and 5, after substitution: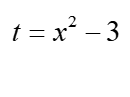 
they will be in variable t respectively: 1 and 22, and I obtained these results by substituting 2 and 5 for x in the substitution 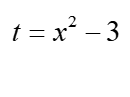. So the correct transition would be:
