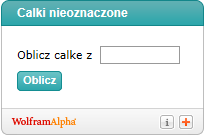
Calculator For Indeterminate Integrals (Check If You’re Counting Right).
Krystian Karczyński
27 April 2012
No Comments
Introducing the Wolfram calculator for indeterminate integrals, reworked a bit by me.
Two types of discontinuity (function limits)
Krystian Karczyński
18 January 2012
No Comments
As we all know (for example from my Limits Course), a function is continuous at the point x0 when the left-side limit of this function at this point is equal to the right-side limit of the function at this point and is equal to the value of the function at this point.
If any of the equality is not satisfied, the function f(x) is not continuous at the point x0, and the point is called a point of discontinuity. In this naming, you can go a step further and DISTINGUISH the points of discontinuity. See how to do it.
Calculator For Math Series
Krystian Karczyński
13 January 2012
No Comments
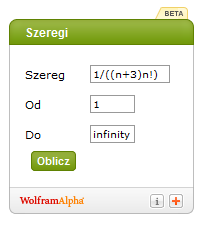
Introducing another Wolphram calculator, reworked slightly by me.
This toy below is for calculating the sum of series (not only numerical, but also functional!).
Euler Substitutions of the First Kind
Krystian Karczyński
5 January 2012
No Comments
Euler’s substitutions in indefinite integrals are the next thing introduced after rational integrals, trigonometric integrals, and root integrals. This means that most students won’t have the pleasure of encountering them, and I haven’t included them in my Course on Indefinite Integrals.
However, there remains quite a large group of students in mathematical fields who have to deal with Euler’s substitutions, and I invite these (and the curious) to join. I will discuss all three types of Euler’s substitutions (in this post I will cover the first type) and provide one example for each.
Some Things You Should Have Learned Well in High School But Nobody Told You So – Part 5 Multiplying or dividing inequalities on both sides
Krystian Karczyński
18 October 2011
No Comments
In this post, I will continue with topics from high school that you may not have placed much emphasis on, but which will make your life much easier when you go to college.
This is part 5 – if you just came here now, you can take a look at the previous 4 posts 🙂
Here I will deal with mutual multiplication and division of inequalities.
Wirtualny nauczyciel AI działający w przeglądarce internetowej.