Volume of a Solid of Revolution – Problem with a Catch
Krystian Karczyński
Founder and General Manager of eTrapez.
Graduate of Mathematics at Poznan University of Technology. Mathematics tutor with many years of experience. Creator of the first eTrapez Courses, which have gained immense popularity among students nationwide.
He lives in Szczecin, Poland. He enjoys walks in the woods, beaches and kayaking.
In the tougher problems on definite integrals, it’s always good to stay sharp – a task that seems super hard can be cracked with a simple formula from middle school.
Problem on the Volume of a Solid of Revolution
Let’s say we need to calculate the volume of a solid formed by rotating a curve:
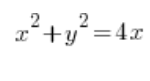
spinning (okay, let’s say “rotating”) around the OX axis. A few tidy moves known from high school…
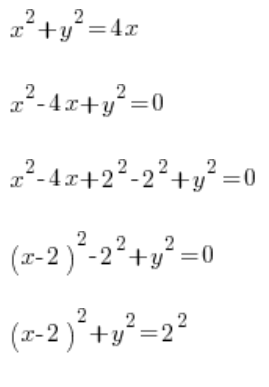
…and we realize that our curve is just a little circle with the center at point (2,0) and radius 2. What now? We derive y from the formula and push forward with the definite integral: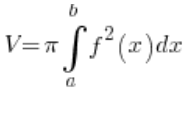 
?
Solution
No… Let’s pause for a moment. Take a deep breath. Think. A little circle… It rotates… What will result from such rotation? Obviously, a sphere. We know the formula for the volume of a sphere from middle school:
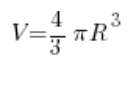
We already know the radius (it’s two), which means:
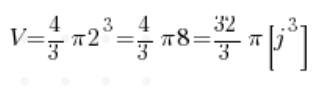
And there we have the answer, without even touching integrals 🙂
Are you looking for college or high school math tutoring? Or maybe you need a course that will prepare you for the final exam?
We are "eTrapez" team. We teach mathematics in a clear, simple and very precise way - we will reach even the most knowledge-resistant students.
We have created video courses translated in an easy, understandable language, which can be downloaded to your computer, tablet or phone. You turn on the video, watch and listen, just like during private lessons. At any time of the day or night.
