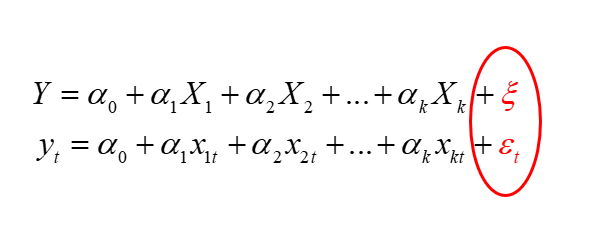Po co nam składnik losowy w modelu?

---

Ekonometria Wykład 3

Temat: Składnik losowy

 

Pod koniec poprzedniego Wykładu 2 wspomniałam jeden z powodów, dla których składnik losowy jest ważny w modelu ekonometrycznym. Dzięki jego obecności postać modelu nabiera charakteru stochastycznego, a nie deterministycznego.

Domyślam się, że to ostatnie zdanie nie jest do końca jasne. W tym Wykładzie wyjaśnię, o co chodzi.

 

Najpierw zajmijmy się samą definicją słów deterministyczny oraz stochastyczny. Według Słownika Języka Polskiego:

• Deterministyczny oznacza “uwarunkowany przyczynowo”, “nieprzypadkowy”; wszystkie zjawiska i działania są połączone związkiem przyczynowo-skutkowym, tj. są jednoznaczne.

W takim rozumieniu używając pojęcia deterministyczny masz po prostu masz do czynienia z czymś dokładnie określonym.

• Stochastyczny (z gr. stochasis – domysł) oznacza po polsku: “losowy”, “przypadkowy” .

Masz tu zatem do czynienia z czymś bardziej abstrakcyjnym, takim nie określonym dokładnie na 100%.

 

W zapisie matematycznym spotkać możesz takie oto modele:

MODELE DETERMINISTYCZNE – modele nie uwzględniające składnika losowego, czyli 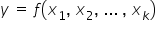 .  Jest to zwykła, konkretna funkcja, np. liniowa  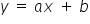. W innym zapisie, bardziej ekonometrycznym model ten wygląda następująco:  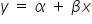 . Oznacza to, że każdej wartości zmiennej objaśniającej  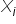 odpowiada konkretna wartość zmiennej .

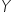MODELE STOCHASTYCZNE – modele uwzględniające składnik losowy, czyli 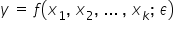 . W przypadku funkcji liniowej model wyglądałby następująco:  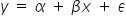.  Jednak nie przyporządkowuje się tutaj jednoznacznie wartościom  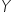wartości zmiennych  .

 

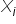Rodzi się pytanie – dlaczego więc większość modeli ekonometrycznych przyjmuje tę drugą postać? Weźmy pod uwagę kilka życiowych sytuacji.

 

Przykład 1

Pani Magda dostaje co miesiąc kieszonkowe. Jest to stała, regularna kwota, którą może wydać na dowolny dodatkowy zakup. Najczęściej kupuje jakiś super ciuszek po okazyjnej cenie. Jednak od czasu do czasu decyduje się na większy zapas kosmetyków, czy też na zakup innych potrzebnych jej drobiazgów.

Decyzja Pani Magdy co do zakupów jest uwarunkowana przede wszystkim cenami, dokładniej promocjami, jak i jej wolnym wyborem. 

 

Przykład 2

Przez najbliższy miesiąc postanawiasz zaplanować obiady dla Twojej rodziny (4 osoby). Stojąc przed wyborem menu, czy codziennie jedlibyście ten sam obiad? Uwzględniasz oczywiście ceny i możliwości.

Jedziesz na zakupy. Po dokonaniu wyboru, zadowolona wracasz do kasy, jednak po drodze natrafiasz na inne tańsze produkty. Stwierdzasz że teraz to bardziej Ci się opłaca. Zmieniasz wszystko, a z zaoszczędzonych pieniędzy bierzesz coś dodatkowego na deser, np. lody.

Wracasz zadowolona autem z zakupów i nagle samochód Ci się zepsuł. Dzięki pomocy sąsiada wracasz do domu, jednak późniejszą porą. Obiad zjecie według planu, jednak z deseru niestety już nic nie będzie. Lody się rozpuściły.

Zdarzenie losowe w postaci awarii samochodu wpłynęło na efekt końcowy (obiad). Nie było jednak tutaj Twojej woli.

 

Na podstawie powyższych przykładów można stwierdzić, że w działaniu podmiotów ekonomicznych dopuszczalne są przypadek oraz wolna wola. Oznacza to, że ten sam konsument w takich samych warunkach, postawiony wobec wyboru, może podjąć każdorazowo inną decyzję. Ponadto, nagłe losowe zdarzenie zmienia całkowicie jego wcześniejszy wybór.

 

Przykład 3

Teraz coś na większą miarę, w skali kraju. Omówmy efekty jeszcze jednego zdarzenia losowego, można powiedzieć kaprysu pogody, – zjawiska suszy w danym roku. Wiesz dobrze, że z ekonomicznego punktu widzenia ma to ogromne skutki w wielu dziedzinach gospodarki. Przede wszystkim poszkodowani są rolnicy. Ponoszą ogromne straty. Koszty związane z zasiewem, sadzeniem, pielęgnacją i innymi zabiegami nie są w stanie być pokryte przez plony. W konsekwencji spada produkcja zwierzęca na następny rok. Dochód gospodarstwa maleje. Niektórzy,  aby przetrwać do następnego roku zmuszani są zaciągnąć kredyty, a to z kolei hamuje rozwój gospodarstwa. W skali globalnej, fakt ten obniża też wartość produktu krajowego brutto (PKB). Rosną ceny na wybrane produkty spożywcze, co odbija się na zwykłych konsumentach. Niestety problem odczuwa też i prosta gospodyni, która musi przygotować obiad w zależności nie tylko od dostępności produktu, ale i od jego ceny.

Można by tak wymieniać i wymieniać.

 

Chciałam tutaj pokazać, że na wyniki modelowania ekonometrycznego znacząco wpływają też zmiany rożnych wielkości ekonomicznych. Zatem jeśli  byś chciał wykorzystać tu model ekonometryczny do prognozowania, z pewnością możesz napotkać pewne utrudnienia. Podstawą dokonania prognozy jest założenie, iż czynniki oddziałujące na zjawisko w przeszłości, będą w tym samym stopniu wpływać na to zjawisko w przyszłości.

Nawiązując do Przykładu 3, nagłe wystąpienie zjawiska suszy kolokwialnie mówiąc “psuje” tutaj to założenie. Wyniki prognozy przeprowadzonej na podstawie danych dla “dobrej pogody” będą całkowicie inne niż te otrzymane po tej klęsce.

Warto zauważyć, że wnioski przewidywane na podstawie modeli ekonometrycznych mają charakter przybliżony, a nie dokładny. A zatem, możesz tylko określić stopień prawdopodobieństwa ich realizacji.

 

Dlaczego uwzględniamy składnik losowy?

Składnik losowy obrazuje w danym modelu 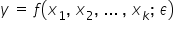 „zakłócenia” pomiędzy zmienną objaśnianą a zmiennymi objaśniającymi. Dlatego też przedstawia on sumaryczne oddziaływanie na zmienną objaśnianą wszystkich inne czynniki, m.in.:

• różnice między uproszczonym modelem a złożoną rzeczywistością;
• działanie czynników losowych i niespodziewanych zdarzeń (przypadkowości w działalności gospodarczej i życiu społecznym);
• niezgodna i niepoprawna postać funkcyjna modelu z faktycznymi zależnościami pomiędzy zmiennymi;
• wpływ innych zmiennych niż te, które są już w modelu (najczęściej drugorzędnych dla opisu badanego zjawiska);
• pominięcie ważnych zmiennych objaśniających;
• różnice wynikające z błędów obserwacji zmiennych i błędy obliczeń na nich wykonywanych;

 

Na koniec jeszcze wspomnę, iż “składnik losowy” to nie jedyne określenie na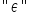(epsilon).  Możesz na swojej drodze spotkać jeszcze i inne wyrażenia: zaburzenie losowe, błąd losowy, składnik stochastyczny, zakłócenie, czy innowacja.

W zapisie modelu ekonometrycznego symbol 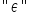(epsilon) może być też zapisywany inaczej, np.  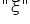(ksi),  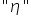(eta), itp.

 

Jak widzisz, dosyć sporo “siedzi” w tym składniku losowym. Dlatego jest to bardzo istotne, aby dopisywać go za każdym razem do ogólnej postaci modelu ekonometrycznego. Zwłaszcza, że jego własności będą odgrywały istotną rolę w weryfikacji modelu.