Jeśli zaczynasz przygody z ekonometrią i poznajesz budowę modeli ekonometrycznych, na pewno spotkałeś się na początku z najłatwiejszą do obliczeń i interpretacji postacią modelu – liniową:
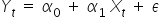 lub też w przypadku kilku zmiennych objaśniających:
lub też w przypadku kilku zmiennych objaśniających:
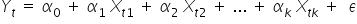
Jednak zależności między zmiennymi ekonomicznymi w rzeczywistości rzadko są ściśle liniowe. Mimo to ekonometria szczególnie często z nich korzysta. Choćby dlatego, że oprócz prostej interpretacji i obliczeń są postacią dla wielu modeli nieliniowych po ich linearyzacji.
To taka trochę przeróbka modeli nieliniowych na liniowe, za pomocą odpowiednich przekształceń matematycznych. Popatrz jak to można to zrobić w niektórych przypadkach 🙂
Nie wiem czy pamiętasz, ale w szkole średniej oprócz tej najprostszej funkcji 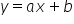 omawiane były także inne, nie wyrażone liniowo, ale np. poprzez postać wykładniczą, potęgową, kwadratową, wymierną, logarytmiczną itp. Sporo tego było, jedne były fajne, inne mniej ciekawe. Na ich podstawie można oczywiście również utworzyć modele. Będą one właśnie nieliniowe. A dokładniej – nieliniowe modele względem parametrów lub też nieliniowe modele względem zmiennych.
omawiane były także inne, nie wyrażone liniowo, ale np. poprzez postać wykładniczą, potęgową, kwadratową, wymierną, logarytmiczną itp. Sporo tego było, jedne były fajne, inne mniej ciekawe. Na ich podstawie można oczywiście również utworzyć modele. Będą one właśnie nieliniowe. A dokładniej – nieliniowe modele względem parametrów lub też nieliniowe modele względem zmiennych.
Konkretne przykłady? Proszę bardzo (dla pokazania wybrałam po dwie zmienne objaśniające):
model wykładniczy: 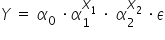 (czyli jest liczba (parametr) do potęgi zmiennej);
(czyli jest liczba (parametr) do potęgi zmiennej);
model potęgowy: 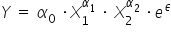 (tutaj z kolei jest zmienna do potęgi liczbowej);
(tutaj z kolei jest zmienna do potęgi liczbowej);
model logarytmiczny: 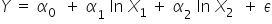 (na zmienne nałożone są logarytmy naturalne).
(na zmienne nałożone są logarytmy naturalne).
Zapytasz pewnie – jak wtedy oszacować parametry stojące przy zmiennych objaśniających? Jak je zinterpretować? Czy działa tutaj ta typowa Metoda Najmniejszych Kwadratów?
Nie do końca. Przynajmniej nie na tym etapie. Ale jest na szczęście i na to mały sposób 🙂 W tym artykule pokaże Ci jak przerobić (i zinterpretować!) takie modele przy użyciu działania logarytmowania.
Przykład 1
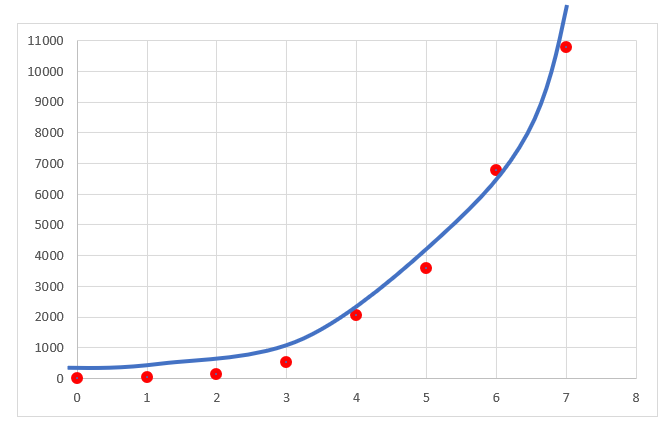
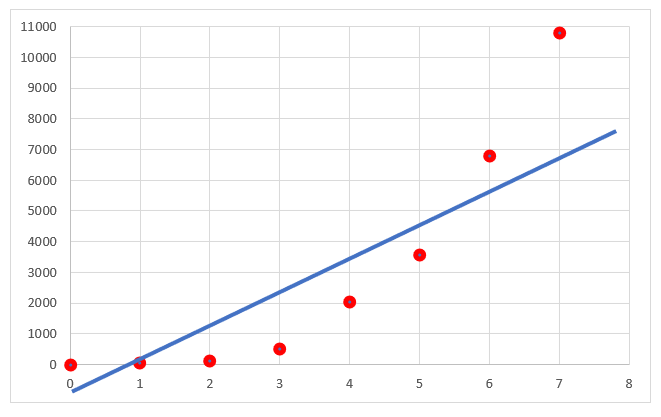
Poniższy rysunek ilustruje rozkład dwóch dowolnych zmiennych – objaśnianej Y oraz objaśniającej X.
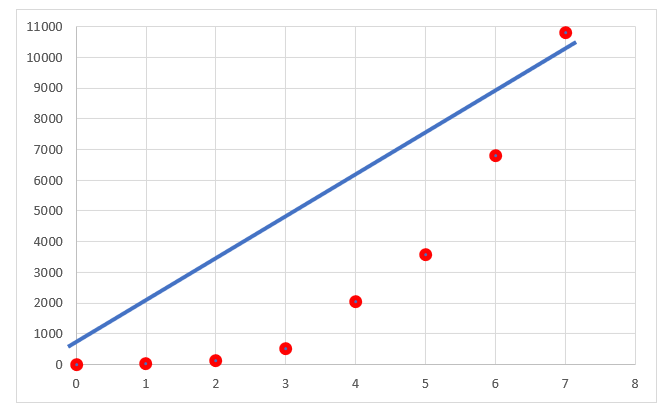
Co powiesz o tym zbiorze punktów? Czy da się je jakby „ogarnąć” jedną linią prostą?
Na przykład w taki sposób:
lub może tak lepiej ustawić linię?
Czy może ten zbiór punktów przypomina bardziej inny kształt?
Podobny jest nie do linii prostej, ale układa się w taką rosnącą falę, coś na wzór:
Jeśli przypomnimy sobie pewne wiadomości ze szkoły średniej, to taki typ wykresu miała właśnie FUNKCJA WYKŁADNICZA podawana podstawowym wzorem: 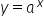 . Po uwzględnieniu przesunięć góra / dół wychodziło:
. Po uwzględnieniu przesunięć góra / dół wychodziło: 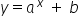 .
.
To był tylko przykładzik ilustrujący „wizualnie”, że zmienne mogą układać się nie tylko w sposób liniowy.
Poniżej pokaże Ci, jak na kilku wybranych modelach nieliniowych dokonuje się linearyzacji.
- Model POTĘGOWY
Postać ogólna modelu ekonometrycznego z jedną zmienną objaśniającą jest następująca:
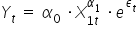
lub ogólny przypadek dla wielu zmiennych:

Sprowadzanie FUNKCJI POTĘGOWEJ do postaci LINIOWEJ WZGLĘDEM PARAMETRÓW:
Dla przykładu pokażę, jak dokonać linearyzacji modelu dla dwóch zmiennych objaśniających.
Na początku nałożę obustronnie na całe równanie logarytm naturalny
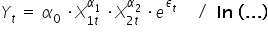
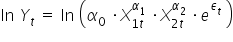
Z własności logarytmów wiemy, że 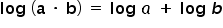 , stąd:
, stąd:
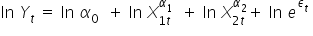
Wykorzystuję kolejną własność logarytmów, tzn: 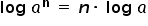 (potęga z liczby logarytmowanej leci do przodu przed logarytm).
(potęga z liczby logarytmowanej leci do przodu przed logarytm).
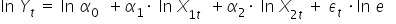
I jeszcze ostatnia drobnostka. Logarytm naturalny to to samo, co logarytm przy podstawie liczby „e”. Stąd zawsze otrzymasz, że: 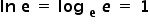 (bo logarytm z liczby o tej samej podstawie jakby „się skraca” i daje równiutko
(bo logarytm z liczby o tej samej podstawie jakby „się skraca” i daje równiutko 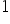 ).
).
Mamy więc ostatecznie zlinearyzowany model ekonometryczny, tzn. model liniowy względem parametrów.
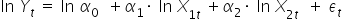
Jest on często określany jako model podwójnie logarytmiczny albo model logarytmiczno-liniowy.
Widzisz tutaj lekko przedefiniowane zmienne. Dla pokazania, że bezwarunkowo można uznać go za model liniowy, warto wprowadzić dodatkowe pomocnicze zmienne objaśniające, objaśnianą oraz pomocnicze parametry.
Uznam, że: 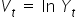 oraz
oraz 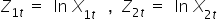 , a także, że
, a także, że 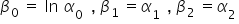 . Stąd:
. Stąd:
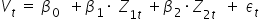
I tutaj możesz już śmiało szacować parametry przy pomocy klasycznej metody najmniejszych kwadratów, (którą z resztą dokładnie omówiłam w moim Kursie).
Przykład 2
Dla powyższego równania otrzymano (przykładowo oczywiście) następujące oszacowanie po zastosowaniu KMNK:
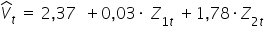
By „odtworzyć” oszacowaną postać potęgową modelu powracam do pierwotnych parametrów.
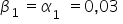 oraz
oraz 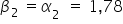 . Z wyrazem wolnym będą związane lekkie przekształcenia:
. Z wyrazem wolnym będą związane lekkie przekształcenia:
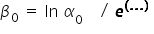
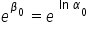
Wykorzystuję tutaj własność logarytmu naturalnego i liczby „e”, tzn. 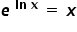 .
.
Czyli: 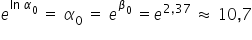
Mam więc ostatecznie oszacowany model 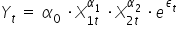 w postaci:
w postaci:
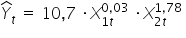
INTERPRETACJA:
Przykro mi, ale niestety nie pójdzie ona typowo jak dla modelu ściśle liniowego (popatrz np. mój wcześniejszy artykuł). No prawie nie pójdzie 🙂 Nie mamy tutaj samej zmiennej „Y” lub „X” , ale jest 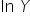 czy też
czy też 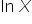 .
.
Jeżeli w równaniu regresji zmienną objaśnianą jest logarytm pewnej wielkości ekonomicznej (czyli np. 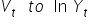 ), a zmienną objaśniającą jest logarytm naturalny jakiejś innej zmiennej (np.
), a zmienną objaśniającą jest logarytm naturalny jakiejś innej zmiennej (np. 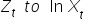 ), to ocenę parametru
), to ocenę parametru 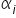 możesz interpretować stosując procenty w odniesieniu bezpośrednio do podanych wielkości.
możesz interpretować stosując procenty w odniesieniu bezpośrednio do podanych wielkości.
Czyli zamiast:
„… Jeśli 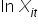 wzrośnie o
wzrośnie o 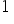 jednostkę… to wartość
jednostkę… to wartość 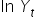 wzrośnie/spadnie o około
wzrośnie/spadnie o około 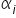 jednostek…. przy ceteris paribus.”
jednostek…. przy ceteris paribus.”
Powinieneś napisać:
„… Jeśli wartość
wzrośnie o
… to wartość
wzrośnie/spadnie o około
.. przy założeniu ceteris paribus”.
UWAGA: NIE mnożymy wartości parametru przez 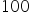 , ta liczba jest już wyrażona w % !
, ta liczba jest już wyrażona w % !
Jest to związane z tzw. elastycznością funkcji. Polecam o tym poczytać w innym Artykule 🙂
Jeszcze szybciutko wspomnę o interpretacji wyrazu wolnego 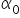 . Wyraża on poziom zmiennej zależnej Y, gdy wszystkie zmienne objaśniające przyjmują wartość
. Wyraża on poziom zmiennej zależnej Y, gdy wszystkie zmienne objaśniające przyjmują wartość 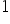 .
.
Wracając do Przykładu 2
Przypuśćmy, że 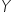 to wartość sprzedaży skarpetek [w mln zł],
to wartość sprzedaży skarpetek [w mln zł], 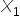 – dochód konsumenta [w zł], zaś
– dochód konsumenta [w zł], zaś 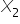 – wartość produkcji skarpetek w fabryce „Lanolina” [w mln zł].
– wartość produkcji skarpetek w fabryce „Lanolina” [w mln zł].
Interpretacja dla 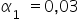 : „Jeśli wartość dochodu konsumenta wzrośnie o
: „Jeśli wartość dochodu konsumenta wzrośnie o 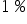 to wartość sprzedaży skarpetek wzrośnie o około
to wartość sprzedaży skarpetek wzrośnie o około 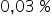 (a NIE
(a NIE 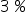 ), przy ceteris paribus (przy założeniu niezmiennej wartości produkcji)”.
), przy ceteris paribus (przy założeniu niezmiennej wartości produkcji)”.
Interpretacja dla 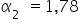 : „Jeśli wartość produkcji skarpetek w fabryce „Lanolina” wzrośnie o
: „Jeśli wartość produkcji skarpetek w fabryce „Lanolina” wzrośnie o 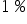 to wartość sprzedaży skarpetek wzrośnie o około
to wartość sprzedaży skarpetek wzrośnie o około 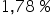 , przy ceteris paribus (przy założeniu niezmiennej wartości dochodu konsumenta)”.
, przy ceteris paribus (przy założeniu niezmiennej wartości dochodu konsumenta)”.
Widzisz? Nie jest jednak takie trudne 🙂
No to przechodzimy do drugiego typu modelu nieliniowego.
- Model WYKŁADNICZY
Postać ogólna modelu ekonometrycznego z jedną zmienną objaśniającą jest następująca:
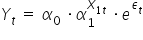
lub ogólny przypadek dla wielu zmiennych:
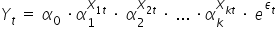
Sprowadzanie FUNKCJI WYKŁADNICZEJ do postaci LINIOWEJ WZGLĘDEM PARAMETRÓW:
Podobnie jak wcześniej, dokonam linearyzacji modelu dla dwóch zmiennych objaśniających.
Sytuacja jest identyczna. Zaczynam od zlogarytmowania równania
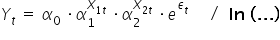
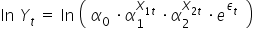
Z własności logarytmów 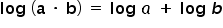 , czyli:
, czyli:
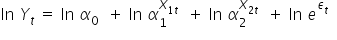
Dalej, wykorzystuję własność: 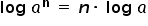
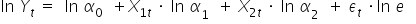
I ostatecznie, wykorzystując jak wcześniej to, że: 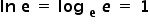 oraz porządkując wynik mamy:
oraz porządkując wynik mamy:
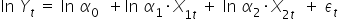
Jest on z kolei nazywany modelem połlogarytmicznym.
Zobacz, tym razem mamy troszkę inną sytuację niż wcześniej. Logarytm nałożony jest tylko na zmienną Y. Zmienne objaśniające są normalnie, są bez zmian brane do modelu. Parametry są z logarytmami, ale jak już wiesz, żadnym problemem to nie będzie 🙂
Podstawiam: 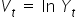 oraz
oraz 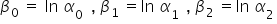 . Stąd:
. Stąd:
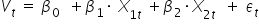
I tutaj znów możesz już śmiało szacować parametry przy użyciu KMNK.
Przykład 3
Powiedzmy, że dla powyższego równania otrzymano przykładowo takie oto oszacowanie parametrów strukturalnych:
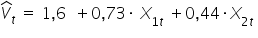
By „odtworzyć” oszacowaną postać potęgową modelu powracam do pierwotnych parametrów. Na wszystkie 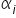 nałożony był logarytm, dlatego korzystam z przekształcenia (podobnie jak we wcześniejszym modelu):
nałożony był logarytm, dlatego korzystam z przekształcenia (podobnie jak we wcześniejszym modelu):
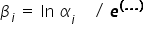
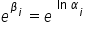 Stąd:
Stąd: 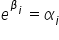
Czyli: 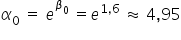 ,
, 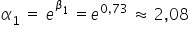 ,
, 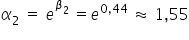 .
.
Mam więc ostatecznie oszacowany model 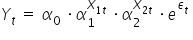 postaci:
postaci:
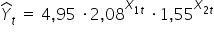
INTERPRETACJA:
Jeżeli w równaniu regresji zmienną objaśnianą jest logarytm pewnej wielkości ekonomicznej (czyli np. 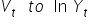 ), a zmienną objaśniającą jest wybrana zmienna (bez logarytmu, czyli po prostu
), a zmienną objaśniającą jest wybrana zmienna (bez logarytmu, czyli po prostu 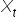 ), niestety, nie możesz powiedzieć:
), niestety, nie możesz powiedzieć:
„… Jeśli wartość 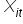 wzrośnie o
wzrośnie o 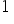 jednostkę… to wartość
jednostkę… to wartość 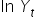 wzrośnie/spadnie o około
wzrośnie/spadnie o około 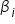 jednostek…. przy ceteris paribus.”
jednostek…. przy ceteris paribus.”
Taka interpretacja jest mało użyteczna – nie odnosi się bezpośrednio do wielkości ekonomicznych. Dziwnie brzmi, że np. logarytm sprzedaży (?), logarytm dochodu (?), itp. wzrośnie o daną wartość.
Aby przejść na bardziej przydatną interpretację, musisz sobie uświadomić, co oznacza „wzrost logarytmu o jednostkę”.
Jeżeli logarytm naturalny jakiejś zmiennej wzrośnie o „k” jednostek, jest to równoważne wzrostowi samej wielkości
razy (co zapisujemy też
).
Wzięło się to stąd, że: 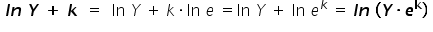 .
.
Czyli mamy ostatecznie taką interpretację dla tego typu modeli:
„… Jeśli wartość
wzrośnie o
jednostkę … to wartość
wzrośnie/spadnie około
razy.. przy założeniu ceteris paribus”.
Z racji tego, że doszliśmy już w naszych przekształceniach do wniosku, że: 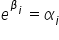 , mogę to również interpretować jako:
, mogę to również interpretować jako:
„… Jeśli wartość
wzrośnie o
jednostkę … to wartość
wzrośnie/spadnie około
razy.. przy założeniu ceteris paribus”.
Jeżeli potrzebujesz interpretacji w procentach, to musisz wziąć pod uwagę taki fakt związany z procentami. Wzrost np. 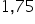 razy to wzrost o
razy to wzrost o 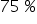 (czyli o
(czyli o 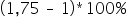 ). Ostatecznie więc możemy interpretować to tak:
). Ostatecznie więc możemy interpretować to tak:
„… Jeśli wartość
wzrośnie o
jednostkę … to wartość
wzrośnie/spadnie o około
.. przy założeniu ceteris paribus”.
Jeszcze napomknę jak interpretuje się wyraz wolny 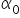 . Wyraża on poziom zmiennej zależnej Y, gdy wszystkie zmienne objaśniające przyjmują wartość
. Wyraża on poziom zmiennej zależnej Y, gdy wszystkie zmienne objaśniające przyjmują wartość 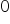 .
.
Wracając do Przykładu 3
Przypuśćmy, że zmienne mają takie same znaczenie jak w Przykładzie 2. Zmienna 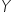 to wartość sprzedaży skarpetek [w mln zł],
to wartość sprzedaży skarpetek [w mln zł], 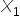 – dochód konsumenta [w zł], zaś
– dochód konsumenta [w zł], zaś 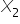 – wartość produkcji skarpetek w fabryce „Lanolina” [w mln zł].
– wartość produkcji skarpetek w fabryce „Lanolina” [w mln zł].
Interpretacja dla 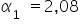 : „Jeśli wartość dochodu konsumenta wzrośnie o
: „Jeśli wartość dochodu konsumenta wzrośnie o 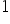 jednostkę, to wartość sprzedaży skarpetek wzrośnie około
jednostkę, to wartość sprzedaży skarpetek wzrośnie około 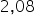 razy (lub
razy (lub 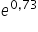 razy) , czyli wzrośnie o około
razy) , czyli wzrośnie o około 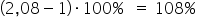 , przy ceteris paribus (przy założeniu niezmiennej wartości produkcji)”.
, przy ceteris paribus (przy założeniu niezmiennej wartości produkcji)”.
Interpretacja dla 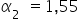 : „Jeśli wartość produkcji skarpetek w fabryce „Lanolina” wzrośnie o
: „Jeśli wartość produkcji skarpetek w fabryce „Lanolina” wzrośnie o 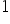 jednostkę, to wartość sprzedaży skarpetek wzrośnie około
jednostkę, to wartość sprzedaży skarpetek wzrośnie około 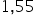 razy (lub
razy (lub 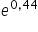 razy) , czyli wzrośnie o około
razy) , czyli wzrośnie o około 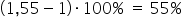 , przy ceteris paribus (przy założeniu niezmiennej wartości dochodu konsumenta)”.
, przy ceteris paribus (przy założeniu niezmiennej wartości dochodu konsumenta)”.
Zapytasz pewnie po co mi jest to potrzebne? Zwłaszcza takie dokładne (a czasami może i skomplikowane) interpretacje.
Żebyś umiał spoglądając na oszacowane równanie regresji wyrobić sobie zdanie, co te wyniki znaczą. Zawsze patrząc na uzyskane oceny parametrów staraj się wymyślić CO ONE ZNACZĄ i CZY SĄ SENSOWNE.
Poza tym, trzeba pamiętać o rozróżnieniu między zmienną w regresji a wielkością ekonomiczną i budować interpretacje tak, by były one ścisłe, prawdziwe, ale UŻYTECZNE i SENSOWNE – czyli jak najbliższe rzeczywistego problemu, wielkości które nas naprawdę interesują.
Wyklepanie formułki to żadna zasługa. Trzeba interpretować inteligentnie – wyobraź sobie, że piszesz raport dla niezbyt mądrego, ale strasznie upierdliwego szefa, którego nie obchodzą szczegóły obliczeń ani jak do wyniku doszedłeś, obchodzą go wyłącznie wnioski – ścisłe, prawdziwe ale podane tak, aby zrozumiał i aby do czegoś mu się to przydało.
Jeszcze jedna UWAGA. Przy interpretacjach pamiętaj (bo też często z tym się spotykałam na korepetycjach), by nie mówić „zmienna wzrośnie” , ale: „wartość zmiennej wzrośnie” (np. nie sprzedaż wzrośnie tylko wielkość sprzedaży wzrośnie). Wykładowcy są różni. Wiem, że niektórzy zwracają na to uwagę i chcą mieć interpretacje dopieszczone i w pełni poprawne 🙂
Powodzenia!
KONIEC


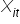 wzrośnie o
wzrośnie o 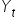 wzrośnie/spadnie o około
wzrośnie/spadnie o około 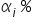 .. przy założeniu ceteris paribus”.
.. przy założeniu ceteris paribus”.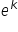 razy (co zapisujemy też
razy (co zapisujemy też 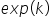 ).
).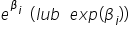 razy.. przy założeniu ceteris paribus”.
razy.. przy założeniu ceteris paribus”.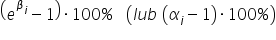 .. przy założeniu ceteris paribus”.
.. przy założeniu ceteris paribus”.
2 Comments
dfsdf
a co jeżeli wychodzi efekt \interakcji, dla dwóch zmiennych Y = X1 +X2 + X1*X2 + e ? Jak zinterpretować współczynniki?
Kamyk
A co z przypadkiem gdy nasze np. y = a+bx^c?