Skąd się bierze stała C w całkach nieoznaczonych? [REMASTERED]
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
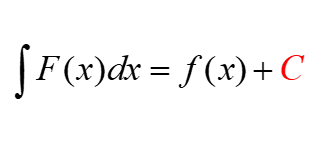
W rozwiązaniach całek nieoznaczonych na końcu dopisuje się tajemniczą stałą C. Co ona oznacza i skąd się bierze?
Ano bierze się ona właściwie z samej definicji całki nieoznaczonej. Całka nieoznaczona z funkcji 
to rodzina funkcji pierwotnych do tej funkcji. Funkcję nazywamy pierwotną do wtedy, kiedy jej pochodna równa jest .
Całka nieoznaczona to rodzina funkcji pierwotnych
Mówiąc inaczej całka nieoznaczona z jakiejś funkcji to zbiór wszystkich funkcji, których pochodna daje . Przyjrzyjmy się temu na przykładzie:
Całką nieoznaczoną z funkcji 
nazwiemy wszystkie funkcje, z których pochodna daje . Jakie mogą być to funkcje? Na przykład: 
. Ale nie tylko! Przecież pochodna z funkcji 
też daje . Analogicznie:
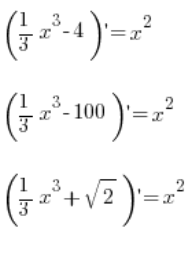
i ogólnie:
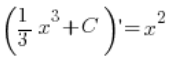– gdzie C oznacza dowolną stałą.
Stąd więc:
i stąd właśnie bierze się stała C w wyniku każdej całki nieoznaczonej.
Skoro całka nieoznaczona to cała rodzina funkcji, mamy więc też całą rodzinę wykresów.
Poniżej kilka takich rodzin (całek nieoznaczonych), różniących się o stałą C, którą możesz poustalać sobie dowolnie. Zobacz, jak różnić się mogą ich wykresy.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Mam takie pytanie egzaminacyjne. Jakie jest zastosowanie stalej calkowania C ? Nie jestem w stanie tego wymyslic. Prosze o pomoc.
Witam. Interpretacja np. fizyczna stałej C była by taka:
Pochodna oznacza prędkość.
Cała to funkcja liczona z prędkości, jej wynikiem jest funkcja drogi względem czasu.
Mając dany zapis “jak się zmieniała prędkość w czasie” możemy “zrekonstruować” jak się zmieniała droga w czasie. Nie możemy jednak dokładnie powiedzieć, gdzie był punkt początkowy tej drogi, gdzie ruch się rozpoczął.
Stała C (dowolna) to właśnie ten punkt początkowy drogi. Obierając np. C=10określamy, że przebyta droga rozpoczęła się dla wartości s=10km(jeżeli liczymy w kilometrach).
Polecam mój artykuł, gdzie wyjaśniam sprawy dokładniej:
https://blog.etrapez.pl/calki-nieoznaczone/calki-nieoznaczone-wprowadzenie/
Ja mam takie pytanie egzaminacyjne. Jakie jest zastosowanie stalej calkowania? Nie jestem w stanie tego wymyslic. Prosze o pomoc.
Po prostu zastosowałem elementarny wzór nr 16 z listy podstawowych wzorów na całki nieoznaczone:
Wzory na całki nieoznaczone
Jest on w Polsce używany o wiele częściej, niż ten z arcusem hiperbolicznym (który podpowiada np. Wolphram), o którym Pan pisze.
W tak prosty sposób wyjaśnione że dziecko z zerówki by to zrozumiało. Dzięki
Nie ma sprawy 🙂