Jak bardzo powiązane są zmienne, czyli o współczynniku korelacji liniowej Pearsona

Joanna Grochowska-Angielczyk

Kierownik Działu Nauczania eTrapez.
Absolwentka matematyki finansowej oraz informatyki i ekonometrii na Uniwersytecie w Białymstoku. Doświadczony korepetytor w zakresie przedmiotów matematycznych i ekonomicznych.
Mieszka w Białymstoku. Uwielbia podróżować i chodzić po górach. Wolny czas przeznacza na spotkania z rodziną i z przyjaciółmi. Lubi eksperymenty w kuchni oraz siatkówkę.

Ekonometria Wykład 5

Temat: Współczynnik korelacji liniowej Pearsona i jego istotność

Głównym celem ekonometrii jest zbadanie i zmierzenie pewnych powiązań zachodzących w zjawiskach ekonomicznych. Wyjaśnia ona po prostu zachowanie jednej zmiennej, w zależności od zachowania innych zmiennych. Logiczne więc jest, by wybrane do modelu zmienne objaśniające 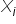  były jak najbardziej powiązane z objaśnianą 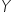.  Nie będziesz przecież tłumaczył np. wartości rocznych wydatków na paliwo od ilości lotów na księżyc. 🙂

Przejdźmy zatem do tematu, jak “fachowo” nazwać ten związek oraz jak zmierzyć siłę tego powiązania.

Zależność statystyczna, inaczej KORELACJA, oznacza związek pomiędzy dwiema zmiennymi losowymi. Analiza korelacji służy do “wychwycenia” czy w ogóle taki związek zachodzi oraz mierzy jego siłę.

Co oznacza związek? Istnieje oczywiście podobieństwo, przynajmniej przez analogię, do związków międzyludzkich.  Należy jednak go rozumieć jako rodzaj podobieństwa w “zachowywaniu się dwóch cech”. Gdy jedna cecha wzrasta to czy druga również wzrasta? A może maleje? A może w ogóle się nie zmienia? Na przykład, czy zachodzi związek pomiędzy notowaniami ropy naftowej a akcjami wybranej spółki paliwowej?

Intuicyjnie, zależność dwóch zmiennych oznacza, że znając wartość jednej z nich, dałoby się częściej dokładniej przewidzieć wartość drugiej zmiennej, niż bez tej informacji.

Najbardziej popularną odmianą korelacji jest korelacja liniowa. Dotyczy ona zależności liniowej, tzn. jeżeli coś rośnie to drugie jednocześnie też rośnie lub spada. Miej jednak na uwadze, że można obliczać również zależności kwadratowe, sześcienne itd.

Najważniejszym miernikiem siły związku prostoliniowego dwóch cech jest współczynnik korelacji liniowej Pearsona. Liczy się go pomiędzy zmiennymi mierzalnymi.

Współczynnik korelacji liniowej Pearsona

Ogólny wzór na obliczenie wartości współczynnika korelacji Pearsona dla dwóch zmiennych X i Y.

Wykorzystać tutaj musisz kowariancję między zmiennymi dzieloną przez iloczyn ich odchyleń standardowych. Wszystkie obliczenia krok po kroku, również jak się ten współczynnik interpretuje, pokazałam dokładnie w Lekcji 2 (cz. 1) mojego Kursu. Przedstawiłam tam nie tylko “ręczne” rachunki, ale również jak możesz szybciutko to zrobić za pomocą Excela.

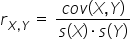
Standardowo wynik analizy korelacji – współczynnik korelacji dostarcza nam trzech informacji:

Gdyby odnotowano istotny, ujemny współczynnik korelacji pomiędzy wagą a wzrostem u ludzi to można byłoby stwierdzić, że wyższym osobom towarzyszy mniejsza waga (wyżsi ludzie mniej ważą).

Graficzną interpretacją współczynnika korelacji jest tzw. wykres rozrzutu

Przykłady wykresików dla dwóch cech X i Y:

lub też:

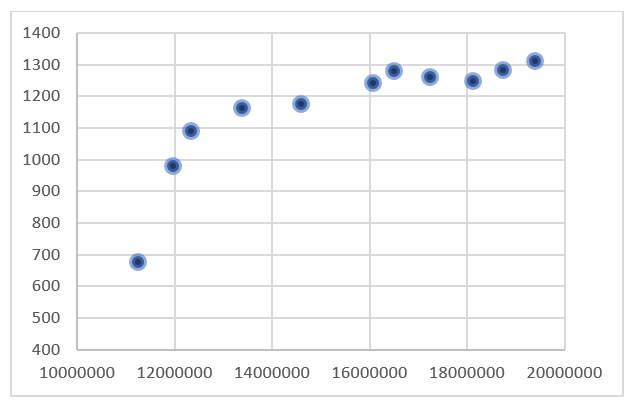
Poniżej popatrz na kilka przykładów jak układa się “chmura” punktów w zależności od wartości współczynnika korelacji liniowej Pearsona.

Źródło: https://pl.wikipedia.org/wiki/Zależność_zmiennych_losowych

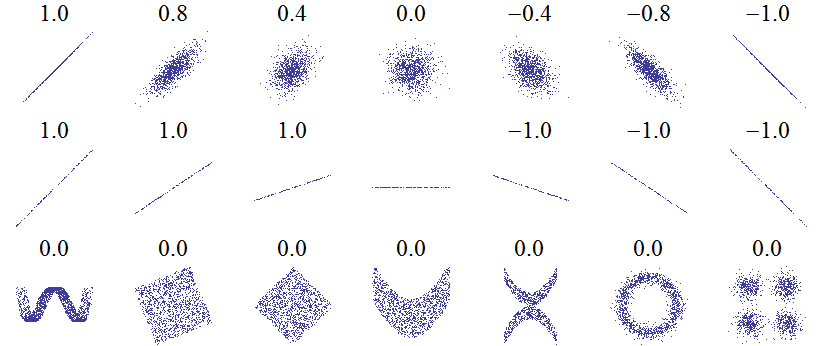
Należy również zwrócić uwagę na pewne pułapki tego współczynnika i jego mankamenty. Może on czasami dawać nie do końca wiarygodne wartości. Dzieje się tak w przypadku, gdy nie mamy do czynienia z rozkładem normalnym zmiennej (bo taki jest najbardziej preferowany). Innym powodem zaburzającym wynik korelacji są tzw. przypadki odstające.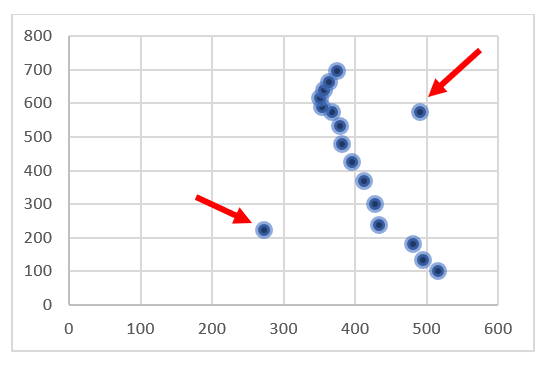

Punkty te nie do końca pasują do całej reszty. Można tu zaobserwować silną ujemną zależność, aczkolwiek wartość współczynnika korelacji może być zaburzona przez jeden czy dwa warianty odstające, które zniekształcają wynik.

Dlatego zanim przejdziesz do obliczeń, wykonaj na początku wykres rozrzutu dla dwóch zmiennych. Jeśli zauważysz na wykresie jakieś kropki ewidentnie odtrącające od całej reszty, wyeliminuj daną obserwację ze zbioru. Jest to jednak praktyka dosyć ryzykowna, niekiedy uważana za niedozwoloną.

Gdy wykonasz wykresu i obliczysz wartości współczynnika korelacji, zbadaj jeszcze jego istotność.

Testowanie istotności współczynnika korelacji

Ostatnim zagadnieniem, które omówię w tym Wykładzie jest odpowiedź na pytanie o istotność współczynnika korelacji liniowej Pearsona. Czy w populacji generalnej zachodzi podobny związek do zaobserwowanego w populacji próby? Czy też jest on jedynie dziełem przypadku? Aby to zbadać musimy założyć, że w najgorszym razie obie badane cechy mają rozkłady zbliżone do normalnych (warunek stosowalności poniższego testu). W przypadku znacznych odchyłek od tego założenia istnieje konieczność zastosowania testów nieparametrycznych.

Test do sprawdzania istotności współczynnika korelacji liniowej Pearsona służy do weryfikacji hipotezy o braku zależności liniowej pomiędzy badanymi cechami populacji. Opiera się na współczynniku korelacji liniowej Pearsona wyliczonym dla próby. Im wartość współczynnika  r  jest bliższa zeru, tym słabszą zależnością związane są badane cechy.

Statystyka testowa wymaga hipotezy zerowej 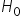 w brzmieniu: prawdziwa wartość współczynnika korelacji (ta z populacji generalnej, oznaczana jako “ro” 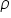) jest równa 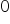. Jest to jest równoważne brakowi korelacji. Hipoteza alternatywna uznaje występowanie korelacji między zmiennymi. Oznacza to, że współczynnik jest różny od zera.

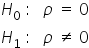
Do weryfikacji tej hipotezy służy statystyka:

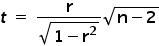
gdzie:
r – jest wyliczoną z próby wartością współczynnika korelacji Pearsona,
n – liczebnością próby.

W warunkach słuszności hipotezy zerowej statystyka t ma rozkład t – Studenta z df = n-2 stopniami swobody.

Z tablic rozkładu t- Studenta (dołączonych oczywiście do Kursu), lub kalkulatora, odczytujemy dla wcześniej przyjętego poziomu istotności 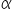 – wartość krytyczną  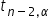. Poziom istotności to taki margines błędu. Przyjmuje bardzo małe wartości, najczęściej 0,05 czy też 0,01.

Jeżeli obliczona wartość t znajduje w dwustronnym obszarze krytycznym 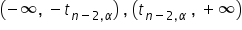, to 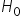 należy odrzucić na korzyść hipotezy alternatywnej.

Dokładniej, gdy:
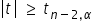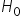 –  odrzucamy. Wartość współczynnika korelacji istotnie różni się od zera. Zatem zmienne te są skorelowane ze sobą.
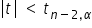 – nie ma podstaw do odrzucenia 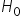. Otrzymana z próby różna wartość współczynnika korelacji wynikła z przypadku.

Przykład 4

Sprawdzimy dla przykładu, czy współczynnik korelacji między zmienną Y  a X, równy 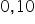, jest istotnie rożny od zera.

Stawiamy hipotezę zerową 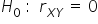 , wobec hipotezy alternatywnej .

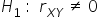Wyznaczam sprawdzian hipotezy zerowej, wiedząc, że liczba obserwacji w próbie :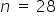

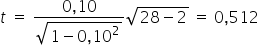
Dla poziomu istotności 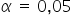 oraz dla  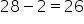stopni swobody odczytuję z tablic rozkładu t-Studenta wartość krytyczną .

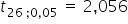Ponieważ 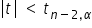 , zatem nie ma podstaw do odrzucenia hipotezy zerowej, że zmienne Y  oraz X nie są istotnie skorelowane.

Na podstawie korelacji skonstruowano wiele bardziej zaawansowanych technik analitycznych, co sprawia, że jest ona jedną z najbardziej popularnych i obecnych miar statystycznych.

Współczynnik ten przewija się przez ekonometrię w kilku miejscach. Przede wszystkim w metodach dobru zmiennych do modelu. Niemal w każdej metodzie. Czasami się zdarza, że mimo wysokiej wartości współczynnika korelacji może się okazać, że jest on nieistotny. Zatem powiązanie między wybranymi zmiennymi X i Y  nie jest prawdziwe. Stąd już na początku, zanim wybierzesz konkretną metodę doboru zmiennych, możesz dokonać eliminacji i ukrócić sobie dalszych obliczeń.

KONIEC

Kliknij, aby powtórzyć sobie, skąd pobrać i jak można zaprezentować zebrane dane (poprzedni Wykład) <–

Kliknij, aby sprawdzić, czym jest regresja i jak działa metoda najmniejszych kwadratów (następny Wykład) ->

Kliknij, aby powrócić na stronę z Wykładami do ekonometrii