Polynomgleichungen vierten Grades in komplexen Zahlen
Krystian Karczyński
Gründer und Chef des Dienstes eTrapez.
Master of Mathematics der Technischen Universität Pozen (Polen). Mathematik-Nachhilfelehrer mit langjähriger Erfahrung. Schöpfer der ersten eTrapez-Kurse, die bei Studenten in ganz Polen große Beliebtheit erlangten.
Lebt in Stettin (Polen). Mag Waldspaziergänge, Strandtage und Kajakfahren.
Beim Lösen von Aufgaben mit komplexen Polynomgleichungen verwenden wir im Allgemeinen dieselben Methoden wie beim Lösen von reellen Polynomgleichungen in der Oberstufe.
Viertgradige komplexe Gleichungen, die auf zweiten Grad reduzierbar sind
Das gilt auch für viertgradige komplexe Gleichungen, die auf zweitgradige Gleichungen reduziert werden können, also solche, bei denen wir eine Variable zur vierten Potenz, zur zweiten Potenz und einen konstanten Term haben, zum Beispiel:
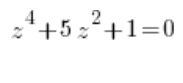
oder:
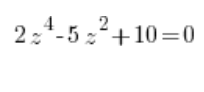
Wir reduzieren diese Art von komplexen Gleichungen auf komplexe Gleichungen zweiten Grades durch das Einsetzen von 
, wobei 
natürlich die komplexe Variable ist.
Aufgabe
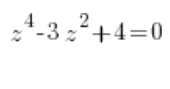
Wir setzen (natürlich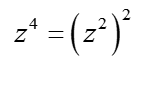 
) ein, so erhalten wir:
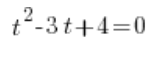
Und so lösen wir diese Gleichung auf die übliche Weise mit der Diskriminante (natürlich existieren Wurzeln negativer Zahlen in den komplexen Zahlen). Wir erhalten zwei komplexe Lösungen:
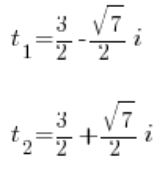
Da wir ersetzt haben: , haben wir:
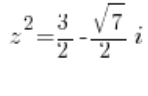
oder:
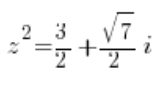
Das heißt:
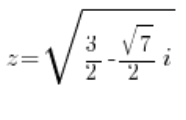
oder:
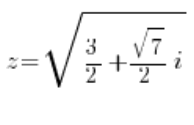
Nach der Berechnung der Wurzeln (natürlich werden es vier komplexe Wurzeln sein), werden wir vier Lösungen haben:
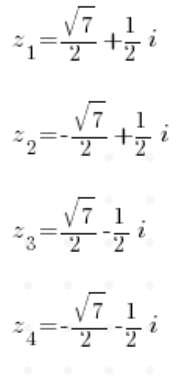
P.S. Ich zeige diese und andere Methoden in Lektion 6 meines Kurses zu komplexen Zahlen, schaut vorbei!
Suchen Sie nach Mathe-Nachhilfe für das Universitätsniveau oder die Oberstufe? Oder benötigen Sie vielleicht einen Kurs, der Sie auf das Abitur vorbereitet?
Wir sind das Team von eTrapez. Wir unterrichten Mathematik auf eine klare, einfache und sehr detaillierte Weise - wir erreichen sogar diejenigen, die sich am meisten gegen das Lernen sträuben.
Wir haben Kurse in Videoform erstellt, die in einer verständlichen Sprache erklärt sind, zum Herunterladen auf Computer, Tablet oder Handy. Sie starten die Aufnahme, schauen und hören zu, als wären Sie bei der Nachhilfe. Zu jeder Tages- und Nachtzeit.
