Reduzieren von einigen vierten Grades Gleichungen auf quadratische Gleichungen
Viele polynomiale Gleichungen vierten Grades können mit einem bekannten Highschool-Trick, der hier beschrieben wird, in quadratische Gleichungen umgewandelt werden:
Reduzieren auf eine quadratische Gleichung
Dies funktioniert natürlich auch für Polynome in komplexen Zahlen.
Zur Erinnerung, was wir tun haben wir die Gleichung:
{{z}^{4}}+3{{z}^{2}}+2=0Wir setzen: {{z}^{2}}=t
Und wir erhalten eine quadratische Gleichung:
{{t}^{2}}+3{t}+2=0Dann lösen wir sie mit dem üblichen Delta und so weiter, wir erhalten Lösungen 
, wobei wir daran denken, dass 
wir daraus zwei neue Gleichungen bilden:
oder 
Wir lösen sie und haben vier Lösungen: 
.
Reduzieren von einigen höheren Grades Gleichungen auf quadratische Gleichungen
Es gibt absolut nichts, was dagegen spricht, diese Methode auf Gleichungen höheren Grades als 4 auszudehnen (wenn sie natürlich durch Substitution auf quadratische reduziert werden können).
Also haben wir:
2{{z}^{6}}-5{{z}^{3}}+4=0Man kann auch feststellen, dass es gleichwertig ist:
2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0Und nach dem Einsetzen: 
Erhalten wir eine quadratische Gleichung:
2{{t}^{2}}-5t+4=0In der Gleichung:
{{x}^{10}}-3{{x}^{5}}+1=0Nach dem Einsetzen: 
Haben wir:
{{t}^{2}}-3t+1=0Und so weiter, und so weiter…
Beispiel
Nehmen wir die Gleichung:
z^6+(1-i)z^3-i=0Wir setzen z^2=t und haben:
t^2+(1-i)t-i=0Dann rechnen wir:
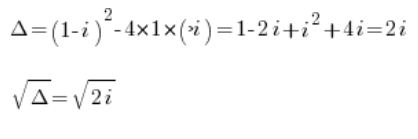
Wir berechnen diese Wurzeln mit den Methoden, die aus komplexen Zahlen bekannt sind (zum Beispiel in meinem Kurs gezeigt).
Wir haben 
oder 
Das heißt:
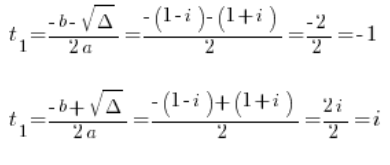
Denken Sie daran, dass dies noch keine Lösungen sind, da z^3=t
Also haben wir die Gleichungen zu lösen:
z^3=-1Und:
z^3=iWir transformieren sie zu:
und 
Und wieder mit den bekannten Methoden berechnet, haben wir drei Wurzeln aus der ersten Gleichung:
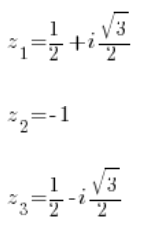
Und drei Wurzeln aus der zweiten Gleichung:
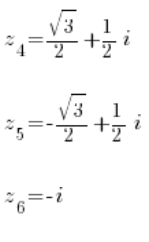
Gelöst 🙂
