Nehmen wir das folgende Folgenlimit:
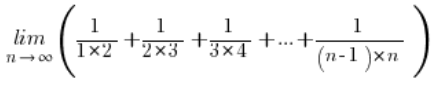
Bei der Aufgabe „fühlen” wir irgendwie, dass wir die Summenformeln für Folgen (arithmetisch oder geometrisch) verwenden müssen, aber leider, leider… Diese Folge ist weder arithmetisch noch geometrisch…
Was tun?
Wir müssen es völlig anders machen. Jeder Bruch wird in einfache Brüche zerlegt. Das wird ziemlich intensiv gemacht, wenn man sich mit unbestimmten Integralen von rationalen Funktionen beschäftigt, zum Beispiel. Die Idee ist, Konstanten A und B zu finden, sodass…
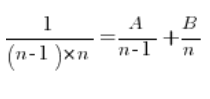
Wir multiplizieren beide Seiten der obigen Gleichung mit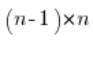 
und erhalten:
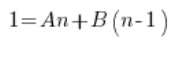
Weiter:
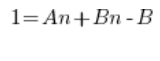
Wir vergleichen die Koeffizienten der Polynome auf der linken und rechten Seite (Polynomgleichheit – Gymnasium) und erhalten ein Gleichungssystem:
Aus der zweiten Gleichung: 
.
Das in die erste Gleichung eingesetzt:
Wir erhalten auch 
.
Unser beliebiger Bruch kann also zerlegt werden in:
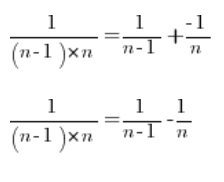
Kehren wir also zu unserem Folgenlimit zurück und zerlegen jeden Bruch in einfache Brüche:
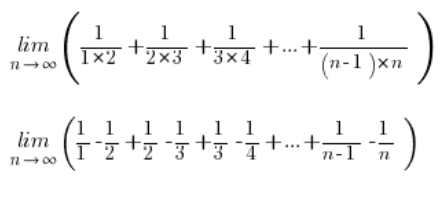
Wenn wir einige Terme kürzen, bleibt uns:
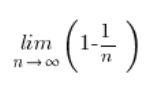
Und dieses Folgenlimit ist natürlich nicht mehr erschreckend:
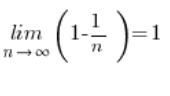
P.S.
Viele interessante Beispiele für Folgenlimits findest du in meinem Videokurs zu Limits.
