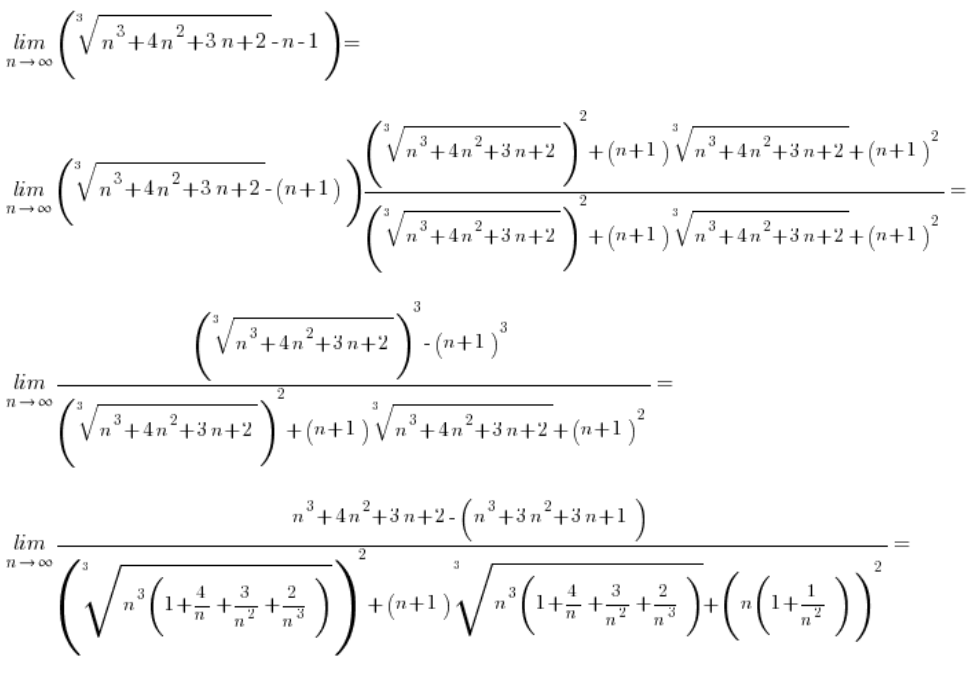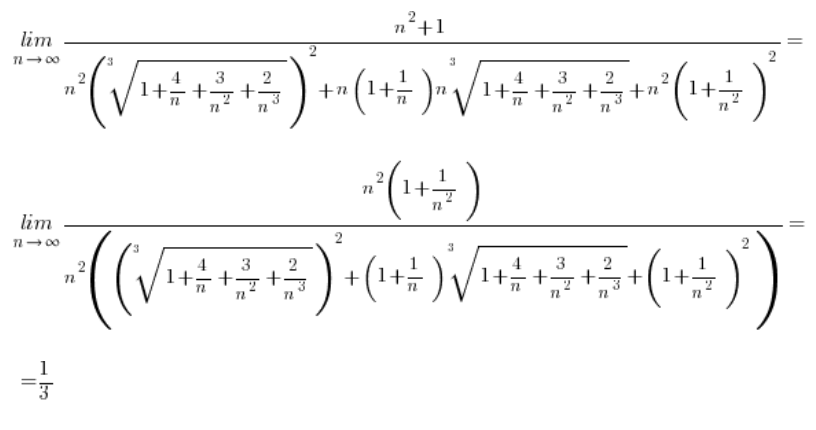Es befinden sich momentan keine Produkte im Warenkorb.
Krystian Karczyński- 5 August 2024
- Komentarz 0
Wie sah es mit „normalen“ Wurzeln aus?
Wenn wir einen zu berechnenden Grenzwert hatten, der irgendwie eine Subtraktion mit einer Wurzel beinhaltete (und den man natürlich nicht einfacher berechnen konnte), also:
„Etwas – Quadratwurzel von etwas“
„Quadratwurzel von etwas – Etwas“
„Quadratwurzel von etwas – Quadratwurzel von etwas“
wendeten wir einen Trick an, den ich „Multiplikation mit dem Konjugierten“ nenne.
Wir multiplizierten diesen Ausdruck einfach mit seinem Gegenstück mit einem Pluszeichen, oder vielmehr mit einem Bruch, bei dem dieses Gegenstück im Zähler und im Nenner war.
Zum Beispiel:
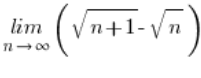wir multiplizierten so: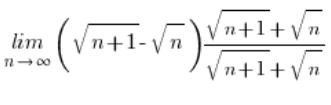 
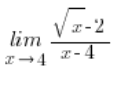wir multiplizierten so: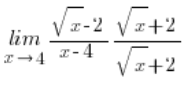 
Dieser clevere Trick ermöglichte es uns, die Formel der verkürzten Multiplikation zu erreichen:
Nachdem wir diese Formel erreicht hatten, „kürzten“ die Quadrate die Wurzeln und wir kamen auf eine einfache Lösung (naja, sagen wir manchmal eine etwas längere einfache Lösung).
Aber was ist mit der Situation, wenn die Wurzeln in der Subtraktion Kubikwurzeln sind? Wie hier zum Beispiel:
\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}Die Standardmethode, also das Multiplizieren auf folgende Weise:
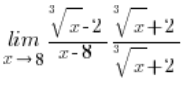
Hilft uns nicht, weil dieses Mal im Zähler nach dem Erreichen der Formel:
Die Quadrate die Kubikwurzeln in keiner Weise „kürzen“ werden. Also bleiben wir weiterhin stecken.
Wie wird es mit Kubikwurzeln aussehen?
Im Falle einer Subtraktion mit Kubikwurzeln müssen wir einfach auf ein völlig anderes Muster „zielen“ (aber auch aus der Mittelstufe), nämlich:
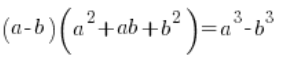
Also unsere gegebenen 
(bei denen a oder b oder beide Kubikwurzeln sind) werden wir statt mit 
mit 
multiplizieren und nach Anwendung der Formel werden die Kuben ihre Arbeit machen und die Wurzeln „kürzen“.
Beispiel 1
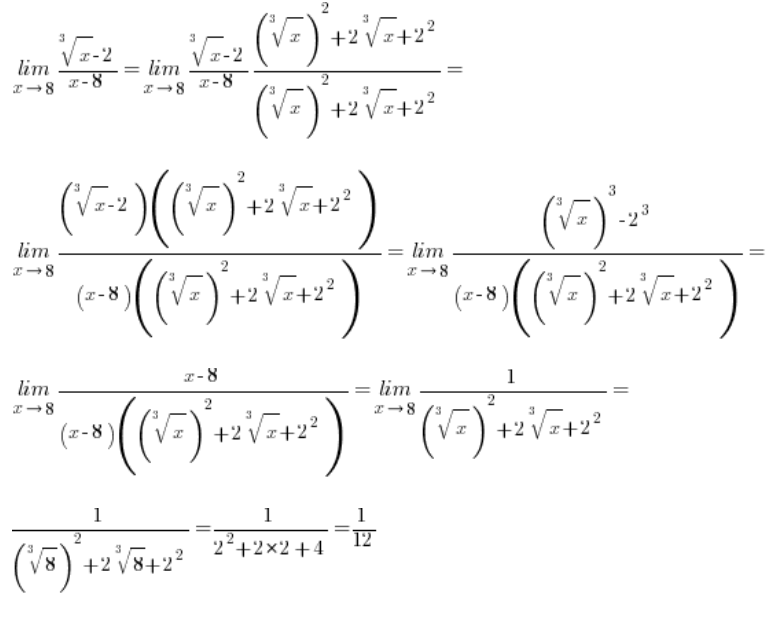
Beispiel 2
