Euler-Substitutionen der dritten Art – Zusammenfassung

---

Euler-Substitutionen der ersten, zweiten und dritten Art – Mehr braucht man nicht

In den vorherigen Beiträgen habe ich gezeigt, wie man Euler-Substitutionen in Integralen vom Typ:

• Euler-Substitutionen der ersten Art (wenn a>0)
• Euler-Substitutionen der zweiten Art (wenn c>0)

In diesem Beitrag beschäftigen wir uns mit der dritten und letzten Art der Euler-Substitutionen, die wir anwenden können, wenn im Integral:

das quadratische Polynom , zwei verschiedene Wurzeln hat , also wenn sein , also wenn es in faktorisierter Form geschrieben werden kann: .

Bevor wir jedoch zur Sache kommen, sollten wir beachten, dass diese drei Fälle:

• Erste Art, wenn a>0
• Zweite Art, wenn c>0
• Dritte Art, wenn es zwei verschiedene Wurzeln gibt

uns erlauben, jedes Integral vom Typ zu lösen:

Tatsächlich reichen sogar nur die erste und die dritte Art aus.

Warum?

Den Fall, wenn können wir ignorieren, weil das quadratische Polynom einfach in die lineare Form übergeht, die wir mit einfacheren Substitutionen als denen von Euler lösen können.

Was aber, wenn a<0 (passt nicht zur ersten Art) und das quadratische Polynom eine oder keine Wurzeln hat (passt nicht zur dritten Art)?

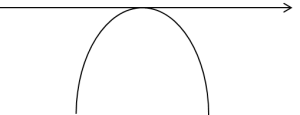
Dann würde sein Graph so aussehen (erinnert euch an die Schule – Arme nach unten):

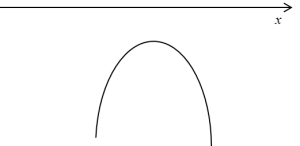
oder, wenn es überhaupt keine Wurzeln hätte, so:

Was ist die Schlussfolgerung? Dass in beiden Fällen das quadratische Polynom negative Werte annehmen würde (außer höchstens einem Punkt), und ich erinnere euch daran, dass wir das Integral berechnen:

Das bedeutet, dass das quadratische Polynom in der Funktion unter der Wurzel steht, und die Wurzel kann nicht aus negativen Werten berechnet werden (wir spielen natürlich mit reellen Zahlen). Das bedeutet, dass der Definitionsbereich einer solchen Funktion höchstens ein Punkt wäre, was also keinen Sinn ergibt, und ein solches Beispiel werden wir sicherlich nicht bekommen. Es sei denn, der Professor ist beim Erstellen der Beispiele für die Klausur wirklich unausgeschlafen.

Der Fall, wenn a<0 und das quadratische Polynom keine zwei Wurzeln hat, kann also ignoriert werden, und jetzt ist deutlich zu sehen, dass die erste und dritte Art der Euler-Substitutionen zu jedem Integral vom Typ passt:

Also, los geht’s mit der dritten Art der Euler-Substitutionen.

Euler-Substitutionen der dritten Art

Wir haben ein Integral:

,

in dem hat , also kann es geschrieben werden als:

,

wo sind seine Wurzeln.

Die Substitution, die wir hier verwenden, ist:

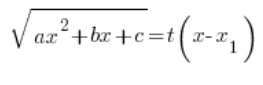
Wir quadrieren diese Substitution, schreiben das quadratische Polynom auf der linken Seite in faktorisierter Form (wir wissen, dass wir das können), teilen beide Seiten durch , und fahren wie bei den vorherigen Substitutionen fort, indem wir der Reihe nach bestimmen:

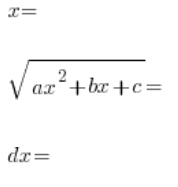
Schließlich setzen wir alles in das ursprüngliche Integral ein und kommen zu einem in der Regel mühsamen rationalen Integral.

Lasst uns anfangen.

Beispiel

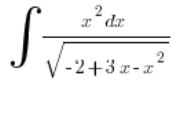
Unser (das heißt, a<0, also verwenden wir nicht die Substitutionen der ersten Art), unser (das heißt, c<0, also verwenden wir nicht die Substitutionen der zweiten Art), aber unser , das heißt, wir können die Substitutionen der dritten Art verwenden.

Zuerst berechnen wir :

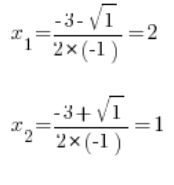
Wir verwenden die Euler-Substitution der dritten Art:

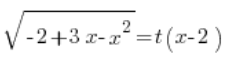
Wir quadrieren beide Seiten:

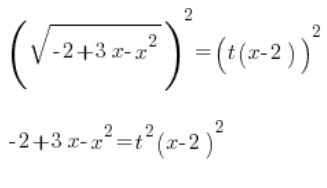
Wir schreiben das quadratische Polynom auf der linken Seite in faktorisierter Form (denken Sie daran hier!!!):

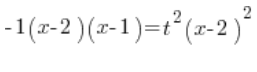
Wir teilen beide Seiten durch :

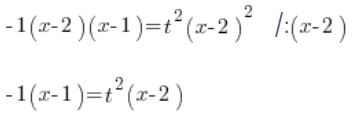
Wir bestimmen :

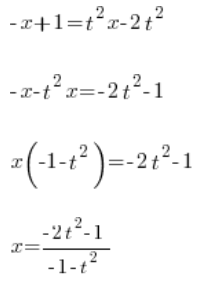
Wir haben mit Hilfe der Variable bestimmt. Jetzt bestimmen wir .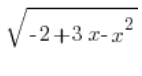

Zurück zu unserer ersten Substitution haben wir:

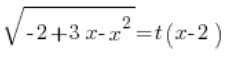
Wir setzen das bestimmte 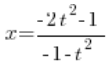ein, und wir haben:

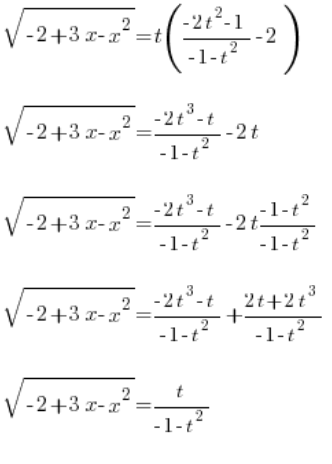
Wir haben 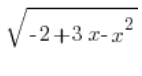schön bestimmt. Jetzt bleibt nur noch , das wir durch Berechnung der Ableitung von berechnen:

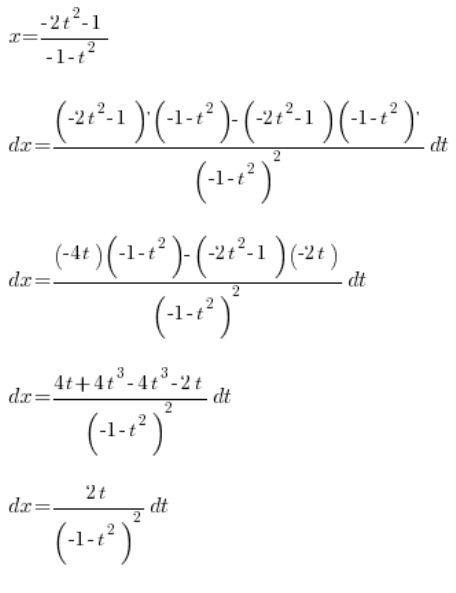
So haben wir bestimmt:

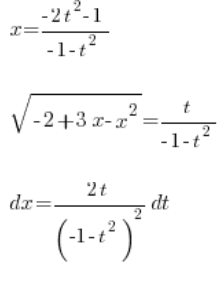
, alles mit Hilfe der Variable . Wir setzen das in das Integral ein:

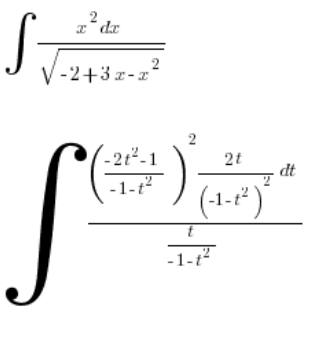
Wir vereinfachen:

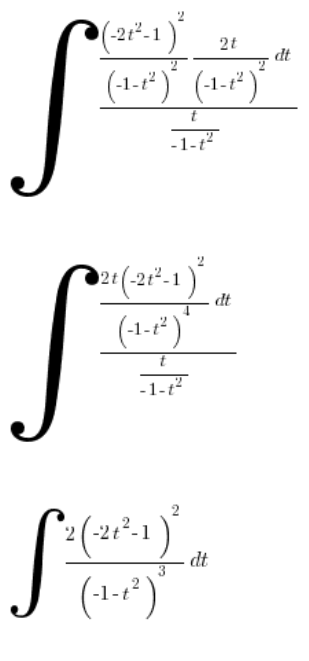
Wie erwartet, kommen wir auf ein wirklich komplexes rationales Integral, das ich nicht berechnen werde.

Schließlich ist es erwähnenswert, dass…

Hinweis zu Euler-Substitutionen

Wir haben ein Integral:

  ,

wo:

• Erste Art, wenn a>0
• Zweite Art, wenn c>0
• Dritte Art, wenn es zwei verschiedene Wurzeln gibt

Es ist offensichtlich, dass es oft mit einer der beiden Euler-Substitutionen oder sogar mit beliebigen von ihnen gelöst werden kann (wenn a>0, c>0 und gleichzeitig ).

Kein Problem, obwohl ich aus Gründen der Berechnungsfreundlichkeit empfehle, zuerst die erste Art zu verwenden, wenn das nicht geht, dann die zweite, und wenn das auch nicht geht, dann schließlich die dritte.

Das war’s zum Thema Euler-Substitutionen. Ich hoffe, es hilft euch im Studium weiter, und wie immer, fühlt euch frei, unten im Beitrag zu kommentieren.